蓝牙链路层加密算法—EO加密算法
不少人认为蓝牙的安全体系是产生问题的重灾区,会被任何稍有能力的投机者攻破。相反,另一些人则认为蓝牙的安全性已经足够好了。这其实取决于你想用蓝牙来做什么。对于普通用户而言,大部分信息都不值得花比信息本身更高的代价去破解。但如果要将蓝牙用于商业、金融业、军事业等来传输极具价值的信息,那么就有必要了解蓝牙的安全能力。下面我们就将具体分析一下蓝牙链路层所采用的加密算法EO的安全性。
一、EO加密算法简介
EO加密算法是蓝牙链路层的加密算法,属于流加密方式,即将数据流与密钥比特流进行异或运算。对每一分组的有效载荷的加密是单独进行的,它发生在循环冗余校验之后,前向纤错编码之前。主要原理是利用线性反馈移位寄存器产生伪随机序列,从而形成可用于加密的密钥流,然后将密钥流与要加密的数据流进行异或,实现加密。解密时把密文与同样的密钥流再异或一次就可得到明文。
关于EO加密算法如图1所示。
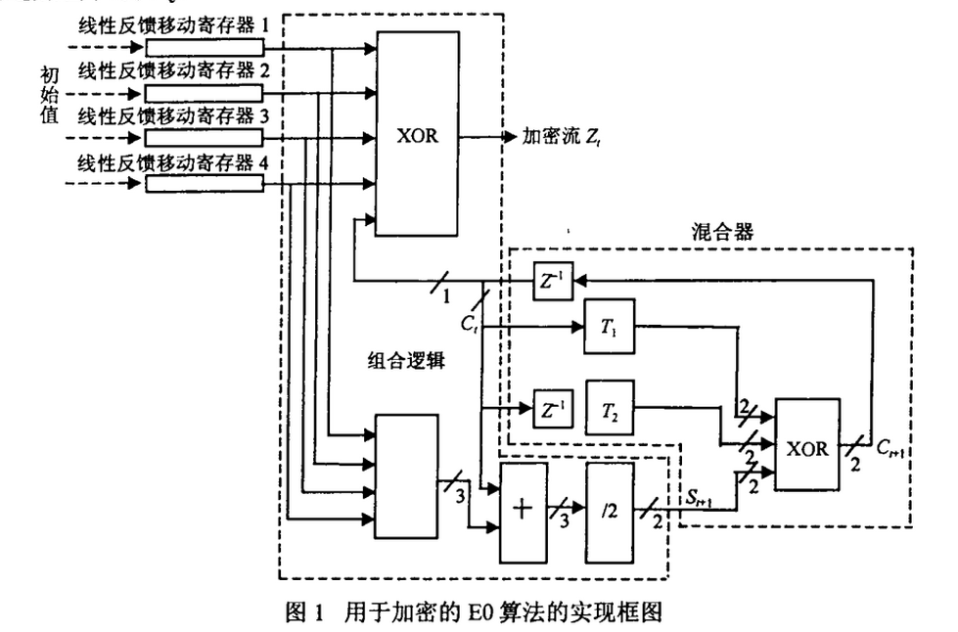
EO加密算法主要有:线性反馈移位寄存器组(Linear Feedback Shift Registcr,LFSR),(LFSR1~4)、组合逻辑和复合器(Blend)3部分组成,其中Blend中T1和T2为线性变换网络,Z-1为延迟网络。LFSRs的长度分别为25、31、33、39。采用多个LFSR是为了增加生成的伪随机序列的长度和随机性。当产生加密流时,LFSRs需要赋予初值(种子)。四个LFSR再加上各是两位的Ct和Ct+1共计132位,由主设备地址ADR(48位)、时钟CL(26位)和链路层加密私钥Kc(最多128位)提供,Kc由E3算法产生的。种子进入LFSRs的安排由图2给出。
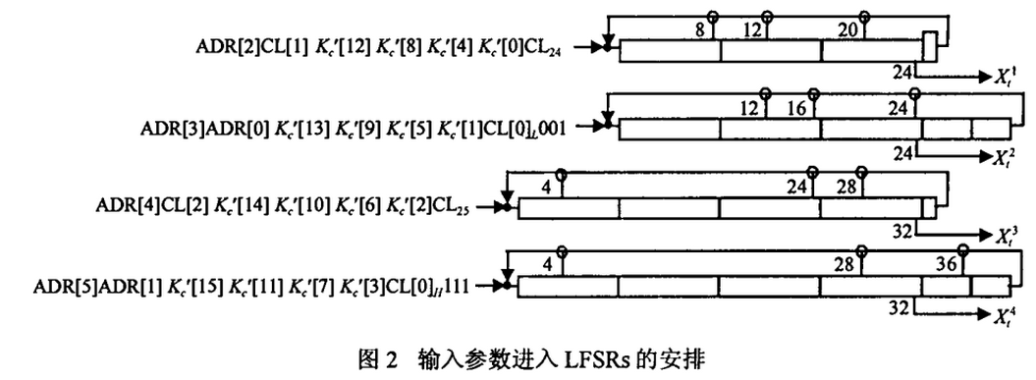
图中的材是由K变换得来。当LFSRs开始进行工作时,先产生的200位数据的后128位再次作为LFSRs的种子,而G和CI的值被保留,这时产生的伪随机序列就是加密所用的密钥比特流。之所以采用这样的两级加密是为了增加安全性,即使破解出第二级加密,也还必须破解第一级加密才能知道加密私钥Kc。
二、对EO加密流产生器的基本攻击
这种攻击是基于给定有限的(132位左右)输出加密流,重新导出LFSRs的初始值。输出的加密流可以通过某种方式获得的明文和密文按位异或得到。这种攻击对两级加密流的产生器都是有效的。攻击时,假定
已知Blend、LFSRI和LFSR2内容的初始设置,当已知输出的加密流时,虽不能输出LFSR3和LFSR4的确切值,但也能推导出LFSR3和LFSR4的异或值。由图l中得知在,时刻输出密流Zt为LFSRs的输出(即Xt1~Xt4)与C,O (Cr的低位)的异或结果。Xt3和Xr的异或值也可视作Xt3和Xt4的约束条件,把多位加密流得到的约束条件形成约束集,称为三。首先,把Z初始化为空。然后进行如下第一搜索,攻击算法的基本步骤为:
(1)设当前所测状态为f(开始时t=0)。计算Xt1. Xt1、Cto和zr的异或值,输出应和Xt3与Xt4的异或值一致。
(2)如果异或值为零,那么在三中加入约束条件Xt3、Xt4都为0或都为1。
(3)如果异或值为1,那么在L中加入约束条件Xt3≠Xt4。
(4)如果t≥33,那么在L中的约束条件含有LFSR3的反馈链。如果,t≥39,在三中的约束条件含有LFSR4的反馈链。在这两种情况下,如果新加入的约束条件与L中已有的约束相矛盾,这说明事先所做的关于Blend、LFSRI和LFSR2的假设不对,此时必须考虑假设其他情况。
(5)如果约束条件不矛盾,则计算Blcnd的次态。次态取决于现态和LFSRs输出1的个数。
(6)如果把t≥132,那么有很高的概率可以发现密流产生器的初始设置。如果不能,则继续搜索状态t+1。
该加密算法中有两点值得注意:先是Blend的次态取决于现态和LFSRs输出l的个数。因此,本文可以假定LFSR3和LFSR4不同而不需要知道哪个是0哪个是1,只要知道它们不同即可继续搜索。其次在约束条件集合E中的约束可以被有效的检测是否矛盾。
下面分析这种攻击手段的有效性。首先,考虑假设LFSR1、LFSR2的内容和Blend的状态都是正确。在任意t时刻,Xt3和Xt4的和(称为S)有两种情况:
(1)当Xt3和Xt4的异或值为1,s=1。Blend的次态Ct+1就已经决定了,因为次态只取决于现态和LFSRs输出1的个数。此时可直接进行Zt+1的分析。
(2)当Xt3和Xt4的异或值为0时,S∈{0,2}。 Blend的次态Ct+1要分别考虑s=o和s=2两种情况,此时需要分支考虑Zt+1。如果把对Z的分析看作结构树的根节点,以后的Z的位的分析,则可看作对结构树的分支。这个结构树的深度为33+39=72(即LFSR3和LFSR4的长度和)。由于对Z的每位,有一半的概率要分支,平均来看,对Z的每位平均分支0.5次,同时平均得到1.5个约束条件(无分支时有一个,分支时有两个),所以结构树的分支数为272/3=224枝,这数值也就是进行搜索的工作量。而最初假设的位数为60位(LFSRI和LFSR2共56位,Blend的现态和次态共4位),要得到正确的假定平均需要试259次,因此总的时间复杂度平均为0(239+24)=0(283)。这是基本的攻击方法,还可以利用一些特殊条件对攻击进行进一步的优化。
三、对EO密流生成器的优化攻击
为了优化攻击第二层密流生成器,如果LFSR3和LFSR4的异或输出有很高的汉明码重,那么攻击会更有效口为了利用这一点,本文通过假设扩展攻击,假设在一个密流的特殊点,LFSR3和LFSR4的异或为N
个连续的1(N33+39)。由于LFSR的输出在这个长度上随机且相互独立,在N+k个输出长度上产生这样一个序列的可能性为k.2-N(因为k<<2-N)。如果有的话,整个工作量将小于0(N.2(72-N)/3),同时明文的需要量不小于2N+132_N。因为当LFSR3和LFSR4的异或值为1时是不需要对结构树进行分支的。部分理论值由表1给出,同时给出了全部搜索所需要的次数。
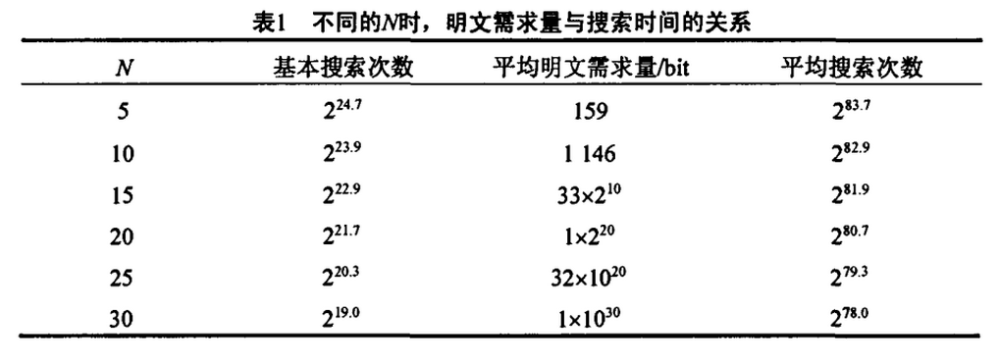
形式上,EO加密算法如下:
(1)在已知密流中选择132个连续的已知位;
(2)循环4位的Blender FSM、25位的LFSRI和最后的30-n位的LFSR2的状态;
(3)计算开始的LFSR2状态的n+1位,使得LFSR3和LFSR4的异或输出为一个1;
(4)在这一设置上运行基本攻击,如果发现恒定的初始值则停止。
以上算法将运行2的59-n次方次基本攻击,对一个单个的位置成功的可能性为2的-n次方,应当注意,即使是一个单个的数据包,其净荷长度最大为2745位,如果可以得到多个包的明文,就可以得到超过2 745位的密流。所有需要的下一步攻击是如何知道对任何一个包(Packet)来说,第二层密流产生器的初始设置。如果可能得到多个包,逐个去试它们,就能成功地找到任何一个包的初始设置。
四、对蓝牙EO加密算法的改进
根据以上的分析以及可能存在的攻击可以看出,EO加密算法的主要弱点在于图1中的yt信号是由LFSRs的输出位Xt1、Xt2、Xt3、Xt4简单的求和而得,当得知任何它们的异或结果很容易推出复合器的次态,以上的攻击手段都是在利用这一点进行的。因此可以针对这一点进行如下的改进,如图3所示,把简单的求和变成如图所示的算法。改进后的算法先对输出位Xt1、Xt2、Xt3、Xt4计数再求和,这时用以上所述的攻击手段不能奏效,因为求和的结果yt不仅与输出位xtl、Xt2、Xt3、Xt4的现态,也与它们的前态有关。改进后的EO加密算法具有以下优点:
(1)生成的加密流理论上更随机,原序列的长度最长为2的132次方-1,现在为最长可达2的144次方-1 。表2中所示的即改进前后数据的对比情况。

(2)无法进行以上所述的攻击手段,如果采用穷举法进行攻击,工作量比以前要大212倍,因为系统比以前多了12个状态。
(3)对原加密算法只做了很少的改动。一般为了速度等原因,加密算法主要部分都采用硬件实现,改进后的算法不需要改动算法软件部分的内容。
(4)改动的部分和原部分很容易进行某种使能方式切换,这样可以和原加密算法兼容。
EO加密算法是蓝牙链路层加密所采用的密流加密算法,它的安全性直接影响到整个系统的安全性。根据我们的分析,依据所获得的密文的长度,EO加密算法的安全性在78- 84位之间。在不改变基带的情况下,如果要提高蓝牙的安全性,只能采用公钥加密体制进行应用层的加强,例如椭圆曲线加密算法等。
小知识之基带
Baseband 信源(信息源,也称发终端)发出的没有经过调制(进行频谱搬移和变换)的原始电信号所固有的频带(频率带宽),称为基本频带,简称基带。











