基于RSA加密算法身份认证方案的设计

众所周知，计算机网络系统的安全性常取决于能否正确地验证通信或终端用户的个人身份。如机要部门或地区的进入、自动出纳机提款以及各种计算机资源系统的接入等都需要对用户的个人身份进行识别认可，为此，我们提出了一种基于RSA加密算法的身份认证方案。

一、 RSA加密体制及身份认证

由于计算机网络通信和各类应用业务的需求，要求相应的数据文件加密方法应具有灵活性和快速的特点。

RSA加密体制是1978年提出来的，它是第一个理论上最为成功的公开密钥加密体制，它的安全性基于数论中的Euler定理和计算复杂性理论中的下述论断：求两个大素数的乘积是很容易计算的，但要分解两个大素数的乘积，求出它们的素数因子却是非常困难的，它属于NP完全类，是一种幂模运算的加密体制。除了用于数据文件加密外，它还能用于数字签字和身份认证。要构造RSA加密算法和解密算法中的公钥和私钥，必须首先构造两个大素数，RSA加密算法和解密算法的安全性与所使用的大素数有密切关系。因此。研究RSA公钥加密体制中的大素数生成，构造符合RSA安全体系要求的强素数，是RSA加密算法算法实用化的基础。

身份认证可以防止非法人员进入系统，防止非法人员通过违法操作获取不正当利益、访问受控信息和恶意破坏系统数据完整性的情况发生。同时，在一些需要具有较高安全性的系统中，通过用户身份的唯一性，系统可以自动记录用户所做的操作，进行有效的核查。在一个有竞争和争斗的现实社会中，身份欺诈是不可避免的，因此常常需要证明个人的身份。通信和数据系统的安全性也取决于能否正确验证用户或终端的个人身份。对于计算机的访问和使用、安全地区的出入也都是以精确的身份验证为基础的。网络中的各种应用和计算机系统都需要身份认证来确认一个用户的合法性，然后确定这个用户的个人数据和特定权限。

二、 基于RSA加密算法身份认证方案的设计

1、 数字证书

数字证书建立在公开密钥和数字签名技术基础上，其主要作用是将持有人的身份与其公钥绑定在一起。数字证书由可信赖的而且独立的第三方认证中心(CA)颁发。证书的内容包括一个公开密钥、拥有该证书实体的身份信息以及CA中心对这些内容的数字签名，CA对数字证书的签名确保了该证书内容的完整性和真实性，CA不仅负责产生数字证书，而且承担对证书的管理、存档、发放以及作废等任务。基于公开密钥加密体制RSA的认证系统中，通信各方首先要获得数字证书，数字证书是通过管理仲裁机构建立的。

参加通信的所有各方事先自己生成一对密钥，将其中公开密钥部分作为申请书的一部分交给一个管理仲裁机构。仲裁机构对该用户及其公钥进行审查，认为其可以参加通信后，由该仲裁机构用自己的秘密密钥对一条信息进行数字签名，该信息包括该参加者的公开密钥和其他附加信息。仲裁机构将签名后的信息交给参加者，此信息就是证书(Certificate)。通信各方通过某种途径获得对方的数字证书后，用仲裁者的公开密钥验证证书的合法性，同时获得该用户的公开密钥。

2、用户间身份认证的设计思想

假设需要认证双方为A和B，A和B在通信前需要进行身份认证，以下是本文设计的身份认证思想。

（1）A将自己的身份IDA传递给B，但是B不能确定此信息是来自A还是窃密者C。

（2）B收到IDA后，产生一个随机的消息RB,用A的公钥PA加密IDA和RB得到y1=EPA(IDA+RB)，并用自己的私钥SB做y2=DSB(EPA(IDA+RB))运算即签名，将结果EPA(IDA+RB)和DSB(EPA(IDA+RB))传送给A。

（3）A收到消息后用B的公钥PB对DSB(EPA(IDA+RB))进行验证，验证原理是根据EPB(DSB(EPA(RB))=EPA(RB)。由于只有合法的B才拥有公钥SB，因此可以通过将计算结果与EPA(RB)比较，A就可以确认通信对方是否是B。如果验证通过，A就可以确认通信对方的确是B，并且对EPA(IDA+RB)进行解密，解密的原理是DSA(EPA(IDA+RB))=IDA+RB。通过解密得到IDA+RB，分离IDA和RB。

（4）A将求得的RB用B的公钥PB加密传送给B，因为只有合法的A可以求得RB从而可以得到正确的EPB(RB)；B只需用自己的私钥SB解密(EPB(RB))即可得到DSB(EPB(RB))=RB，将此RB与原来的RB对比就可以确认对方是否是A。

三、基于RSA加密算法身份认证方案的实现

为了实现信息的网络化管理，系统采用了VC.NET结合SQLServer2000数据库的解决方案，即将用户数字证书等有关信息存放在SQLServer数据库中。选用SQLServer2000作为后台数据库是因为该系统数据量大，系统的安全性较高，而且SQLServer2000在构造、部署和管理大中型的Web应用方面，有它独一无二的优点。利用VC.NET通过ADO.NET对学生选课数据库进行管理，ADO.NET是Mi2crosoft的数据访问框架，其核心采用了非连接数据的概念，而用于Internet通信的HTTP协议没有包含维护请求间状态机制，这样使得系统数据处理通过Internet进行非常顺利。

1、基于RSA加密算法身份认证方案的体系结构

系统采用了B/S(Browser/Server)三层体系结构，即表示层(Browser)、功能层(WebService)和数据服务层(DataBaseService)；IIS架设Web站点；VC.NET通过ADO.NET访问数据库。方案的体系结构图如图1所示。

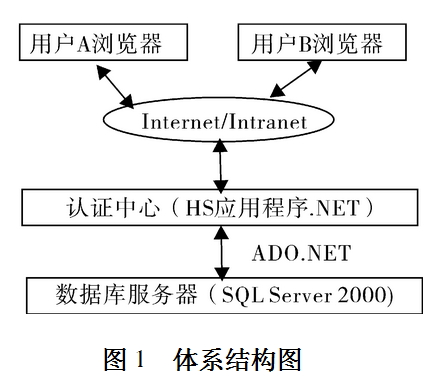
对数据库的访问在Web服务器端完成。客户端无须安装任何专门软件，通过浏览器即可访问Web服务器并运行其程序。采用了这种体系结构的系统充分利用了服务器资源，提供了跨平台、简单一致的应用环境，实现了开发环境与应用环境的分离，减少了系统开发和维护的工作量，便于用户群的扩展。

2、基于RSA加密算法身份认证方案的实现过程

（1）建立数字证书

选取两个大素数：p和q，并且两数的长度相等，以获取最大程度的安全性；计算两数的乘积：n=p3q；随机选取加密密钥d，为满足ed=1mod(p-1)(q-1)，则d=e-1mod((p-1)(q-1))，d和n也互素；e是公钥，d是私钥，n是公开的。两个素数p和q不再需要，可以被舍弃，但决不能泄露。这里我们假设生成了用户A的密钥对(eA,dA)和用户B的密钥对(eB,dB)。

用户将私钥d秘密保存，公钥e交给一个管理仲裁机构认证中心，获得自己的数字证书，然后将数字证书保存在自己的机器上，同时认证中心将合法用户的数字证书保存在数据库中，以便用户查询。用户当与网络上某个用户通信需要进行身份认证时，将自己的数字证书发送给通信的对方。对方收到数字证书后，首先通过认证中心验证其合法性。如果是合法的，就可以从证书中获得需要的用户公钥，然后利用该公钥验证对方的身份；如果不合法，就可以终止通信。

（2）进行身份认证

第一步：用户A对用户B的认证。

a、用户A发送自己的身份IDA传递给B。

b、加密：当用户B收到用户A的通信标识符后产生一个随机消息RB，用户B把用户A的标识符IDA和随机数RB组合在一起，构成明文m，然后把明文m进行分组。最后使用A的公钥利用加密公式Ci=meA
i(modn)，对每个分组mi进行加密。

c、签名：用户B用自己的私钥dB把加密后的消息Ci签名，公式为Si=CdBi(modn)，用户B把Ci和Si组合到一起组成C和S发给用户A。

d、验证：当用户A收到用户B发来的消息后首先对消息进行分离，分离出C和S，再将C和S分组为Ci和Si，用户A使用用户B的公钥eB对用户B的身份进行验证，验证公式为Vi=SeBi(modn)，如果Vi和
Ci完全相等，就可以说明对方就是用户B。

e、解密：用户A再使用自己的私钥dA对Ci进行解密，解密公式为mi=CdAi(modn)，然后把mi整合后，分离出用户A的标识符IDA′和随机数RB′，用户A把IDA′和自己的标识符IDA进行比较，如果相同则对方就是B。用户A对用户B的身份认证结束。

第二步：用户B对用户A的认证。

a、加密：用户A把RB′用用户B的公钥eB进行加密，加密公式为y3=EeB(RB′)，用户A把加密后的消息发送给用户B。

b、验证：当用户B收到消息后，使用自己的私钥对消息进行解密，解密公式为RB″=DdB(y3)。

由于RB是用户B产生的，如果RB″和RB相等，则说明对方就是用户A。用户B对用户A的认证过程结束。

认证过程如图2所示。

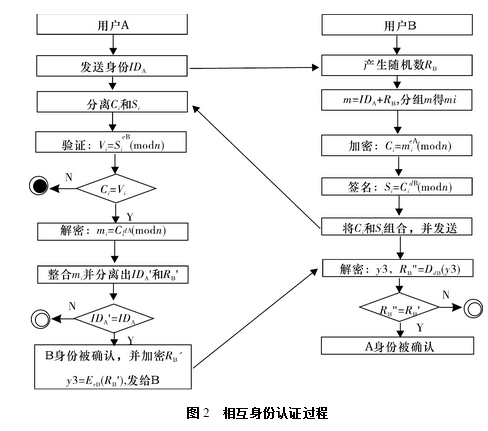
（3）基于RSA加密算法身份认证方案的实验

a、运行环境：硬件与网络环境:用服务器能运行WindowsXP、WindowsNT4.0+ServicePack6及以上操作系统，建议使用586或以上的计算机，并配有10M以上的网卡一块，如果采用电话线拨号上网的用户需要配置一台调制解调器。系统软件：操作系统Windows2000、XP及以上版本，SQLServer2000。运行环境：MicrosoftVisualC++6.0，浏览器使用IE5.5和MDAC2.6及以上版本。

b、代码实现

在认证过程使用的加密和解密算法相同，已利用VisualC++6.0实现，另外签名和验证的算法也和加密算法相同，只是每次利用的秘钥不同，这也是利用RSA加密算法进行认证的优势。这里只列出少数代码：

classCRsa{public:

{

CRsa();

intEncrypt(char3Out,char3In,UINTlen,char3KeyStr,char3ModStr);

//加密intDecrypt(char3Out,char3In,UINTlen,char3KeyStr,char3ModStr)//解密

{returnEncrypt(Out,In,len,KeyStr,ModStr);}

boolGetKey(BigInt&p,BigInt&q,BigInt&e,BigInt&d,BigInt&n,UINTplen,UINTqlen,UINTelen);

//获取RSA密钥对boolSetKey(char3KeyStr,char3ModStr);

//由输入密钥串设置RSA密钥和模nprivate:BigIntkey,n,Zero;

//密钥,模n,常量0

CBigIntBI;

};

intCRsa::Encrypt(char3Out,char3In,UINTlen,char3KeyStr,char3ModStr)

{

staticBigInta,c;

CHECK(Out&&In&&len&&SetKey(KeyStr,ModStr))//由输入构造一个大数a

CHECK_MSG(BI.BuildBIFromByte(a,In,len)&&a.len<=n.len,“错误:RSA加密(解密)的内容过长!”)//加密(解密)

CHECK(BI.PowMod(c,a,key,n))CGfL::HalfByteToByte(Out,c.bit,c.len);return(c.len+1)>>1;

}

本方案实现了一个基于RSA加密算法认证系统，其中RSA密钥长度最大可达600bits16进制数(约合720位10进制数)，而且产生RSA密钥对的速度非常快，一般在3s以内完成.在认证过程中，加密(签名)和解密(验证)时可以从文件中导入密钥，而且加密(签名)和解密(验证)速度也非常快，一般在6s以内完成。

admin普通用户

海报分享