椭圆曲线加密算法的C语言设计和实现

椭圆曲线加密算法于1985年提出，由于自身优点，它一出现便受到关注，现在密码学界普遍认为它将替代RSA加密算法成为通用的公钥加密算法。那么我们今天就来看看椭圆曲线加密算法是如何通过C语言来设计实现的。

一、椭圆曲线加密算法的C语言设计

1、椭圆曲线加密系统的基本结构

椭圆曲线的加解密流程如图1所示：

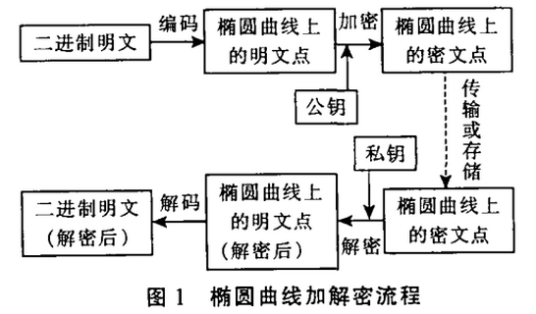
椭圆曲线进行加密通信的过程如下：首先选定一个适合加密的椭圆曲线Ep(a，b)，并取椭圆曲线上的一点作为基点G。选择一个私有密钥k，并生成公开密钥K=kG。加密时，将明文编码到Ep(a，b)上的一点M，并产生一个随机整数r(r<n)。

计算点C1=M+rK，C2=rGo将C1、C2存入密文。解密时，从密文中读出CI、C2，计算C1-kC2，根据C1-kC2=M+rK-k( rG)=M+rK-r( kG)=M，解得的结果就是点M，即明文。

2、高精度整数的表示

加密算法几乎都是建立在高精度大整数的运算上， 而一般的程序语言都不提供大整数的结构，因此要表示上百位的高精度整数需另辟蹊径。

本文使用了LibTomMath库的高精度整数结构。LibTomMath是一个计算高精度整数的库的开源软件，由加拿大人汤姆St.丹尼斯编写，用标准C语言写了几乎所有标准的密码算法模块，并且在几乎所有的操作系统下都可执行。

LibTomMath库对高精度大整数的表示是该库最大的一个特点。在LibTomMath库中的高精度大整数表示如下：在32位机上unsigned long为32bit，用mp_digit表示这个类型：typedef unsigned_long mp_digit；实际使用了32位的28位，少用4位，因此用16进制表示一个mp_digit为0XXXXXXX，其中X为16进制数字，将这个32位bit串称为一个mp_digit单元，若干个mp_digit单元构成一个大整数，结构定义一个大整数mpint如下：

typeclef struct {

inl used，alloc，sign；

mp_digit *dp;

) mp_int；

其中：dp是存放大整数的地址，将大整数（二进比特串）分段（mp_digit单元）存放在从该地址起的内存里，缺省时分配dp为MP_PREC=64个mp_digit单元，即alloc =64；used为实际使用的mp_digit单元；sign=0表示非负数，为1表示负数。对于分配了alloc个mp_digit的大整数mpjnL，因为实际可以使用的比特数是28*alloc，因此可以表示的整数范围是[-228*alloc，228*alloc]。对于64位机情况类似。

3、椭圆曲线的参数选取

在基于椭圆曲线的加密和解密实现方案中，首先要给出椭圆曲线域的参数来确定一条椭圆曲线。

在SECI及IEEE P1363ECC工作草案中，所定义的二进制域上椭圆曲线用到六个参量T=(p，a，b，G，n，h)o p，a，b用来确定一条椭圆曲线，G为基点，n为点G的阶，h是椭圆曲线上所有点的个数m与n相除的整数部分，这几个参量取值的选择直接影响加密的安全性。参量值一般要求满足以下几个条件：

a）p当然越大越安全，但越大，计算速度会变慢，200位左右可以满足一般安全要求；

b）p≠nxh；

c）pt≠l (mod n)，l≤t<20；

d）a3+27b2≠O (mod p)；

e）n为素数；

f）h≤4。

本文选用大素数域上的椭圆曲线E(p)：y2=x3+ax+b作为我们的加密曲线。

（1）参数a、b的选取

采用构造法产生椭圆曲线CM(Complex Multiplication)法，即先确定有限域Fp和其上的椭圆fHj线的阶，然后再构造满足要求的椭圆曲线，即求出椭圆曲线方程E(p)：y2=
x3+ax+b中的a，b。

（2）基点的确定

首先在椭圆曲线上随机选择一个有效点，然后根据选择的点得到阶是n的有效基点。这里有效基点的阶最好是曲线阶的点，至少是曲线阶的最大素因子，这样可以保证一定的安全。

（3）私钥的确定

随机选取1到P-1之间的素数作为私钥d。

（4）公钥的确定

由d乘我们所确定的基点得到公钥K，即K=dG。

4、椭圆曲线的点加和标量乘

对于一般的椭圆曲线方程yz+alxy+a3y =X3+a2xz+a,x+a6，设点P(xi，yl)，Q(X2，yz)的和R(X3，y3)的坐标为x3=k2+kal+a2+xl+x2；y3=k(XI-X4) -y1-alx4-a3，其中当P≠Q时（点加运算）k=（y1-y2）／（x1-x2）；

当P=Q时（倍点运算）k= (3x2+2a2x+a4-aly)/(2y+a1x+a3)；对于椭圆曲线方程y2-X3+aX+b，上述的公式变为X3=θ2_X1_X2; y3=θ(X1-X3) -y1，其中当P≠Q时（点加运算）θ=（y1-y2）／（x1-x2）；

当P=Q时（倍点运算）θ=（3x12一a）／2y1。

椭圆曲线中最基本最重要的运算之一就是标量乘法(ScalarM ultiplication)，即求点P的k倍。

在加密体制的实现中，它的运算速度直接影响到整体速度。目前计算标量乘的算法主要有二元展开法、带符号的二元法、k进制方法、带符号的k进制方法、滑动窗口法、Frobenius自同态法等。本文采用基本的二元展开法。表示如下：

设m的二进制表示为m=(mn-1mn-2…m1mo)，其中mn-1=1，Q=P，从左到右依次计算。

for(1=n-2 t0 0)

{

Q=2Q;

if(mi =1) Q=Q+P；

}

则Q=mP.

Return Q；

5、明文的嵌入和恢复

明文信息如何嵌入到椭圆曲线上也是椭圆曲线加密算法的关键之一。椭圆曲线一个点由x坐标和y坐标组成，因而一个点就是由两个数组成的数对，并且这两个数都要在椭圆曲线的有限域上。本文采用如下方法进行明文编码：

取一段明文作为椭圆曲线上点的X坐标，然后按照椭圆曲线方程yZ=X3+aX+b (modp)计算Y坐标的值，取明文的长度由有限域决定。若有限域长为192bit串，则取明文比特长应在1-191bit之间。由于本
系统高精度整数结构上处理的特点，需在取得的明文块后加结束标志字符char(255)，所以当有限域比特长为192位时，所取的最大明文块为22字符长。

由于本系统上的运算都是基于比特位的，且采用高精度整数结构，明文比特串和高精度整数之间需要一个转换过程。

（1）加密明文比特串的转换

mp_digit只用28比特，一个单元最多可存放三个半字节。

实现将明文文件的二进制比特串转换成mp_int数a的函数，主要循环部分说明如下：

//chlong为要存人的字符数组长

for (j=O;j<chlong/7;j++)//以7个字符为单元循环，

把7个字符放人mp_int的两个单元中

{

j+=-7；//每次跳7个字符

*++templ=(mp_digit) (ch [i-l]＆255);//Aemp

跳过前一个单元，存人后一单元

*temp<<=(mp_digit)CHAR_BIT;

//存人高8位并向左移8位，以便放人下一个字符

*temp 1=(mp_digit)(ch[i-2]&255);

//存入字符

*temp <<= (mp_digit)CHAR_BIT;

//左移8位

*temp I-(mp_digit)(ch[i-3]&255);

//存人字符

*temp<<-(mp_digit)4;//向左移4位，以便放入下一个字符的高4位

*temp-1.(mp_digit)((ch[i-4]&255)>> 4)；

//存放被切分的字符的高4位，temp跳回前一个单元

//存人第一单元

*temp f- (mp_digit) (ch[i-4] &)7);

//存放被切分的字符的低4位，yy= (mp._digit) 15

*Lemp<<．(mp_digit)CHAR_BIT;//向左移8位，以便放人下一个字符

*temp I-(mp_digit) (ch[i-5]＆255);11存入字符

*temp<<：(mp_digit)CHAR_BIT;//左移8位

*temp J=(mp_digit)(ch[j-6]&255)：//存人字符

*temp<<=(mp_digit)CHAR_BIT;//左移8位

*temp++|=(mp_digit)(ch[i-7]＆255)；//存放被切分的字符的低4位．temp跳到后一个单元

temp++；//再向后跳一单元，这样和下次的++temp实现每次循环跳两个单元

}

明文恢复时，采用和上面相反的过程将mp_int数转换成明文的二迸制比特串。

（2）密文的存储结构

在文件加密存储中，需解决密文存入磁盘后如何读入和区分每次加密的密文段的问题。本文是如下处理的：

存储时先存*mp->dp的最高8位，再依次往下存后面3个8位。依据*mp->dp的特点，最高8位为0000xxxx，因此，可将255作为一个密文段的结束标志，把前一密文段和后一密文段区分开。这样在密文文件中，密文的存取结构为：

用变量i记数，利用fgetc每次读取一个字符，当第i个字符是255，且i%4=0时截止。这时所读的这段字符即为一次存储的密文段。读出密文段后，用相应的方法把密文段比特串转换成mp_int型数。

二、椭圆曲线加密算法的C语言实现

文件加密、解密处理都是根据有限域大小分段进行的。加密时无论明文文件的表现形式和内容如何，都将其组成成分看作是二进制数字文件。

文件加密时，每次取一段二进制明文，并在末尾附加一个明文结束标志字符char(255)，以避免二进制的明文读入mpjnt数后出现高位比特位是0，导致出错。取得明文后，产生一个随机整数r(r<有限域p），计算点C1=M+rK、C2=rG，将点C1、C2坐标依次存入密文文件。

文件解密时，按前述方法读入密文。根据C1-dC2=M+rK-k (rG)=M+rK-r(kG)=M计算C1-dC2（d为私钥），得到明文点坐标mx，myo其中两点减的计算为P-Q=P+(-Q)，其中-Q=(X，-Y)，-Y=P-Y；计算C1-dC2完毕后按前面所述取解密文的方法取出解密字符，去掉最末的一个char(255)符，存入解密文中，完成解密。

为验证系统的文件加密、解密功能，我们对文本文件、BMP、WORD、EXCEL等文件进行了加密和解密测试。验证结果表明，所给定的明文文件经系统加密后，再对密文解密所得的解密文与原明文相比完全一致，没有一个比特的偏差，很好的实现了椭圆曲线加密算法的功能。

admin普通用户

海报分享