admin 非对称加密体制（也称作公钥加密体制）于1976年提出，他不同于以往的加密算法，非对称加密技术的思想不是建立在位方式的操作之上，而是建立在数学函数的基础之上的。更重要的是，与只使用单一密钥的传统加密技术相比，每一个通信方都拥有一对密钥，其一公钥是可以公开的，其二私钥是保密的，只有自己才知道。在进行加密时，加密方使用对方的公钥，而解密时使用自己的私钥进行解密，这样就保证只有私钥持有者才能进行解密。那么我们今天就来给大家介绍一下非对称加密体制中的典型算法——RSA加密算法。
一、非对称加密体制的思想
非对称加密体制必须满足以下条件：
1、公钥和私钥之间具有紧密的联系，即公钥和私钥源自同一数学推导关系。
2、用公钥加密的信息只能由相应的私钥进行解密，反之亦然。而由公钥推知私钥，在计算上是不可能的。
利用非对称加密方案进行通信的过程是：
发送方A先查找接收方B的公钥，因为公开公钥并不影响通信的保密性，B可以将自己的公钥公布在公共数据中，然后，A采用公钥加密算法用B的公钥对原始信息进行加密，并通过非安全信道将密文发送给B。当B接收到密文后，通过自己持有的私钥对密文进行解密而还原出明文。在这种情况下有：
E(K1,M)=C
D(K2,C)=M
D[K2,E(KI,M)]=M
其中，K1为加密密钥，K2为解密密钥，C为密文，M为明文，E为加密算法，D为解密算法。
二、RSA加密算法
非对称加密体制只是一种思想，1978年有专家又提出了一个基于数论的非对称密码体制。它是一种分组加密体制。实现该加密体制的核心是RSA加密算法，其名称来自于3个发明者的姓名首字母。为提高保密强度，RSA密钥至少为500位长，一般推荐使用1 024位。非对称加密技术的安全性是基于大整数因子分解的困难性，而大整数因子分解问题是数学上的著名难愿，至今没有有效的方法予以解决，因此可以确保RSA加密算法的安全性。
1、RSA加密算法需要以下相关的数学概念：
素数：素数是比1大，其因子只有1和它本身，没有其他效可以整除它的效，素数是无限的，例如2，3，5，7……等。
两个数互为素数：指的是它们除了1之外没有共同的因子，也可以说这两个数的最大公因子是1。例如，4和9，13和27等。
模运算：如A模N运算，它给出了A的余数，余数是从0到N-1的某个整数，这种运算称为模运算。
2、RSA加密算法流程：
1）先找出一对足够大的、不同的素数p和q。
2）计算公开的模数r=pqg。
3）计算欧拉函数φ(r)=(p-1)(q-1)，两个素数p和q不再需要，应该丢弃，不要让任何人知道。
4）找一个与φ(r)互质的数e，且1<e<φ(r)，整效e即为加密密钥。
5）计算d，满足de≡1(modq, φ((r))，d为解密密钥，要保密。
公式中，“≡”是数论中表示同余的符号，符号≡的左边必须和符号右边同余，也就是两边作模运算的结果相同。很显然，无论φ(r)取什么值，符号右边1modφ(r)的结果都等于1；符号左边d与e的乘积作模运算后的结果也必须等于1，这就需要计算d的值，让同余等式可以成立。
6）将明文x（其值的范围在0到r-1之间）按模为r自乘e次幂以完成加密操作，从而产生密文y（其值也在0到r-1范围内）
y=xe(mod r)
7）将密文y按模为r自乘d次幂，完成解密操作。
x=yd(mod r）
由于RSA加密算法的公钥和私钥的长度（模长度）要达到1 024甚至2 048方可保证安全，因此，p、g、e的选取、公钥与私钥的生成、加密解密模指数运算都需要一定的计算机程序才能完成。
三、RSA算法的安全性
在RSA密码应用中，公钥K1是公开的，即e和r的值可以被第三方窃听到，破解RSA密码的问题就是从已知的e和r的值想办法求出d的值，这样就可以得到私钥来破解密文。
从RSA加密算法可以看出，密码破解的实质是从p、q的值，求出(p-1)和(q-1)，也就是只要求出P、q的值，就能得到d的值而得到私钥。但当P、q是大素数的时候，从二者的乘积去分解因子P、q，这是—个公认的数学难题。比如当P、q大到1024 bit时，目前还没有人可以利用任何计算工具完成这一分解任务，因此RSA加密算法经受住了各种攻击的考验，逐渐为人们所接受，被认为目前最优秀的公钥方案之一。
其他的安全问题包括：
1）公共模数攻击
每个人具有相同的，但有不同的指数e和d，这是不安全的。
2）低加密指数攻击
如果选择了较低的e值，虽然可以加快计算速度，但存在不安全性。
3）低解密指数攻击
如果选择了较低的d值，这是不安全的。
4）选择密文攻击
如A想让T对一个T不愿意签名的消息m’签名．A首先选择一个任意值x，计算y=xe(mod r)，然后要求T对m=ym’签名，A最后计算(momod r)d modr =(ym’)dx-1modr=m'd mod r。因此一般不要对别人提交的随机消息进行签名。
四、RSA加密算法的缺点
由于进行的都是大数计算，使得RSA最快的情况也比DES慢几倍，无论是软件还是硬件实现。速度一直是RSA的缺陷。
此外，RSA加密算法产生密钥的过程很麻烦，受到素效生成技术的限制，因此很难做到一次一密。分组长度太大，为保证达到安全性。r至少耍有600 bit，使运算的的代价很高。一般来说RSA加密算法只用于少量数据文件加密。为了解决速度问题，目前人们广泛使用对称加密和非对称加密结合使用的方法，这样，RSA与DES的优缺点正好互补。RSA的密钥很长，加密速度慢.。而采用DES，正好弥补了RSA的缺点。即DES用于明文文件加密，RSA用于DES密钥的加密。由于DES加密速度快，适合加密较长的报文；而RSA可解决DES密钥分配的问题。美国的保密增强邮件(PEM)就是采用了RSA和DES结合的方法，目前已成为E-MAIL保密通信标准。
加密领域的实际应用要求远比单一使用某一种加密算法复杂，因此，多种加密算法综合使用，取长补短，才能达到更好的保障数据的安全之目的。
小知识之欧拉函数
欧拉函数实际上是模n的同余类所构成的乘法群（即环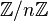
的所有单位元组成的乘法群）的阶。这个性质与拉格朗日定理一起构成了欧拉定理的证明。
