一种自适应综合DCT系数置乱加密算法
在压缩编码过程中加密敏感数据,常用的是加密DCT系数,称其为DCT系数加密算法,其中,加密过程位于压缩编码过程之中,DCT系数加密算法还存在很大的发展空间,具有较大的潜力尚待挖掘,因而成为当前乃至以后的研究热点。
一、DCT系数加密算法
1、DCT系数加密算法
DCT系数加密算法主要包括t频度域鼍乱算法、Zig -Zag置乱算法、分段Zig - Zag置乱算法和符号加密算法。
DCT系数加密算法的计算复杂度和差错扩散性两方面的性能都很优越。然丽这3种算法在可靠性和对压缩比的影响方面,DCT系数加密算法存在着较大的不足,这也是DCT系数加密算法不能被广泛接受的主要原因。
2、自适应综合DCT系数置乱加密算法
自适应综合DCT系数置乱加密算法(以下简称“综合加密算法)结合了频度域置乱算法和分段Zig - Zag置乱算法的特性,充分利用了这两种算法的优点,摒弃了各自的不足,使得这两种处理方法间优势互补。
综合加密算法将加密处理过程置于1帧的帧内预测之后,加密的是差分DCT系数,是一种分组加密算法,他将欲加密的对象(即1帧图像)先分成一定长度的许多组,每次只对其中的一组进行处理。在同一个8×8数据块中,DCT系数块按图1进行划分。
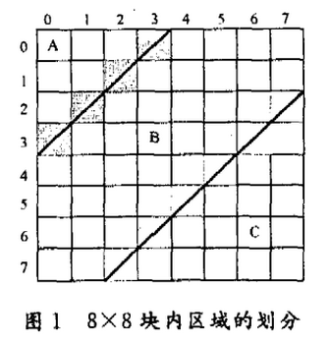
该DCT系数块被两条斜线分隔成A,B和C三个区域,对A区的系数进行频度域置乱加密,对B区中的系数进行Zig - Zag置乱加密,对于每个8×8块内部的区域划分在不同的组内是不一样的,即图1的分界线的位置是相应可调的。这也正是综合加密算法的独特之处。关于块内的区域划分策略(即各条分界线位置的确定)在后面将详述。
为了增加算法的可靠性,必须使每一次加密的密钥是不同的,因而,这要求加解密双方都应存有一份相同的密钥库,并根据一定的方法从中取出相同的密钥。
二、综合加密算法
1、加密组长度
加密组长度按既定的模式进行变化,比如,通过查表获取等。原则上说,图像所能包含的宏块总数(设值为n)即为加密组长度的上限。然而,若整帧图像只包含一个加密组,则加密强度就不会很高,原因是所有B区的系数就只用到一个加密密钥。若把上限值设为n-1显然也不行,因为当一个加密组的长度正好取为n-1时,另一个加密组的长度就只能为1 。随图像的复杂度和帧的类型的不同,这个值也有所不同。根据对多种类型视频图像的观察分析,综合加密算法将这个下限值设定为5(对于此值的准确性目前没有统计数据支持,有待进一步确认>。以此为根据,对于不同类型图像的加密组的长度上限就应为
n-5。然而,对于4GIF图像,n-5=1.579。当一个加密组的长度接近该值时,由于需要缓冲,会占用较大的存储空间,同时也会带来较大的编码迟延。因而,在不对算法的可靠性造成影响的前提下,规定所有加密组的长度不得超过255。采用255作为加密组长度上限,除了是从算法计算复杂度的角度考虑外,还因为这个值只需1个字节就能存放,从而减小相应的加密参数表所占的存储器空间。
在某一个确定的帧内,加密组的长度值是通过查表获得的。因此,对于不同的分辨率、不同的帧类型存在对应的加密组长度表。帧中加密组的序号和表中的每一个表项一一对应。很显然,为了保证加密组长度的限制,这些表项需经过专门的设计。为了保证各帧之间加密组划分的可变性,必须为该类型的帧提供多个不同的查找表,以进行轮换使用。通过权衡查找表对存储器空间的占用和算法的可靠性,综合加密算法规定为每一类型的帧提供50个不同的查找表。当然,由于B帧的出现频率最高,查找表重复利用的频率也就最高。但B帧携带的信息量是最少的,从对单位信息量的加密强度考虑,各类型帧之间相差不大。
综合加密算法采用的是加密组元素位置固定策略。并且同组元素也不是遍及整个帧的零散分布的宏块,而是采用相邻宏块组成同一个加密组。因为差分DCT系数在相邻宏块之间不具有相关性。
2、块内加密区域的划分
如图1所示,第1条和第2条分界线将整个8×8的块分成3个部分:A区、B区和C区。综合加密算法对这3个区的DCT系数分别对待:对A区进行频度域置乱处理,对B区进行Zig - Zag置乱处理,对C区的系数不做处理。综合加密算法除了对A,B区的系数进行了相应的加密处理以外,对C区的系数和P帧、B帧的运动向量都未进行加密处理。在频率域,不同频度的系数是不相关的,因而C区的系数同A区和B区不相关,攻击者不能从C区的系数中得到任何对破解加密数据有用的信息。对B区进行频度域置乱会使最终的编码数据量大幅增加,其原因是参与加密的块的DCT系数分布在B区的差异性最大。然而在同一块内对B区的Zig - Zag置乱对最终生成的编码数据量的影响是不定的,经过平均后,总体上对压缩比不会产生影响。因而,B区的最佳位置应该是加密组中各块的DCT系数分布差异最大的区域。通过对同组中所有块的全部DCT系数进行比较,可以找到B区的最佳位置。然而这种比较的计算盘是巨大的,对于实时视频传输应用领域,对处理器的计算能力的要求会很高。若对各块间DCT系数分布差异进行更深入的分析,可以找到另一种相对较简单的划分策略。我们对加密过程进行了模拟,并对图2各块间DCT系数的分布差异进行了统计。
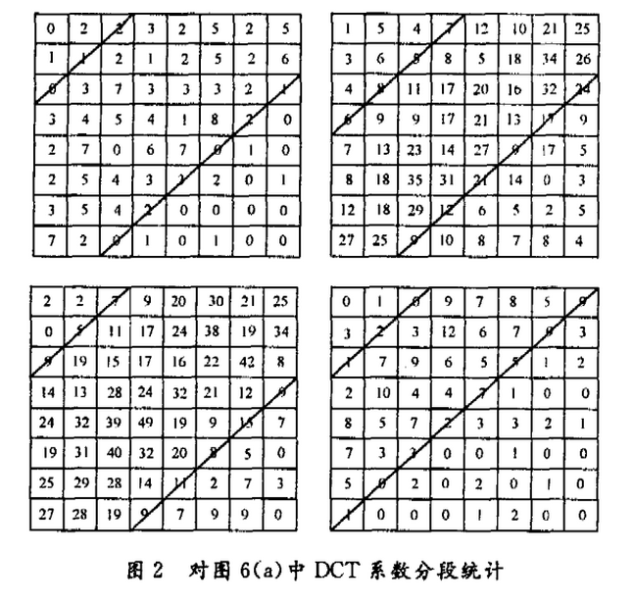
统计操作的过程如下:
(1)每个加密组长度的确定。将1~64的序号写在64张纸片上,并通过随机抽取的方式获得一组数字(共4个):9,43,55,15。
(2)每个加密组首宏块位置的确定。将1— 300的序号写在300张纸片上,并通过随机抽取的方式获得一组数字(共4个):127,256,204,49。例如,图6(a)的宏块总数为320,考虑到加密组本身的长度,因而将首宏块的位置人为限制在300范围内,这并不会对统计产生较大影响。
(3)在获得的每个加密组中,以首宏块为标准,在其后的每一个宏块中,凡是其同频系数是否为零的情况与首宏块不符合的,就使该频度处的值加1。
统计结果如图2所示,这里只罗列了宏块的第3个亮度块的情况,图中已经表明了3个区域的划分。可见,这4对分界线标号的平均比值约为4,即近似满足式(1)的关系,式中a和b分别是第1条分界线和第2条分界线的标号。图中分界线的标号定义为所在位置处的DCT系数的2个脚标的和,如图1所示,比如,左上角的那条分界线(简称为第1条分界线)的标号为3,右下角的那条(简称为第2条分界线)的标号为9。
![]()
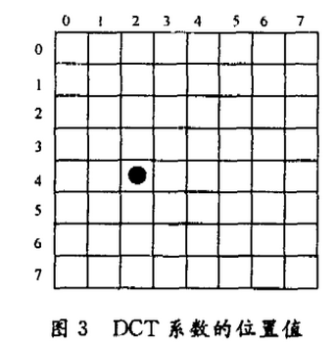
因此,只要求出第1条分界线的位置,就可以推出第2条分界线的位置。找到每个8×8块的最后一个DCT系数,所谓“最后”,是指按Zig - Zag排序后处在1×64序列的最后一个非零系数。计算并记录该系数的位置值,这个值等于该系数在原8×8块中的两个脚标的和,比如在图3中,黑点系数的位置值为6。求出加密组内所有最后DCT系数的位置值的平均值,将该值作为第2条分界线的标号。
2、加密参数的传递
采用综合加密算法进行加解密的双方必须使以下参数保持一致,才能正常运行:密钥、各加密组的长度、块内第2条分界线的标号。对于密钥,由于加解密双方都保存着相同的密钥表,并且按照某种规律从中提取密钥。因而,在加解密过程中是不需要传递密钥的。对于各加密组的长度,和密钥一样,加解密双方可按照相同的算法来确定整个视频序列中每一个加密组的长度值。但和密钥不同的是,这里存在一个同步的问题。在一个视频序列中,若某个宏块丢失,将会导致其后所有加密组的错位,从而在解密时就失去同步。值得庆幸的是,在当前的所有压缩编码标准中,对压缩后的宏块都有一个标号,解密方就可以利用这个标号来实现同步,而不是根据实际接收到的宏块个数来确定加密组的起始位置。因而,加密组的长度参数在加解密双方是不需要传递的。对于块内第2条分界线的标号,是根据加密组DCT系数的分布情况计算出来的,是根据图像的内容自适应更改的。斛密方不可能事先知道第2条分界线的标号,也不能够从加密后的DCT系数中计算得到。因而,这是必须通过传递才能告知解密方的参数。当知道a值就能够求出b值,且一般情况下a<b,因而传递第1条分界线的标号比传递第2条分界线的标号要更为合理些,这可使对应的Huffman码字较短。
因此,在综合加密算法中,传递的是第1条分界线的标号。
3、密 钥
对于每一次加密计算,都需从密钥表中获得对应的密钥,这是一个对存储器的访问过程,通常会占用一个总线周期。确定加密组长度的过程也是一个查找过程。因而,若这两种参数通过一次查找就可全部获得,则可以减少一次对存储器的访问开销。要达到这一目的是很简单的,只要将这两个参数放置在查找表的同一个表项中即可。然而,在一个视频流中,同类型帧的加密组长度与加密组序号之间的对应关系每50帧就重复一次,这将导致所使用的密钥也会每50帧重复一次。若欲使密钥与加密组长度之间不具有这样的绑定关系,即对于每一个加密组,密钥是可任意选择的,那么,就必须对密钥单独进行一次存储
器的访问,并为所有的加密组单独生成密钥表项。欲使密钥使用的重复频率低予每50帧一次,则表项的总量将是巨大的。因此,为不增加算法的计算复杂度和对存储器的访问次数,综合加密算法将密钥与加密组长度绑定在一起,存放在查找表的同一个表项中。
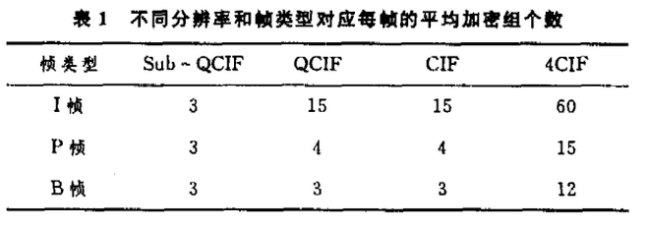
每帧的平均加密组个数,如表1所示。每个宏块共有6个小块,50帧内包含的加密组的总和为7 000。密钥空间为42 000。这个值可用16比特的二进制,即2个字节表示。
4、分界线标号在加密组中位置
由于加密组的最大长度为255,因而分界线标号在加密组中位置只需用1个字节来表示。为了增加对该参数传输可靠性,需采用一数多传的策略。是否需要对每一个放置该参数的位置都分别表示呢?其实,没有这个必要。因为隐藏分界线标号所放位置的目的,是为了避免加密组同步信息的暴露。只要这个放置位置在不同的加密组之间是变化的,则同一加密组中一数多传的各个参数间的位置是否具有相对的变化是不重要的‘们。综合加密算法规定:对每个分界线标号在加密组中的位置参数只传2次,中间间隔2个宏块,只标出第一个放置的位置。
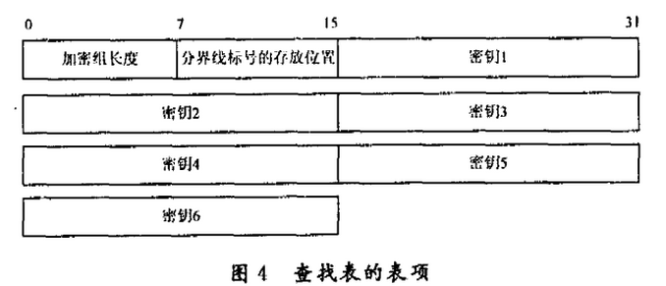
分界线标号的放置位置同样是通过查找的方式获得的。由于该参数是和加密组一一对应的,因而可以同加密组长度参数和加密密钥共同存于一个表项中。这样,通过对存储器的一次访问,就可将3个参赛全部取出。图4表示的是查找表表项中3个参数的存放情况。
5、DCT系数的置乱处理过程
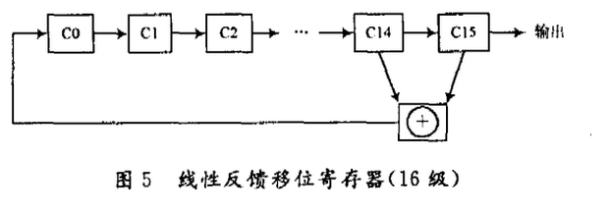
综合加密算法采用线性反馈移位寄存器作为随机序列发生器,图5所示的是16级移位寄存器。假设在加密处理以前,已经获得了足够大的缓冲区,缓冲区的结构和加密组的结构一样,也是由宏块组成的,只不过这些块内没有数据。对于长度为俺,B区DCT系数为m个的加密组。其置乱处理过程如下:
(1)将16位的密钥送人移位寄存器。
(2)先进行16次移位操作。
(3)其后每移位一次就进行如下操作;
①将最新输出的log2n位数据(设为x)和n比较,若x≤n,则将加密组内第x块的A区系数从该加密组剔除。并存入缓冲区中块号最小的空块内,同时加密组的长度减1,即n= n-1,若x>n,不做处理。
②将最新输出的log2m位数据(设为y)和m比较,若y≤m,则将加密组所有B区的第y个系数从B区剔除,并存人缓冲区相应各块的B区中序号最小的空位置处,同时加密组的长度减1,即m=m-1,若y>m,不做处理。
(4)以上循环满足以下任一条件就结束:
(a)所有块的A区系数和所有的B区系数都被移入缓冲区。
(b)移位次数(不包括最开始的16次)为疗和拼中最大值的3倍,即3×max(n,m)。
当循环是根据b条件结束的,则将原加密组中剩下的部分数据按顺序存入缓冲区的剩余空间内。
(5)将缓冲区的全部系数移回加密组。
三、加密算法的实验结果
由于加密所需的参数查找表制作的工作量非常大,利用该表的目的只是为了增加加密的可靠性,由于在算法的可靠性方面目前还不具备实验的条件,所以,实验采用的是一个近似的简化算法。该简化算法在对图像加密后的效果方面和对压缩比的影响方面和原综合加密算法是一样的。该简化算法只用了一个16 b的伪随机二进制码作为密钥,每个加密组的长度固定为16个宏块。
1、加密效果
对图6(a)采用简化的综合加密方法进行处理,得到的效果如图6(b)所示,将该图与原来的用两种算法得到的图像分别进行比较,发现综合加密算法的加密效果比频度域置乱算法要好,和全Zig - Zag置乱算法的加密效果相当。
另外,由于综合加密算法对绝大多数的DCT系数进行了文件加密处理,采用简单的过滤方式对加密后的图像进行处理是无法恢复原图像信息的。比如,将图6(b)中加密了的全部DCT系数屏蔽掉(即全部置零)后得到的图像几乎完全不可恢复,如图6(c)。不像频度域加密那样,某些高频信息清晰可见。由于图6(b)中未加密的高频系数太少,所携带的信息的能量太小,不仔细观察,几乎不能感知其存在。

2、 对压缩比的影响
在不进行加密处理的情况下,对图6(a)进行压缩后得到的数据量为26703 B,采用简化算法后得到的压缩数据为29906 B。可见,该算法使得压缩比有所下降,下降幅度为12%。和分段Zig - Zag置乱算法使压缩比下降的幅度15%相比,综合加密算法略有优势,但比全Zig - Zag置乱算法和频度域置乱算法的性能要高许多。
小知识之DCTDCT又称离散余弦变换,是一种与傅立叶变换紧密相关的数学运算。在傅立叶级数展开式中,如果被展开的函数是实偶函数,那么其傅立叶级数中只包含余弦项,再将其离散化可导出余弦变换,因此称之为离散余弦变换。











