双向耦合映像格子模型的图像加密方法
目前,基于低维混沌系统的应用于图像文件加密已十分普遍,但低维混沌系统在有限精度下存在短周期的缺点成为在实际应用中最大的障碍,但是低维混沌系统的实现简单、运算速度快等特点使得它们仍不能被抛弃。为此,研究具有高自由度和高复杂度的时空混沌系统并应用于图像加密迫在眉睫。我们提出了双向耦合映像格子模型的图像加密算法。
一、双向耦合映像格子模型
时空耦合映像格子是一个时间空间离散化,但状态变量仍保持连续的动力学系统。耦合映像格子有着相对简单、容易计算等特点,被广泛应用于时空混沌控制、同步、保密通信等研究之中。
描述时空混沌系统的主要数学工具有耦合常微分方程、偏微分方程、耦合映像格子模型等方程,其中耦合映像格子模型(CoupledMapLattice,CML)是研究人员经常使用的研究工具。本文加密算法中用到的是双向耦合映像格子模型(TwowayCoupledMapLattice,TCML)。
TCML模型的定义:
![]()
式中,其中f(_)为非线性映射,ε为耦合系数,周期性边界条件满足xn(0)=xn(L),xn(i)∈(0,1)。n=0,1,......为时间方向上的变量,i=0,1,......,L-1为空间方向上的变量,L为系统尺寸,函数f(x)取为Logistic混沌映射:
![]()
其中3.5699456...≤μ≤4,0<xn<1。
二、TCML混沌序列的产生及改进
良好的混沌图像加密系统必须具有优良相关特性的序列。用TCML模型生成三路混沌序列{b(0),b(1),b(2)}的过程如下:
(1)参数选择:对式(1)中的双向耦合映像格子模型,以Chebyshev映射产生的0到1之间的均匀分布的随机数为初始值。系统尺寸L=30,迭代过渡过程长度len=2000;系统迭代次数N=5000;Logistic映射参数μ=4,耦合系数ζ=0.234。
(2)系统格子初值产生:对式(3)Chebyshev映射取初值x0迭代2000次,得到x2000,继续迭代,判断此时xn值是否落入区间(0,1)。若是,将xn作为格子0的初值;否则,继续迭代,直到xn落入区间(0,1)。重复上述步骤,直到30个格子都取得驱动初值。
![]()
(3)TCML序列产生:将步骤(2)中得到的系统格子初值,代入满足步骤(1)中参数的TCML系统迭代N次,去掉len长度的过渡过程,格子9、18、27的后N-len点分别作为三路混沌序列{b[0],b[1],b[2]}。
对{b[0],b[1],b[2]}求序列各自的序列密度分布(量化到[0,255])、自相关特性和互相关特性来检测序列的密码学特性如图1所示。
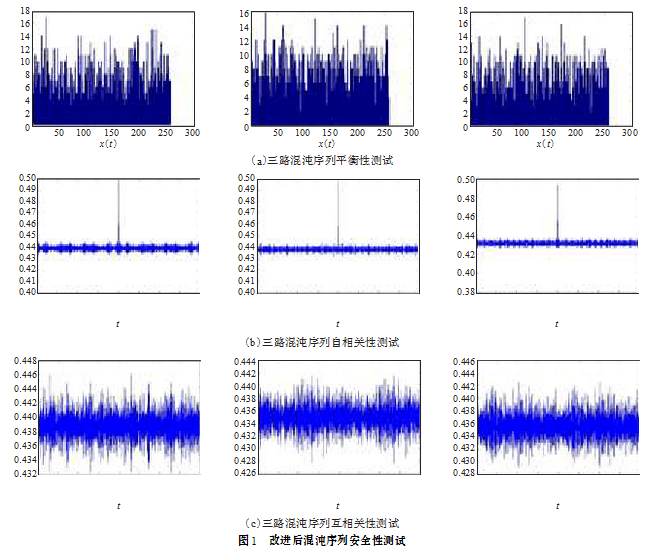
可以看到各路序列密度分布较差,如果直接用这样的序列对图像进行加密,密文很容易被攻击者破译。为了达到均匀分布的目的,采用一种改进的混沌序列生成方法对直接得到的混沌值进行预处理。整个预处理过程可由下式实现。
![]()
其具体思路是,将某格点上的状态量与其某相邻格点的状态量相减,得到的值作为新格点的状态值,改进后的各个序列密度分布、自相关特性和互相关特性如图1所示。
(4)对混沌序列{b[0],b[1],b[2]}进行改进,完成混沌序列生成。
三、图像加密系统设计
1、加密系统密钥设计
加密系统的密钥分为用户密钥和图像密钥两部分,其中用户密钥是由用户提供的,由3个字节组成,记为key1、key2、key3;图像密钥是根据具体明文图像内容提取出来的密钥:任
意选取4个不同的图像密钥。这里为了方便,从原始图像f中任取6个像素点,每两个像素点一对,按比特位进行异或操作,得到3个8位的辅助密钥ka,kb,kc。为了提高系统的明文扩散能力和明文敏感性,混沌参数选取规则如下:
(1)系统尺寸L=30;
(2)Chebyshev映射参数:
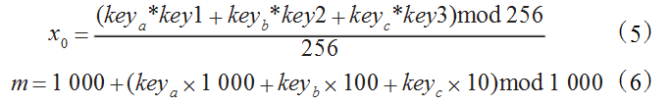
以x0为初值将Chebyshev映射迭代m次,按上章的有关步骤生成初始序列{init(i)(i=0,1,.....,29)};
(3)TCML系统参数
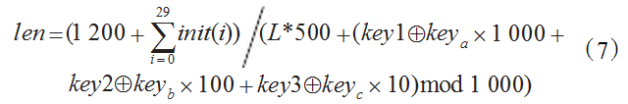
2、加密过程
(1)将TCML系统在初始序列{init(i)(i=0,1,.......,29)}作用下迭代len次,得到新序列{s_new(i)(i=0,1,.......,29)},对其中的s_new(9),s_new(18),s_new(27)进行改进处理,得到对应的值s9、s18、s27;
(2)将s9、s18、s27分别量化到[0,255]区间,量化公式如下:

式中q1、q2、q3分别为量化后的值,[_]表示8bit截断操作。
(3)对图像中的第1个像素f(0,0),对q1、q2、q3和像素做如下操作:

用式(10)对f(0,0)进行扰乱得到新的像素值f′(0,0),过程如下:
![]()
(4)对其余的像素重复以上步骤,直到整幅图像完成像素值扰乱,得到图像f′(x,y);
(5)分别对f′(x,y)像素坐标按式(11)进行二维Arnold置乱。
定义:设有单位正方形上的点(x,y),将点(x,y)变到另一点(x′,y′)的变换为:
![]()
此变换称作二维Arnold变换。
考虑到数字图像的要求,Arnold变换可改写为:
![]()
其中N是数字图像的阶数,(x,y)为图像上像素点的坐标。将二维Arnold变换应用在图像f(x,y)上,可以通过像素坐标的改变而改变原始图像灰度值的布局。
(6)整个加密过程结束,解密是加密的逆过程。
四、实验结果及安全性分析
1、加密和解密实验结果
用一幅256×256大小图像在PC机上进行加密和解密实验。实验参数选择:系统尺寸L=30;用户密钥key1=0x34,key2=0xfe,key3=0xc4;Logistic映射参数μ=4;TCML系统耦合系数ζ=0.234;Arnold置乱轮数m=20。实验效果见图2。

2、安全性分析
(1)密钥空间分析
一个好的加密方案应该使其密钥空间足够大从而使得强行攻击不可行。在加密算法中,可扩展的外部密钥提供了所需安全等级的任意长度密钥,因此本方案密钥空间是足够大的。
(2)密钥敏感性分析
密钥敏感性,即密钥的微小差别可以对密文造成很大的变化,从密文中也就很难得出有关密钥的信息,从而获取密钥。在加密系统中,使用错误密钥的解密结果见图3。可以看出错误密钥对加密图进行解密无法得到原始图像的任何信息。

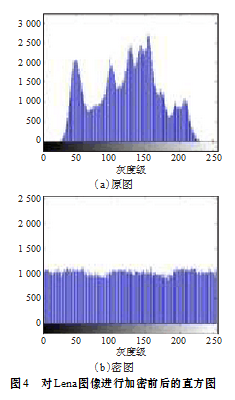
(3)直方图分析
图4为对图像进行加密前后的直方图。图4(a)和图4(b)比较,可见使用本算法所得的密图的直方图分布很均匀,完全掩盖了变换前的分布规律,才能使破译难度进一步增加。
(4)相邻像素的相关性
加密前图像中相邻像素的相关性明显很大,降低相邻两个像素的相关性才能破坏统计攻击。所以在原始图像和加密图像中各随机选1000对像素对,测试其相关性(垂直方向、水平方向),并进行相关系数计算。其中x,y表示像素灰度(两个相邻)。在测试中,使用如下3个离散化公式:
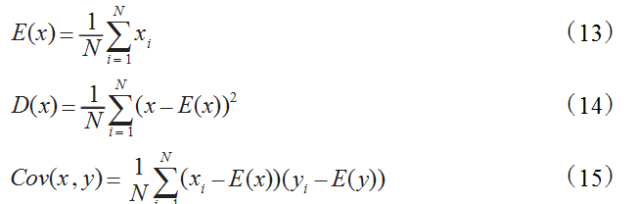
图5给出了利用本算法对Lena图像进行加密前后图像的相邻像素水平相关性。
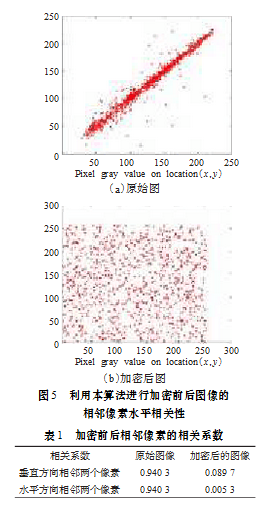
表1列出了图像加密前后相关系数(水平,垂直方向)。由表1和图5可见,加密后图像相邻像素间的相关性要远小于Lena原图像的,这表明本算法具有较强的抗统计分析能力。
(5)差分攻击
攻击者通过图像中很小的一点(例如一个像素)来观察加密后图像的变化,来破解加密图像。
这里以原始图像一个像素的改变对加密图像的影响为例测试了差分攻击。先定义了两个量:归一化平均变化强度(UACI)和像素变化率(NPCR)。令加密图像(两幅)分别为C1和C2,这些图像只有一个像素的改变。像素在位置(i,j)的灰度值为C1(i,j)和C2(i,j)。定义一个二值矩阵D,它和C1与C2有相同的尺寸。若C1(i,j)=C2(i,j),则D(i,j)=1;否则D(i,j)=0。
NPCR定义为:
![]()
UACI定义为:
![]()
经过计算可以得到NPCR=0.424%,UACI=27.12%,由此可见算法不仅仅对密钥是敏感的,对要加密的图像也是非常敏感的,可见可以有效地抵抗差分攻击。
小知识之耦合
耦合是指两个或两个以上的电路元件或电网络的输入与输出之间存在紧密配合与相互影响,并通过相互作用从一侧向另一侧传输能量的现象;概括的说耦合就是指两个或两个以上的实体相互依赖于对方的一个量度。











