针对以往光学图像加密系统中输入面和频谱面对称性的缺点,在不增加系统元件的基础上,利用球面波照射不对称非标准傅里叶变换系统进行图像加密。通过把相位掩模置于该系统的傅里叶变换平面,利用不对称非标准傅里叶变换系统的输入面和频谱面的不对称性以及频谱面对于点光源相关参数的依赖性,克服了以前光学加密系统中输入面和频谱面的对称性所带来的安全隐患,并且获得了除相位掩模以外的另外四重密匙。
一、基于不对称非标准傅里叶变换的光学图像加密基本原理
基于不对称非标准傅里叶变换加密系统原理设计的加密系统如图1所示。
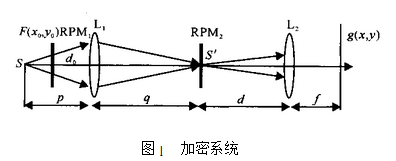
图1左半部分是一个点光源照射的傅里叶变换系统。其中,s和s'互为像共轭关系,即1/p十1/q=1/f。该系统的频谱面位于s'所处的平面上,其位置不是固定的,随透镜的焦距f和点光源与透镜的距离p的变化而变化。如果把相位掩模置于该系统的频谱面上,则相位掩模的纵向位置以及透镜的焦距也将成为密匙 。图1右半部分是1个非标准傅里叶变换系统,它的输出面位于第2透镜的后焦面上,输入面(S'所处平面)与第2个透镜的距离d可以自由变化,这样d也可作为密匙控制相位掩模的位置 设整个系统输入面(S所处平面)的坐标为(xo,yo),S'所处平面的坐标为(ξ,η),输出面的坐标为(x,y)。RPM1和RPM2分别为独立的随机相位函数exp[jb( x0,y0)]和exp[jb(_ξ,η)]。系统加密时,待加密图像f(zo,yo)与exp[jn (x0,yo)]相乘完成空域编码,然后经第1个透镜L1。作傅里叶变换,可得傅里叶频谱面上的光场分布:

式中:![]() U(ξ,η)与第2块相位掩模exp[jb(_ξ,η)]相乘完成频域编码,再经过第2个透镜L做傅里叶变换,最后可得输出平面上的光场分布:
U(ξ,η)与第2块相位掩模exp[jb(_ξ,η)]相乘完成频域编码,再经过第2个透镜L做傅里叶变换,最后可得输出平面上的光场分布:
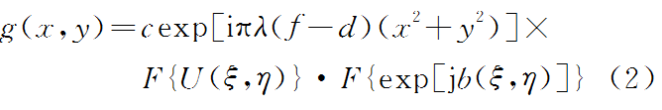
式中:![]() 显然(2)式是一个随机白噪声,可作为最后的加密图像。
显然(2)式是一个随机白噪声,可作为最后的加密图像。
解密时,(2)式不是U(ξ,η)与exp[jb(_ξ,η)]乘积的严格傅里叶变换,存在着相位弯曲,所以对(2)式进行标准的逆傅里叶变换就不可能得到U(ξ,η)与exp[jb(_ξ,η)]的乘积。根据光路的可逆性,我们可得到U(ξ,η)与exp[jb(_ξ,η)]乘积的共轭。只要把g(x,y)*置于图1的右端输入,就可在距离透镜d处,S'所处的平面上得到U(ξ,η)与exp[jb(_ξ,η)]乘积的共轭,然后与exp[jb(_ξ,η)]相乘进行频域解码。同理,可以在原加密系统的输入面上得到f(xo,yo)与exp[jn (xo,yo)]乘积的共轭。如果f(xo ,yo)是正的实函数,则可用CCD接收解密图像。
二、安全性能分析
从上面的图像加密、解密过程可以看出,采用不对称非标准傅里叶变换系统进行傅里叶变换时,傅里叶变换式前有一个相位因子,使光场产生了相位弯曲,因此解密时,系统不可能像4f系统那样进行2次简单的逆傅里叶变换.必须利用加密图像的共轭g(x,y)*从原加密系统的输出端输入,在原加密系统的输入端接收解密图像。系统的有关参数do,d,p(或q)和f在解密时必须己知,否则就解不出原图像。具体分析如下:
根据菲涅耳衍射原理可知.如果解密相位掩模位置与透镜L2:的距离不等于d,则得不到U(ξ,η)与exp[jb(ξ,η)]乘积的共轭。同理,如果解密时do和q的大小与加密时不一致,将不能恢复原图像,另外,从(2)式可知,要想用1个对称的标准傅里叶变换系统获得U(ξ,η)与exp[jb(_ξ,η)]的乘积,就必须设法抵消相位因子exp[i兀λ(f -d)(x2+y2)]。由于透镜的透过率函数exp[±πi(x2+y2)/λf与该相位因子具有相同的形式,因此比较2式可知,若用1个透镜抵消此相位弯曲,那么这个透镜的焦距必须与1/λ2(f'-d)相等;如果f和d未知,则不能抵消这个弯曲。因此,只能利用光路的可逆性解密和加密图像,由以上分析可知!采用该系统进行图像加密比4f系统多出几重钥匙!大大提高了系统的安全性能。
三、计算机模拟与分析
为了验证该方法的可行性,我们利用灰度图像进行计算机仿真实验,并验证在己知解密相位掩模而不知系统相关参数的情况下不可能解密出原图像。仿真时,采用波长为600 nm的发散球面波来照射不对称非标准傅里叶变换系统.取球面波的半径p为30 cm(或q为60 cm),透镜焦距f为20 cm,do为10 cm,d为15 cm,图像的像素为25 6×2 5 6。 图2是对灰度图像进行加密和解密所得的仿真结果。图3是在己知解密相位掩模而不知系统相关参数的情况下,对灰度图像进行盲解密所得到的图像。


从上述理论分析和模拟实验可以看出,在4f系统不增加系统元件,利用球面渡照射不对称非标准傅里叶变换系统进行图像文件加密是完全可行的。由于采用不对称非标准傅里叶变换系统进行图像加密和解密,所以系统中每个透镜的输入面和输出面不象4f系统和分数傅里叶变换系统那样与透镜对称,并且系统的参数可以变化,因此,利用该系统加、解密时,除了与4f系统具有相同加密效果外,还成功地克服了4f系统中相位掩模的纵向位置不能作为密匙的缺点,系统具有不对称性。这些特点大大增强了系统的安全性能。
小知识之傅里叶变换
傅里叶变换能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。在不同的研究领域,傅里叶变换具有多种不同的变体形式,如连续傅里叶变换和离散傅里叶变换。最初傅里叶分析是作为热过程的解析分析的工具被提出的。











