随着信息技术的发展,越来越多的图片通过互联网、无线通信等渠道传播。如何保护图片的安全,防止非法攻击,成为一个日益严重的问题。传统加密算法DES、IDEA、RSA等得到了成功应用,但这些加密算法是根据文本文件加密的特点提出来的,在加密图像时,由于图像具有信息量大、相邻像素值相关性强等特点,因此不能完全满足图像加密需要。为此我们今天给大家介绍一种基于图像分割思想的二维混沌映射图像加密算法。
一、新二维混沌映射原理和算法
1、新二维混沌映射原理
设图像大小为N×N。首先沿图像的对角线方向,将方图分割为上下两个等腰三角形图像。由于等腰三角形图像每一列的像素数目和相邻列的像素数目是不同的,因此可以从水平方向,将一列中的像素插入到相邻列的像素之间。反复该过程,依次连接,原始图像被拉伸成为一条长N2的直线。然后,再折叠成一个N×N的新图像。如图1所示,(a)为左映射,(b)为右映射。
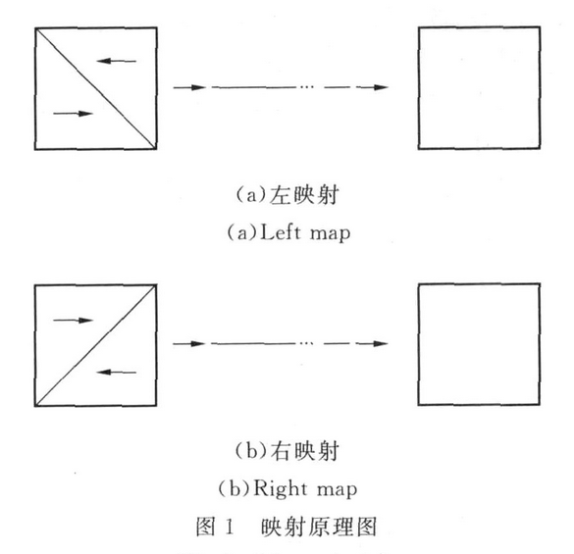
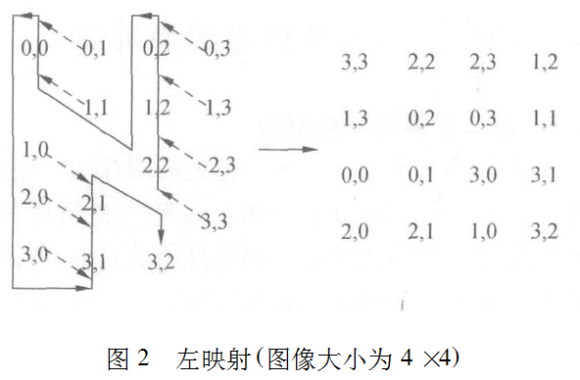
举例说明:设图像大小为4×4,如图2所示,当映射为左映射时,则首先将图像沿左上到右下的对角线方向分割为两个等腰三角形图像,依次将像素(3,3)插入到像素(2,2)之前,像素(2,3)插入到像素(2,2)和(1,2)之间,像素(1,3)插入到像素(1,2)和(0,2)之间……重复这个过程,即可将原图像拉伸成为一条直线:(3,3)、(2,2)、(2,3)、(1,2)、(1,3)、(0,2)……最后将直线折叠,得到映射后的新图像。
当映射为右映射时,首先将图像沿右上到左下的方向分割为两个等腰三角形图像。像素插入方向和左映射时相反。上述插入过程均采用将较长的列像素插入到较短的列像素之间的方法,避免了当列的个数为奇数时,出现一列像素无法完成插入操作的问题。
2、新二维混沌映射计算算法
图像大小为N×N,设A(i,j),i,j=0,1,…,N-1为图像中的任意一点像素值,l(i),i=0,1,…,N2-1,为将A(i,j)拉伸后的一维向量。由于映射是由左映射和右映射两个子映射组成,分别给出算法如下:
左映射算法。如图1(a)所示,左映射算法为:当j≥i且N-j是奇数时,有:
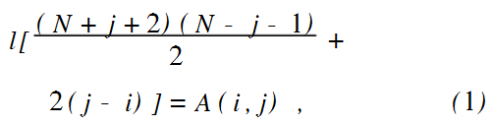
当j≥i且N-j是偶数时,有:
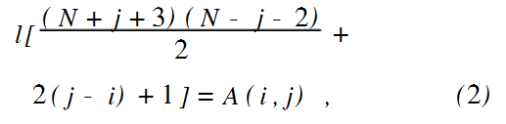
当j<;i且j是偶数时,有:
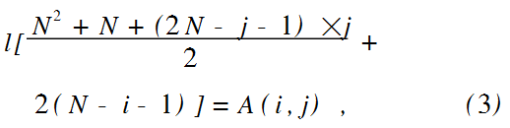
当j<;i且j是奇数时,有:
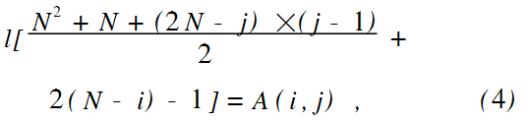
右映射算法。可以通过下列过程得到:将原图做一次镜像,A′表示映射后的图像:
![]()
其中,i=0,1,…,N-1;j=0,1,…,N-1。通过左映射算法(1)~(4),得到右映射算法——折叠算法。
![]()
其中,i=0,1,…,N-1;j=0,1,…,N-1。
二、图像加密、解密算法
映射分为左映射和右映射,其映射次数可以作为密钥Key。如Key=1234,表示依次用左映射1次,用右映射2次,然后用左映射3次,最后用右映射4次。由于图像是有限像素点的集合,像素的排列组合是有限的。因此在有限次迭代之后,加密图像会恢复到原来的状态,即混沌映射都具有庞加莱回复性。Fridrich[10]指出,当迭代次数较小(如<;15)时,加密算法是安全的。本文将密钥的每一位设计为小于10的整数。由于新混沌映射的周期非常大(不小于105),这种设计是合理的。
加密算法如图3所示。
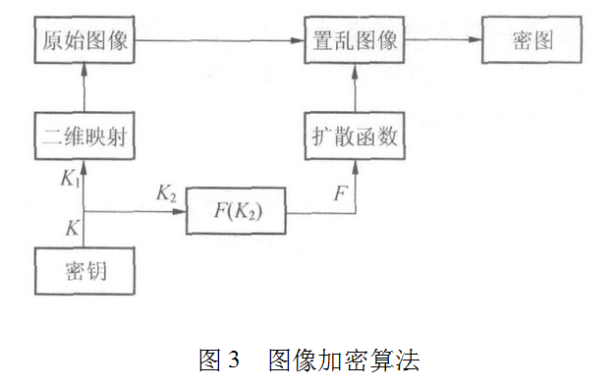
其中K1及K2可以分别是密钥K的一部分,也可以相同,或可互相推导,函数F(K)为密钥的函数,输出为扩散函数的参数。
本文采用了一种简单的扩散函数:
![]()
其中,vk是指每一个像素的值,vk′为扩散后的像素值,v-1′=F(K2),G(vk-1′)=5×vk-1′,L为像素灰度级。该扩散函数结构简单、扩散速度快。
图像加密算法分为三步:
(1)利用密钥K1及算法(1)~(5),将图像A(i,j)拉伸处理为一条直线l(i),其中i=0,1,…,N2-1。
(2)利用算法(6),将直线折叠处理,得到置乱图像B(i,j)。
(3)利用密钥K2及扩散函数,对置乱图像进行扩散处理得到密图。
解密算法与加密算法密钥相同、过程相反。
由于密钥相同,该加密算法为对称加密算法。
三、加密实例和安全性能分析
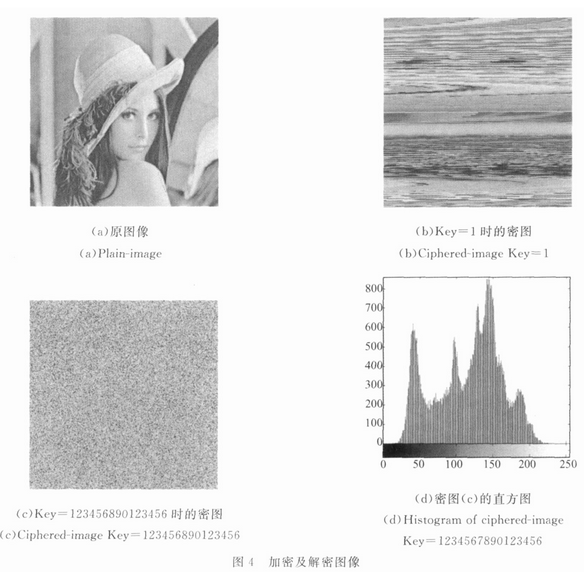
对L=256的lena图进行加密。为了研究二维混沌映射的加密效果,首先令K2=0,即不使用扩散函数。此时,加密系统仅仅置乱图像,没有改变图像的像素值。当Key=1时,使用该映射加密之后,图像没有原图的特征,如图4(b)所示。而Bakermap在加密次数为1时,图像特征明显。如图4(c)所示,当Key=1234567890123456时,密图用肉眼已无法识别,说明加密效果良好。密图直方图如图4(d)所示。
1、安全分析
密钥空间
由于最基本、最流行的破解方法是对密钥进行穷尽搜索,密钥空间大是加密算法安全的前提。加密算法的密钥空间(无扩散函数)如表1所示。
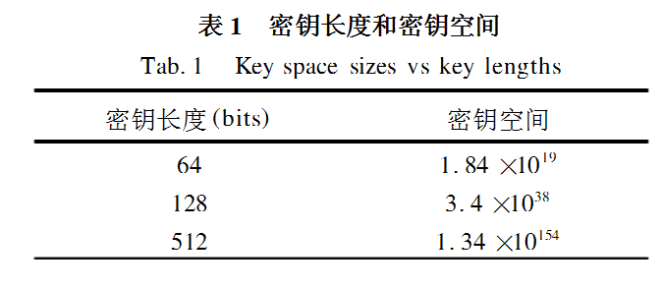
研究表明,密钥空间大小只和密钥长度有关,在理想情况下(计算速度允许),密钥能无限增加。
密钥敏感度
对用Key=1234567890123456加密的密图,用Key1=1234567890123455解密,如图5(a)所示。用Key2=1234567890123457解密,如图5(b)所示。可以看到,即使加密密钥和解密密钥仅有很小的差异(1位),也无法解密密图,证明加密算法对密钥非常敏感。

统计分析
于图像相邻像素之间具有很强的相关性,因此,如果加密后相邻像素之间相关性越趋近于零,越能说明加密算法的安全性。相邻的相关系数如下:
![]()
其中x、y为两个相邻点的灰度值,
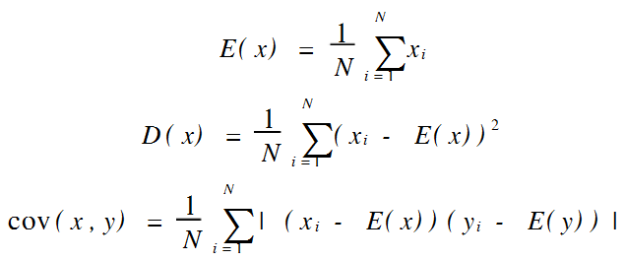
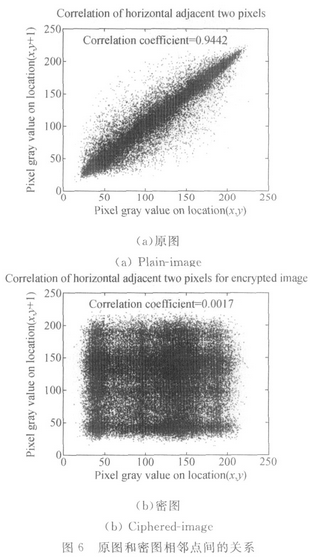
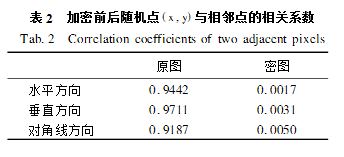
图6为密图像素(x,y)和(x,y+1)之间的关系。原图的相关系数为0.9442,加密之后的相关系数为0.0017。其他相邻点的相关系数如表2所示,可见加密后密图像素之间的相关系数非常小。
2、扩散机制
仅对图像进行像素置乱不够安全,不能抵御已知(选择)明文攻击。因此,为了增强加密算法的安全性,需要在二维混沌映射的基础上增加扩散函数。本文采用的扩散函数如式(7)所示,其中令v-1=F(K2)=150,增加扩散机制之后,原图的像素值发生改变。加密后的图像和直方图如图7所示:
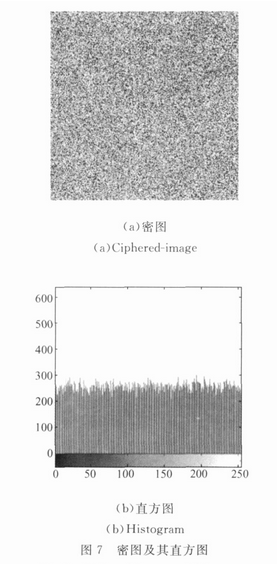
在增加了扩散函数之后,为了检验加密算法扩散性,对两个只有一个像素点有差异的图像进行NPCR(NumberofPixelsChangeRate)和UACI(UnifiedAverageChangingIntensity)分析。两图像的像素值分别为v1′和v2′,如果v1′(i,j)≠v2′(i,j),则D(i,j)=1
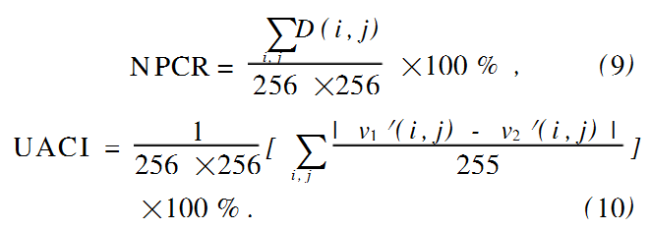
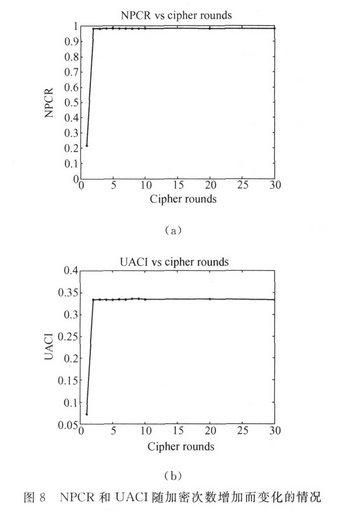
结果表明,在参数不变的情况下,即使只是两个有一位像素不同的图像,随着加密次数的增加,密图也会变得完全不同,扩散速度非常快。如图8(a)所示,当加密次数n=2时,两个加密图像便已基本不同(NPCR≈1)。
四、新映射与其他混沌映射比较
Bakermap是最典型、应用最广的混沌映射之一,在图像加密领域得到广泛的应用。新映射和Bakermap比较:
(1)密钥空间更大
介绍了Bakermap的两种形式,但即使是Bakermap的一般形式(即密钥不是图像大小的因数的情况),Bakermap的密钥空间最大仅为2N-1(N为图像的宽),而新映射的密钥空间只和密钥本身长度有关。只要计算速度允许,密钥长度没有限制。
(2)对密钥变化更加敏感
新映射只要密钥稍有变化,密图就会截然不同。因此,用相似但不相同的密钥无法对密图解密。而使用相似的密钥也可以对Bakermap加密密图进行解密。
(3)加密算法更加简单
Bakermap一般形式下的算法具有非常复杂的形式。加密算法比较复杂。而新映射算法简单,加密算法非常简洁。
(4)能满足实时加密需要
在一台PentiumIII(M)1.13GHz的笔记本电脑上仿真结果表明,未优化的VC程序,Key=1234567890123456时,加密速度约为3Mb/s。
本文根据折叠、拉伸的思想,得到一种新的二维混沌映射,提出一种新的图像加密算法。仿真结果表明:图像加密算法密钥为64bit时,密钥空间为1.84×1019,加密速度约为3Mb/s,基本满足实时图像加密需要。使用新映射的优点是:
(1)算法非常简单,容易编程实现。
(2)二维混沌映射是可逆的。
(3)基于二维混沌映射的加密/解密算法没有信息损失。
(4)具有与其它混沌映射一样的性质,能应用于信息安全的其他领域。
(5)加密的密钥基本没有限制,在速度允许的前提下,可以为任意整数(每位最好<10)。
(6)密图和原图大小一致,没有大小差异。
(7)能满足实时需要,适合大尺寸图像加密。
(8)加密算法简单,容易硬件实现。
由于压缩后的图像也可以表示为二维矩阵形式,因此,混沌映射加密算法如何结合流行的图像压缩技术,对压缩后的图像进行加密,将是一个值得探讨的问题。
小知识之图像分割
图像分割就是把图像分成若干个特定的、具有独特性质的区域并提出感兴趣目标的技术和过程。它是由图像处理到图像分析的关键步骤。现有的图像分割方法主要分以下几类:基于阈值的分割方法、基于区域的分割方法、基于边缘的分割方法以及基于特定理论的分割方法等。











