适用于数据库的加密算法 - 夏冰加密软件技术博客

数据库加密方法可以应用于不同的环境，但存在一个共同的问题是：对于所形成的密文数据库无法进行操作。这样首先增大了时空开销；其次，在实际应用中，对于某些重要或敏感数据，无法满足用户对其进行操作但又不让用户了解其中的信息的需要。如果能对密文数据库进行数学运算和常规的数据库操作，显然能够解决上面存在的问题，并可以大大削减加、解密所需要的时空开销，大大提高数据库的运行效率。秘密同态技术就是一个能解决上述问题的有效方法。

一、秘密同态技术在整数上的实现

秘密同态是由Rivest等人于1978年提出的，是允许直接对密文进行操作的加密变换。但是由于其对已知明文攻击是不安全的，后来由Domingo做了进一步的改进．秘密同态技术最早是用于对统计数据进行加密的，由算法的同态性，保证了用户可以对敏感数据进行操作但又不泄露数据信息．秘密同态技术是建立在代数理论之上的，其基本思想如下：

假设Ek1、Dk2分别代表加密、解密函数，明文数据空间中的元素是有限集合｛M1，M2，…，Mn｝，a和β代表运算，若a （Ek1（M1），Ek1（M2），…，Ek1（Mn）=Ek1（β（M1，M2，…，Mn））成立，且Dk2（a（Ek1（m1）、Ek1（M2），…，Ek1（Mn）））=β（M1，M2，…，Mn）成立，则称函数族（Ek1，Dk2，a，β）为一个秘密同态。

加密算法实现过程如下：

（1）选取安全大素数p、q，及由此计算m=pq（m保密）；

（2）选取安全参数n（根据需要选择适当大小）：

（3）明文空间T=Zm（小于Z的所有非负整数集合），密文空间T=（Zp*Zq）n；

（4）选取两素数rp、 rq，分别满足rp∈Zp，rq ∈zq;

（5）确定加密密钥为K=（p，q，rp，rq）；

（6）加密算法：

设有一明文x∈zm，随机地将x分为n分：X1，X2，…，Xn，并满足Xi∈Zm, i=（l,2,…,n）;_

（7）解密算法Dk （x）：

第一步计算

其中，rp-n和rq-n分别为rp mod p和rq rnod q相应次幂的乘法逆元。

第二步计算

第三步利用中国剩余定理计算

其中qq-1=1mod p，pp-1=1 modq。

二、浮点型数据同态加密运算

本文基于秘密同态加密的基本原理，在同态加密机制中提出了复合同态的概念并应用到浮点数的加密算法中，实现了浮点数的秘密同态加密，使得同态加密机制更具有通用性。

（一）复合同态的定义

定义设σ、τ分别是空间G到H和H到M的同态变换，则σ、τ复合σ*τ是空间G到l的同态变换。即对于x∈G，有同态变换y=σ（x）,（y∈H），存在z∈M，Z=τ（y）=τ（σ（x））=σ*τ（x）

满足：

基于实际的应用和讨论的方便，假设两次同态变换分别是加密运算Ek1（x）和Ek2 （y），由于引入复合变换的目的是将浮点数转换成整数的形式然后进行加密，所以定义Ek1（x）是对浮点数进行的加密运算。Ek2 （y）仍然采用整数上秘密同态变换的加密机制。

（二）浮点数到整敛的同态加密变换

加密算法的实现过程如下：

（1）设明文数据x的小数点位数为k （k为非负整数）；

（2）将原数据分解为xo，x1，…xk，使得x*10=ko*10o+x1* 101+...+Xk*10k，其中x1为正整数；

（3）定义同态加密变换

（4）则解密运算为浮点数。

在浮点数的加、减、乘、除运算中，根据实际的需要设定所有明文数据的最大小数点位数为k（k为非负整数），不够k位的用零补足，则有：加和减Ek1（x±y）=E k1（x）±E k1（y）为10的i（0≤i≤k）次方项的加减法。

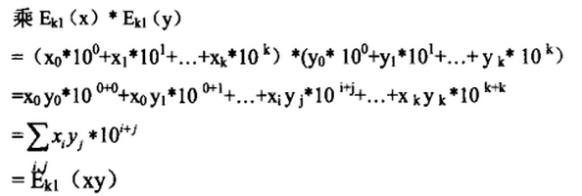
适用于数据库的加密算法

其中o≤i≤k，o≤j≤k， o≤j+j≤2k。

除因为Ek1（x）只是一数值形式的变换，显然有，由上述加减乘除运算可得：

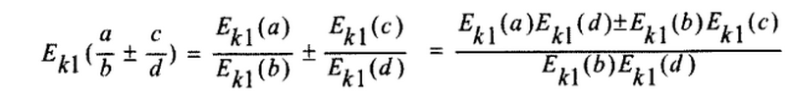
适用于数据库的加密算法
这些运算保证了可以直接对转换后的整数进行操作。

将浮点数进行复合同态加密，即将浮点数明文x经过Ek1（x）同态变换后，转换成一整数的形式，然后再用Ek2 （y）（其中y=Ek1（X））进行加密变换。

其中解密运算定义为Dk（X）=Dk1（Dk2 （x）），Dk1，Dk2分别为Ek1和Ek2的解密运算。解密过程中首先对Ek1（x）形成的密文数据进行解密，然后再利用Dk1（x）计算得到明文数据。

（三）复合同态基本运算

复合同态运算完成的是浮点数的同态加密过程，也是本部分的核心。

下面的基本运算包括上面讲述的浮点数到整数的同态转换E k1（X）以及整数上的同态加密算法E k2（X），具体实现过程如下：

1．复合同态的加、减法运算

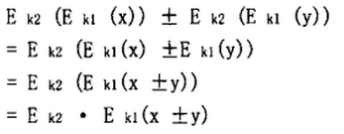
适用于数据库的加密算法

2、复合同态乘法运算

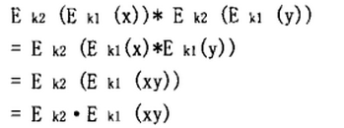
适用于数据库的加密算法

3、复合同态除法运算

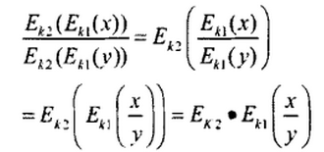
适用于数据库的加密算法

即对经过复合同态加密后得到的密文之间的加、减、乘、除运算就相当于对明文进行基本运算后再加密。

（四）安全性分析

将同态加密机制的应用从整数扩展到浮点数范围内，使秘密同态加密算法更具有实用性。加密过程中即使经过Ek1（x）加密转换后得到相同的数据，由于第二次同态加密素数的随机选取和加密数据的随机分割，这样得到的加密数据也是不一样的。浮点数同态加密即在外层加密中保留了原始秘密同态加密的安全性，同时也对原数据进行了双重同态变换，在安全性上只有过之而无不及。在浮点数上的同态加密机制在安全性方面同样有以下特性：

（1）仅知密文攻击：如果攻击者获取密文，但从n找出p是非常困难的，因为需要对n进行因数分解。

（2）已知明文攻击：如果攻击者获取一个明文密文对（x，y），攻击者可以进行反复的试探，以期获得解密密钥p；但攻击者需要进行试探运算的运算量大到不可以接受的地步。

（3）完整性攻击：根据我们的加密算法，攻击者可以任选一个值来替换一个已经加密的数据。也就是说，我们的算法无法抵抗完整性攻击。

三、字符串数据的同态加密

与整数不同的是，整数加密后能够实现的在密态下的加、减、乘、除运算对于字符串是没有意义的，所以本文通过中国剩余定理将字符串进行转换，然后利用秘密同态算法进行加密处理。具体算法如下：

（1）设一字符串B，将字符串中的每一个字符取其ASCII码，分别表示为b1，b2，....，bk，其中k是字符串中字符的个数。

（2）对应取k个两两互素的正整数，设为m1，m2，...mk，（m1≥121）。

（3）则由中国剩余定理得同余式组。

（4）则同余式组的解就是将要加密的整数值。