前面我们已将介绍了两种电子商务中的混沌加密算法,下面我们就来说一下第三种:混沌对称分组加密算法。
混沌对称分组加密算法
1、基于混沌置换网络的分组密码
用Logistic映射产生置换网络,置换网络是输入集A到输出C上的双射变换:fk;Ak→C,式中k为控制输入的变量,密码学中则为密钥。这里A是输入的n个明文量,C是n个输出的密文量,K为密钥矢量。双射变换要求在给定的k下可以从密文中唯一地恢复出明文,本文利用混沌序列来实现置换网络的坐标变换,即将明文向量A= (a0,a1,…,an-1)的各个分量进行置换,得到密文向量C= (C0,C1,…,Cn-1),其置换坐标由混沌序列在给定初始值下迭代产生的序列{xo,x1,…,xn-1l}来得到,这里xo即为密钥.其中:标志数组Flag[k]为遍历标志,当Flag[k]=FALSE时,表示(k/n,(k+1)/n)区间未遍历到。i为已遍历区间的个数j为Logistlc映射已经迭代的次数,为了使由于初值取得不好时置换过程能够结束,这里当迭代次数j>30n时,重新选取初值.实际应用中要考虑有限精度对混沌序列的影响,使序列不脱离混沌态,一般混沌序列的精度应大于32位。
然而,已有文件基于混沌置换的分组加密的安全性,并给出了相应的攻击算法。混沌序列的截尾序列的相邻值之间具有很强的相互制约性,且前若干值主要由初值的高位比特决定,一个安全的分组加密算法不仅要有足够的分组规模,而且还必须满足混乱和扩散标准,所设计的算法必须能经得住选择明文等攻击方法的考验,在将混沌变换应用于密码领域时,必须设法克服混沌变换的自身弱点。
2、 8位分组的反馈型混沌分组密码
在该分组加密算法中,混沌映射的系统参数和初始条件依赖于外部输入的可变长度密钥,通过应用反馈技术增强抵抗各种攻击的能力,每一分组明文的加密都依赖于前一分组明文的加密,加密算法描述如下:
①首先将明文/密文分成8位一组,例如,明文/密文的每一个符号就是一个单独的分组,n个分组的明文和密文可以表示为:
![]()
用128位密钥直接进行加密/解密不太方便,因此它被分割成8位一组的分段密钥。
![]()
②加/解密过程使用Logistic映射,xn+1=μxn(1-xn),x∈(0,1],μ∈[3.57,4.0]。
应用下列等式产生一个实数Xs,Xs∈(0,1)和一个伪随机数Ns。
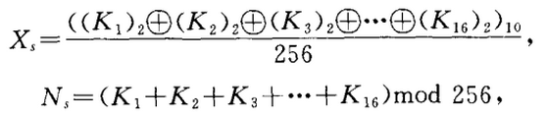
其中,Kn,(Kn)2,(.)10和+分别代表第n个分段密钥的ASCII码值、第n个分段密钥ASCII码值的对应二进制值、二进制对应的十进制值和异或操作。
③随机选择一个分段密钥(Kr,1≤r≤16)并修改作为初始条件的种子密钥(Xs)和迭代次数Ns:
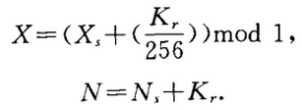
X和N分别作为Logistic映射的初始条件和迭代次数。
④通过应用下述修正线性匹配随机数发生器(mLCG)得到系统参数值。
![]()
其中a是乘法因子,m和c是常数,μi是第i个分组明/密文块加/解密时的系统参数值,当i=1时,Yi=0,当i=2,…,n时,yi由下列标准LCG发生器计算得到:
![]()
选a=16,c=7,m=81。
⑤Logistic映射的迭代值Xn+1,通过下述等式被用于加/解密明/密文。
![]()
对下一个分组明/密文块,用Xn+1,和Ci-1,作为下一次迭代的Xs和Ns,通过这种方式,引入反馈机制使加密系统更加强健。
小知识之置换
将顶点的变换用矩阵的形式表示的一一对应叫做置换。











