电子商务中的混沌加密算法—混沌序列加密算法

现今电子商务中使用的加密方法可分为4种：序列加密算法、对称分组加密算法、单向散列函数和公钥分组加密算法。那么，接下来我就给大家详细的介绍一下第一种加密算法—混沌序列加密算法。

混沌序列加密算法

混沌信号具有天然的随机性，特别是经过一定处理后的混沌信号具有非常大的周期和优良的随机性，完全可以用来产生符合安全性要求的序列密码。初始状态只有微小差别的两个同构混沌系统在较短的时间后就会产生两组完全不同的、互不相关的混沌序列值，因而能提供数量众多的密钥或密码流。经过合理设计的混沌序列密码加密算法不会随着对符合要求的密钥流数量的提高而复杂化，混沌序列是一种非线性序列，其结构复杂，难于分析和预测，可以提供具有良好随机性、相关性和复杂性的拟随机序列，这些很有吸引力的特性，使其有可能成为一种可实际被选用的序列加密体制。

1、基于m序列扰动的混沌序列加密

一种随机改变混沌映射参数来提高混沌序列复杂性的方法如图1所示，这种方法在有限精度实现时，使得输出序列的周期增大并可以度量。同时，为了进一步提高输出混沌序列的随机统计特性，对输出混沌序列引入了m序列的随机扰动。

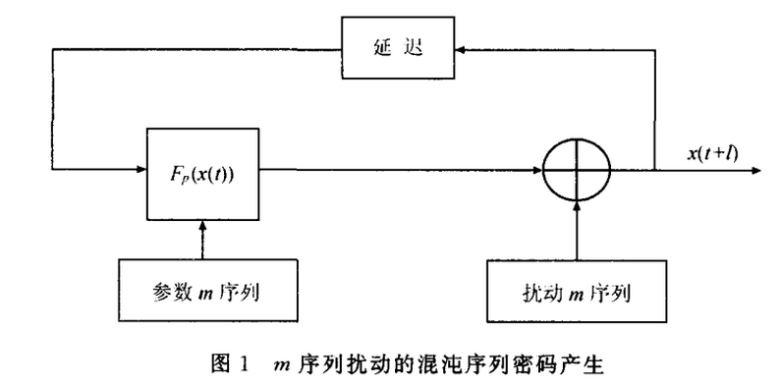
电子商务中混沌加密算法

其中：Fp(x(t))为一维分段线性映射，其定义如下：

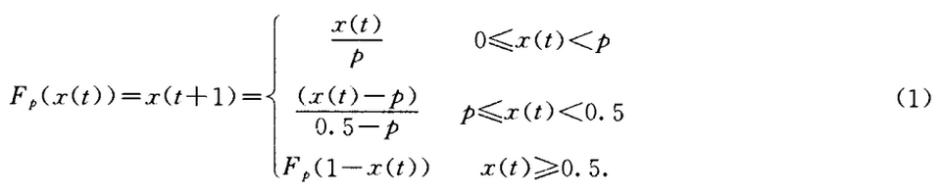
电子商务中混沌加密算法

为了软件和硬件实现方便，用np级m序列的2np-1个状态作参数周期性变化的混沌系统的2nP -1个混沌映射的参数，图中肌序列在迭代过程中，每迭代一次就改变一个状态，为了使m序列的状态值满足混沌参数O<p<1/2的要求，令m序列的状态(C1，C2，…，Cnp)与混沌参数户的对应关系如下：

显然，P在[2-(np+1)，1/2-2-(np+1)]之间以2-(np+1)为间隔均匀分布，共有2np -1个不同的值，为了进一步改善混沌系统输出序列的随机统计特性，在其输出上引入一个优序列的随机扰动，扰动幅度。设扰动m序列的级数为ns，扰动幅度由该序列连续nr位决定，扰动幅度和一维迭代相图上的最大斜率km的关系为：nr≥log2(km+1)。

为了生成混沌序列密码，必须将混沌序列信号{x(t)}转换成二进制的0-1序列流{Sn(t)}，为此引入不可逆转换函数Tn(x(t))。转换函数Tn(x(t))定义如下：

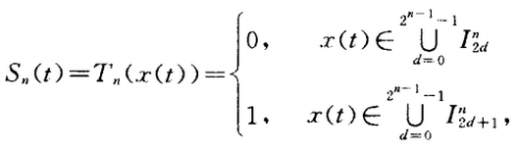
电子商务中混沌加密算法

其中n>0为任意正整数，I0n，I1n，I2n，…是[O，1]区间的2n个连续的等分区间。由于混沌序列信号{x(t))具有良好的随机统计特性，这样生成的{Sn(t)}在理论上具有均衡的0-1比和δ-like的自相关等优良的统计特性。

有限精度实现时，混沌序列周期变大而且可以度量，由于混沌参数在每次运算前都发生了变化，即使对同样的x(t)，其输出x(t+1)也不相同，在有限精度运算下，如果参数周期性变化，即使迭代达到了已经出现过的状态，只要混沌参数与上次达到该状态时的不同，混沌也不会陷入循环，只有当达到该状态时，混沌参数也回复到原有值的条件下，混沌序列才可能进入循环，因此，混沌序列的周期一定是混沌参数变化周期的整数倍．由此可见，混沌参数周期性变化不但能提高混沌序列的复杂性，而且有限精度实现时，输出混沌序列的周期变大并可以度量。

2、基于混沌序列驱动的序列加密

利用混沌构造流密码可以采用如下几种方法：①用混沌序列代替传统的LFSR序列驱动非线性组合器；②用混沌迭代代替传统的非线性组合器；⑧同时应用前两者，而模型中的密钥Z则相应的变为混沌迭代的参数和初始值。

混沌序列驱动的序列密码以非线性组合密码为例，如图2所示，用混沌序列代替了传统的LFSR序列来驱动非线性的组合器，f为非线性组合函数，非线性组合函数通常采用如下的形式：

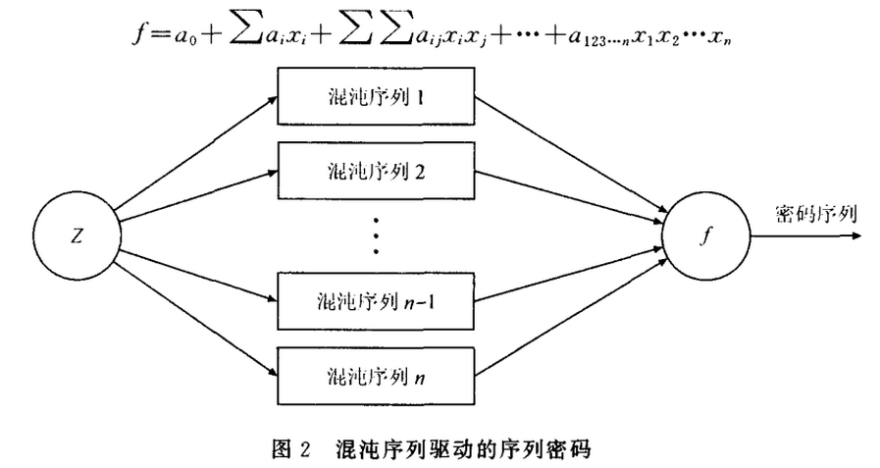
电子商务中混沌加密算法

混沌序列的获得可以采取如下的方法：采用Logistlc映射，Logistlc映射由下式给出：

该映射的轨道点密度为：

为保证迭代的当前序列值与前一个序列值独立，产生随机的序列，可以采用非线性量化的方法得到二进制序列，分点d满足如下的条件：

可以解得d的值为0，通过下列的方法可以得到二进制的序列：

在给定不同初值x0的情况下，通过迭代可以得到一系列的二进制的序列，将这些序列代替传统的LFSR序列，驱动非线性组合部分，可以实现混沌驱动的流密码体制，和传统的LFSR序列相比，混沌映射序列的周期长，复杂度高，同时由于混沌系统对初态的极端敏感性，想恢复出混沌序列，必须知道迭代的初值，不可能通过有限长的序列来预测整个序列，大大提高了密码的抗攻击性。通过改变迭代的初始值，可以得到大量的随机性能良好的混沌序列，解决了LFSR序列数量有限的问题。