基于被扰动的Lorenz系统的混沌加密算法
为了应对有限精度产生的混沌动力学特性退化问题,近年来有许多的改进方案,为此,我们提出一种基于被扰动的Lorenz系统的混沌加密算法。该加密算法能够在保证加密速度的前提下,使得混沌序列随机性、加密系统安全性等方面都优于基于三维混沌密码系统和基于联合混沌加密系统。
一、基于被扰动的Lorenz系统的混沌加密算法设计
1、对Lorenz系统参数的扰动
Lorenz系统是一经典的三维混沌系统,其动力学方程为:
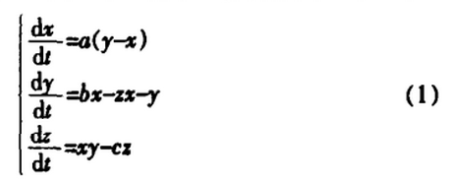
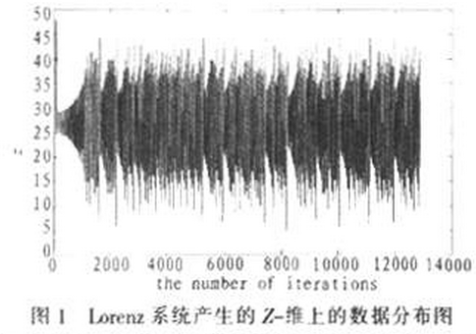
其中a、b、c是系统参数,该系统当a=1O、b>24.74、c=8/3时,系统进入混沌状态。然而在精度有限的计算机上模拟计算的过程中,当迭代次数较大时,z维上的数据会出现短周期的
现象,如图1所示。
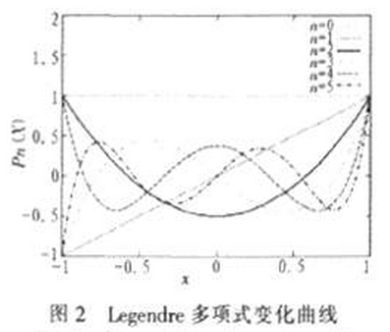
往介绍扰动过程之前先引入Legendre多项式:
Legendre方程:
![]()
式(2),当|x|<1时,可得到有界解,并且当n为非负整数,即n=0,1 ,2,3...时,在x=±1点亦有有界解。这种情况下,随n值变化方程的解相应变化(如图2)。
构成一组由正交多项式组成的多项式序列,即:Legendre多项式:
![]()
其递增表达式由(3)式给出:
![]()
Legendre多项式产生具有自相关性和较高的线性复杂度性的,均值伪随机序列,利用它来对混沌系统参数进行扰动。提高了混沌序列的随机性、复杂性。弥补了计算机等数字系统有限精度所带来的不足,从而增强加密系统的安全性。
选取b作为扰动的系统参数,具体扰动过程如下:
1)选定初始值x0∈(-1,1),利用式(3)。通过迭代,得到一个序列:
![]()
2)将序列bm应用到Lorenz系统的每一次迭代中,Lorenz系统在每一次迭代前,首先通过下面公式:
![]()
得到每一次迭代需要的b,从而扰动了Lorenz系统中的系统参数b。
2、算法描述
本法选用的混沌系统为Lorenz系统,首先利用Legendre多项式的递推式(3)产生序列bm,将这个序列值分别作为Loren系统(l)选代过程中系统参数b的改变值,Loren系统经过特定次数的迭代以后得到最后所需的混沌序列。这个特定次数(除第一次外)是由上一次加密的密文和当前的明文共同决定的,然后用混沌序列对原文信息进行加密操作。从而隐藏原文。
3、加密过程
本文以一副图像为例介绍具体加密过程。
似没.我们要加密一个图像文件P(N×M)。首先,将图像P(N×M)从定到右、由上而下进行扫描,将扫描到的数据放到P[N]中,具体加密方法如下:
1)将x0∈(-1,1)作为初始值代入(3)进行递推。递推50次得到序列:
![]()
2)对第m,(m+1)和(m+2)个像素加密时,将x,y,z,a=10,b=bm.c=8/3作为式(1)的初始值进行迭代,略去前500次迭代。以501次为起点继续迭代特定次数得到(特定次数是由待加密像前两个已加密的像索值决定)伪随机序列:
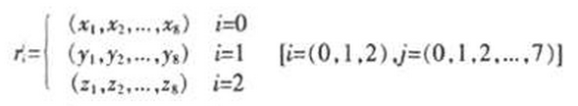
迭代过程中,每迭代一次,将b值按(4)进行变化,不断的对系统进行扰动。
迭代完成后,分别将第m,(m+1)和(m+2)个像素值p(m),p(m+1和P(m+2)与某一个rij进行异或操作得到密文c(m)和c(m+2)即:
![]()
其中,rij中i ,j的值由式(5)求的:
![]()
3)对图像文件前三个像素值文件加密时,首先用x,y,x,a=10,b=b1.c=8/3作为初值进行达代50次,由步骤2得到密文c(1).c(2)和c(3)。然后按步骤2依次对图像中的每个像素进行操作,最后将整个文件操作完毕,最后可以得到加密后的密文图像c。
4、解密过程
解密过程与加密过程相反,即:步骤2中提到的迭代的次数由前3个像素值决定。式(6)改为:
![]()
二、实验结果
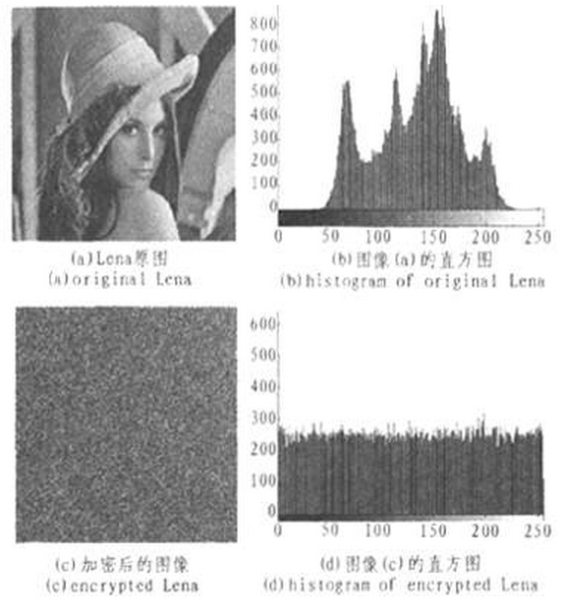
利用上述算法,Legendre多项式的初始值为x0=0.421518,Lorenz系统的初始值为x=1.184 07,y==1.362 86,z=1.25215和c=2.666 74。对256x256的lean图(图3(a))进行加密,图3(c)为加密后的结果。图3(b)和(d)分别是待加密图像和已加密图像的直方图。
小知识之扰动
一般是指系统在正常范围内的波动。它往往有一定的规律可循,并具有可预知性,为一般意义上的环境波动行为。











