目前,越来越多的信息需要通过网络来传蝓,这些信息不仅包括文本,而且还包括声音、数字固像和多媒体等,然而网络传输带宽十分有限,特别节约存储空间、加快传输效率,成为设计图倦加密方式实现要考虑的问置.传统的加密算法主要针对文本信息,而不针对图像文件,为此,我今天给大家介绍一种基于基于混沌序列的频域图像加密技术。
一、混沌系统
混沌现象是在非线性动力系统中出现的确定性的、类似随机的过程,这种过程既非周期又不收敛,并且对初始值有极其敏感的依赖性。通过混沌系统对初始值和结构参数的敏感依赖,可以提供数量众多、非相关、类随机而又确定可再生的信号。
由于上述特点,混沌已广泛应用干保密通讯中,同时也可以作为加密序列。混沌理论和数据保密的有机结合,是混沌理论研究不断深入和信息社会对信息安全的更高要求的必然结果。混沌加密技术已成为一种新兴的加密技术。
1、混沌的定义
设(X,p)是一致的度量空间。f:X→X是连续映射,如果f满足如下3个条件.称f在X上是混沌的。
(1)f具有对初值敏感依赖性;
_δ>0,使_x∈X及x的邻域N(x),_y∈N(x),当n≥O时,p(fn(x),fn(y))>δ
(2)f在X上拓扑传递;
_U,V开集,U,V _X,_k>0,使fk(u)∩v≠Φ
(3)f的周期点在X中稠密。
通常情况下,可采用Lyapunov指数、功率谱分析或Pioncare截面法来识别系统是否进入混沌状态。
2、 加密算法原理
图像文件加密系指将一幅明图经过某个加密算子的作用,变为可传输的密图,接收方将密图经过解密算子的作用,还原为明图;在传输过程中,即使密图被窃取,没有密钥很难或根本无法
完成解密。加密算法往往可以写成如下的变换式:
![]()
其中X明文X,密文Y和密钥k分别是有限长度的字符序列,他们的长度Lx,Ly,Lk可以不相等,方程(1)强调一个密文Y与一个明文X对应,函数由密钥的值来决定,既称为加密算法。
一般的数字图像包含大量的数据,但这些数据是高度相关的,对于静止图像往往含有大量的空间冗余信息。在该文提出的算法中,把混沌映射的初始值xo,结构参数n和过渡过程参数n。作为密钥。根据密钥产生相应的混沌序列xk,yk,根据xk,yk生成相应的变换矩阵,实现对数字图像的加密。
3、混沌序列的生成
基于混沌映射厂生成混沌序列的方法主要有如下三种:
(1)实数值序列,即{xk,k=0,1,2,3,…},是混沌映射的轨迹点形成的序列;
(2)m值序列(用户自己定义的a1,a2,…,am-1,am构成),通过定义一个阀值函数Sign,由上述的实数值混沌序列经过(2)式得到:
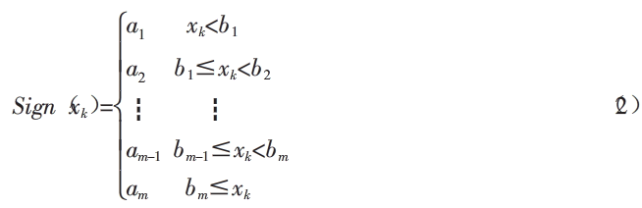
m值序列,即{Sign(xk),k=0,1,2,3,…),该序列同样具有混沌特性。
(3)比特序列,同样由实数值混沌序列得到。所不同的是,比特序列是通过对{xk,k=0,1,2,3,…}中的xk改写为L-bit的浮点形式得到。
![]()
其中bi(xk)是|xk|的第i位。所需序列为:
![]()
二、 图像加密/解密系统
基于混沌序列的图像加密方法主要分为空间域算法和频域算法。空间域算法的优点是能够充分利用图像数据的点阵特征使算法更直观,实现比较简单,且加密过程中不会引入额外的图像畸变。但如果直接应用该算法对图像逐一像素进行加密,其计算量仍然很大,特别是对一些尺寸较大的图像。另外位图经过加密后,各像素点的空间相关性被破坏,难以再进行压缩处理。基于频域的算法优势在于图像的频域空间比较稳健,抗干扰性好,而且可以将加密和压缩过程一步完成。相对于空间域算法,频域算法加密效率较高,且可以由频域的数学表达的复杂度给非法破译造成更大的困难,基于频域的图像压缩方法目前存在DCT Discrete Cosine Transformation),DWT Discrete Wavelet Transformation)等多种形式,DCT作为JPEC编码方案的重要组成部分,应用相当广泛,但DWT存在比DCT更加优异的性能,能够克服DCT的不足之处,达到更好的压缩比和图像恢复效果,并被推荐为JPEG-2000编码方案的组成部分,因此,研究基于DWT的加密技术更有应用潜力。该文根据这一思想构建基于小波变换的图像加密/解密系统,如图1,图2所示。
加密过程:如图1所示。
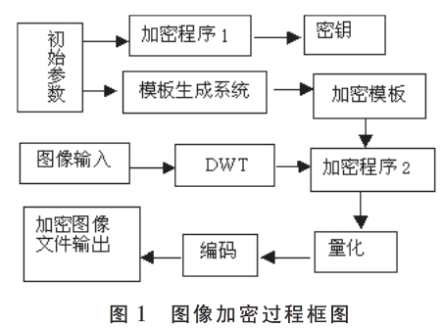
输入:原图像、参数1、参数2、参数3、…
输出:加密图像文件、密钥
步骤1:首先对于大小为M×N的任意图像,其大小可能不是8×8整数倍。这时要对原图像进行预处理,使得其大小为8×8的整数倍,其方法是在图像的边界填充0(黑色),然后对图像
进行多级小波分解,该文采用五级分解,得到小波变换系数矩阵。
步骤2:根据输入参数确定选用的混沌系统(该文选择Logistic系统),确定初始参数、选择加密模板产生方法,并输出小波系数加密模板,同时将输入参数和前两步的选择结果数据一
同输入加密程序1,经过加密处理成一个特定的密码字符串文件,提供给日后对图像信息进行解密时使用。
步骤3:根据步骤3生成的密钥模板,分别对每组小波系数进行非线形变换,得到经过加密处理的小波系数矩阵。
步骤4:将加密数据输入图像量化编码系统,进行图像数据的量化编码,输出加密图像文件,供图像信息传输与保存。
解密过程:具体过程如图2所示。
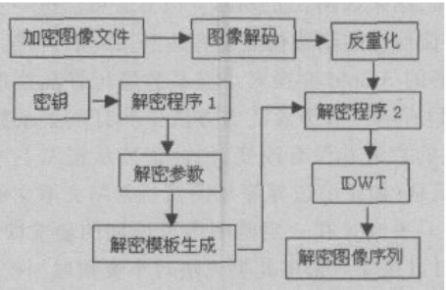
输入:加密图像文件、密钥
输出:解密图像
步骤1:首先将加密图像文件输入系统,通过图像解码、反量化处理得到经过加密的小波变换系数矩阵,供解密程序2使用;
步骤2:通过运行特定的解密程序,从载体图像中提取密钥包数据,同时进行客户端的解密程序1,得到解密参数;
步骤3:然后利用得到的参数确定解密需要的混沌系统的种类及各初始参数,生成解密模板供解密程序2使用,得到小波变换系数矩阵,进行小波逆变换,输出解密图像。
三、仿真结果与分析
为验证该系统的有效性和对加密/解密效果进行验证,该文采用Lena512灰度图像(图3a)作为实验图像,分别进行如下3个实验。

实验一、线形变换
首先利用Daubechies 9小波对Lena512图像进行5级离散小波分解(图3 )),(图3 c)分别为第一级和第二级分解的近似图像;用[1,-1]构造一个正负交替的模板,通过模板调整小波系数的正负,模板上出现-1的位置的小波系数反号。通过调整后,再进行Daubechies 9小波的五级逆变换得到重构图像(如图3d所示)。该方法实际上是引入一种周期跳变,图像的内容在一定程度上得到隐藏,但如此强烈的周期很容易让攻击者找到解密方法,使保密失去了意义。为此进一步采取一种线形增量方式,依据像素位置,逐次增大系数的倍数,同时调节系数的正负,结果如图3 e所示。
该方法虽然进一步增大了混乱程度,图像信息的隐藏仍然没有达到用户的需求。为此考虑采用非线形的Aronld变换对小波系数进行置乱处理,得到结果如图3 f所示。基于置乱的方法虽然打乱了系数的排列位置,但相应的数值并没有改变,因此仍然从密图上可以得到大量的有用信息如轮廓边界等。图像解密与文本文件的解密有不同之处,只要满足在一定范围内可识别的要求即可,少量的图像降质可以接受。采用此类方法对小波频域加密存在缺陷,无法满足高强度加密的需要。
实验二、混沌模板
采用一个混沌系统生成的密钥模板对小波系数进行非线形变换,得到结果如图3g。文章采用最简单的一维Logistic混沌系统,生成密钥模板。它的描述如下:
![]()
参数为:a=1.6,x(1))=0.4。生成离散序列X(n),序列中从n=no(其起始位置n0也作为密钥的一部分,此处no=310)开始,抽取序列A (n-no),长度与需要加密的小波系数个数相同。X(n)模板按照式(5)关系生成。
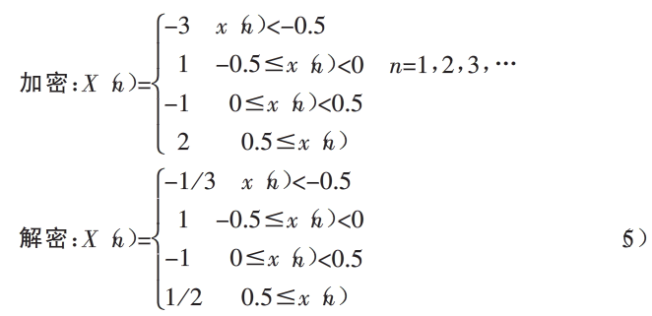
从no=310处截取密钥模板MK,将密钥模板MK与小波系数进行点乘,完成对小波系数的加密。图3g即采用Daubechies9直接对该加密系数进行IDWT变换的结果,得到一副非常混乱的Lena512密图,可见原图像信息得到有效的加密处理。
实验三、破解实验
任何一种加密方法都要经过破解实验的检验才能证明是有效的。先取a=1.6,x(1)=0.4,no=310,按照式(5)生成解密模板Mk,将解密模板Mk与加密小波系数进行点乘得到解密的小波
系数,将其进行Daubechies9的IDWT变换,得到图3h所示的一副非常清晰,与原图一致的解密图。
说明Lena图像能被有效地按照图1、图2的过程进行方便快速的加密和解密。再分别:取a=1.600001,x(1)=0.4,no=310; a=1.6,x(1)=0.400001,no=310,得到的模板Mk进行同样的IDWT变换,分别等到两副仍然十分混乱的图像图3i、图3 j。图3k是采用与图3 h相同的解密模板,进行IDWT时采用Symlets9,同样得到一副依然十分混乱的图像。可见,在解密过程中无论是混沌密钥,还是小波变换参数出现问题,均无法达到正确解密的目的。
要成功破译该文的Lena密图,其关键是要获取密钥数据文件,并从文件中成功解码,取得所有加密参数包括初始值和混沌系统的参数等。由于该文采用加密图像信息与密钥信息分开保存,并实现密钥信息的伪装和隐藏,增加密钥的获取和破解难度。
Shannon证明一次一密的密码体制是不可破的。由于每一幅加密图像对应各自不同的初始条件,所以每一幅图像就对应不同的置换关系,那种试图通过收集分析原始图像和相应加密结果信息以求寻找对应关系的努力将是徒劳的。在混沌系统中,混沌序列对初始条件具有极其敏感的依赖性,在状态空间中其轨道既非周期又不收敛,这种特性使混沌序列是不可预知、难以分析和预测。
下面假设一位攻击者已经通过某种途径得到密钥文件,他仍然需要运行特定的解密程序才能得到密钥。此处的密钥也通过混沌加密处理,具有很强的随机特性,且采用的混沌系统的初始值和参数的取值范围为整个实数域,如果采用穷举法,成功破解密钥的机会为零。
如果攻击者如果不去破解密钥,而直接对图像数据流进行解密,如果他不知道采用了变换域加密技术,破解过程根本无从谈起;更进一步,假设他知道采用何种小波变换,此时的关键技术就集中在对混沌序列的破解,该文采用混沌序列对特定位置的值进行了特殊处理,由于混沌系统的种类未确定,初始值和参数值的取值范围为整个实数域,如果攻击者采用穷举法搜索初始值和系统参数,目前还没有计算机能够完成这个任务,因此该方法具有相当高的安全性。
小知识之频域:
频域frequency domain 是描述信号在频率方面特性时用到的一种坐标系。对任何一个事物的描述都需要从多个方面进行,每一方面的描述仅为我们认识这个事物提供部分的信息。例如,眼前有一辆汽车,我可以这样描述它方面1:颜色,长度,高度。方面2:排量,品牌,价格。而对于一个信号来说,它也有很多方面的特性。如信号强度随时间的变化规律(时域特性),信号是由哪些单一频率的信号合成的(频域特性)











