admin 利用由三维Lorenz系统，Chen系统，Lü系统和一维Logistic混沌映射生成的混沌序列复合成一系列的新序列，通过这些新序列设计一个既对图像像素位置进行置乱又对图像像素值进行扰乱的图像加密系统。
一、混沌系统
本文中运用了四个混沌系统，分别是：
Logistic系统：xn+1=uxn（1-xn+1）（1），其中3.5699456…<u≤4时，系统处于混沌状态。
三个三维混沌系统Lorenz系统，Chen系统，Lü系统：
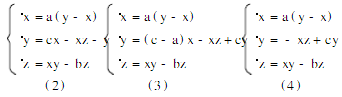
本文中Lorenz系统（2）取a=10，b=8/3，c=28，此时该系统存在混沌吸引子；Chen系统（3）取a=35，b=8，c=28，此时该系统存在混沌吸引子；Lü系统（4）取a=36，b=3，c=28，此时该系统存在混沌吸引子。
二、基于复合混沌序列的图像加密算法描述
一幅大小为M3N二维图像I，其灰度值范围是[0，255]，对这个图像进行加密。将二维图像矩阵I拉成M3N长的一维向量I′。
（1）利用Logistic映射产生内部密钥u1，v1，w1，u2，v2，w2，u3，v3，w3及其它用于图像文件加密的
复合混沌序列
。
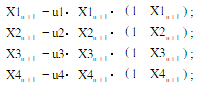
其中u1，u2，u3，u4及X10，X20，X30，X40，为外部密钥。
在计算机的实践过程中存在精度的问题，因此在计算过程中我们使用双精度数可以极大地降低出现循环数据的可能性。利用已生成的四个混沌序列分别生成chen系统，Lorenz系统，Lü系统的初始条件。
M4=mod（fix（X43M3100000），M）；每次的分组加密的像素数。
其中D1，D2…，D8，D9∈[40，100]的整数，它们作为外部密钥，E1，E2，E3用作加密序列，M4为每次的分组加密组数的序列。
将（u1，v1，w1），（u2，v2，w2），（u3，v3，w3）作为初始条件，用四阶龙格库塔法分别代人Chen系统，Lorenz系统，Lü系统进行替代，得到三维混沌序列Y1，Y2，Y3.应用这三个混沌序列得到用于加密的复合混沌序列，按如下方式复合：
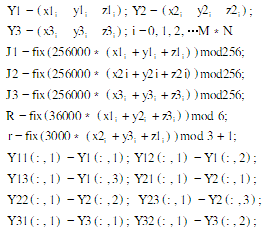
其中J1，J2，J3，E1，E2，E3为加密序列，R为对分组加密时所使用的复合混沌序列的顺序的选择序列，r为每组加密时进行异或操作次数的序列。在加密时我们不取混沌序列的初始部分，这里我们从这些混沌序列（X1，X2，X3，M4，）的第1001位开始取。Y11，Y12，Y13，Y21，Y22，Y23，Y31，Y32，Y33为用于产生位置置换序列。
（2）生成位置置换序列Position1，Position2。利用Position1完成对图像的第一次位置置换。得图像矩阵B1。
利用混沌序列X1，X2，X3产生长为fix（M3N/2）复合混沌序列XX，将序列XX排序后得到序列XX1，将XX1中元素在XX中的位置记为P1.按位置序列P1取出原图像中的这些像素点。将它们做异或运算，结果记为a1.对剩余的像素点做和运算后减去a1，将得到的值与外部密钥D1，D2…，D8，D9之和做模运算，其结果为a2。a1，a2的作用是增大算法对明文的敏感性。利用a1、a2生成复合混沌序列Z1、Z2的选择控制开关K1、K2。从Z1中选出M3N长的序列ZZ1，将其按从小到大的顺序排序后得到的序列ZZ2，将ZZ2中的元素在ZZ1中的位置序列记为Position1。按照位置置换序列Position1完成对图像的第一次位置置换，得图像矩阵B1。在Matlab7.01中的主要程序步骤如下:
aa1，aa2解密时要用为解密密钥。aa1，aa2的产生分别依赖于a1，a2，故它们也依赖于明文。
在解密时省略XX，a1，a2的生成过程，把aa1，aa2作为解密密钥直接应用。
（3）对图像矩阵B1的像素值加密，得图像矩阵B2。
对图像矩阵B1中每一组待加密的像素，先根据序列R来判定应采用哪种顺序对图像进行加密，再根据序列r来判定每组的加密操作的次数。操作完毕后得图像矩阵B2。在Matlab7.0.1中的程序步骤如下：
（4）利用a2生成复合混沌序列的选择控制开关K2，按照第二步中的方法生成位置置换序列Position2，按此矩阵完成对图像矩阵B2的第二次位置置换。得到图像矩阵B3。
（5）对图像矩阵B3的像素值加密。得到最终加密后的图像矩阵Cipher。
利用由混沌序列X1，X2，X3变换得到的序列E1，E2，E3来对图像矩阵B3的像素值加密。在Matlab7.0.1中的主要程序步骤如下：
加密过程结束。
解密过程是加密的逆过程。但解密时除了原有那些密钥外要在加入aa1，aa2作为解密密钥。
四、数值实验与安全性分析
1、密钥空间
Key=（X10，X20，X30，X40，D1，D2，D3，D4，D5，D6，D7，D8，D9），Xi0∈（0，1）i=1，…，4，Di∈[40，100]，i=1，…，9为加密密钥;并且{Xi}精确到小数点后14位;.则密钥空间约为10。而解密密钥Key=（X10，X20，X30，X40，D1，D2，D3，D4，D5，D6，D7，D8，D9，aa1，aa2）这样解密时的密钥空间就更大了。足够大的密钥空间将有效地抵抗穷举攻击。
2、对密钥的敏感性
对一幅大小为1353135的Lena图像进行加密，取密钥Key=（0.5678，0.4216，0.8936，0.1263，100，100，100，100，100，100，51，65，47）。图1（a）为原图，图1（b）为为加密后的图像。
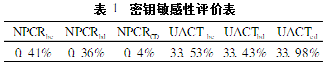
以下对密钥作如下微小变动:Key1=（0.56780000000001，0.4216，0.8936，0.1263，100，100，100，100，100，100，51，65，47），Key2=（0.5678，0.4216，0.8936，0.1263，99，100，100，100，100，100，51，65，47），用其加密后得图1（c），图1（d）。图1（e）为用解密密钥Keyd=（0.5678，0.4216，0.8936，0.1263，100，100，100，100，100，100，51，65，47，330，107）对图1（b）解密后的图像。图1（f）为用与解密密钥有微小差异的密钥Key3j=（0.5678，0.42160000000001，0.8936，0.1263，100，100，100，100，100，100，51，65，47，330，107）对图1（b）解密后的图像。由NPCRab，及UACIab可以看出此算法对密钥是很敏感的。
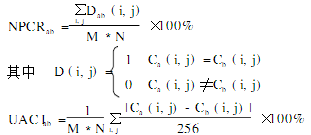
由表1可看出对密钥Key进行细微的变动后将会得到差异很大的图像。所以只有使用精确的解密密钥才能正确解密。
3、对明文的敏感性
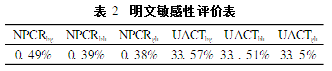
好的加密算法应该对明文很敏感，这样可以有效地抵抗差分攻击。所谓敏感性就是原图做一个微小的变动后，密文会有显著的改变。这样攻击者很难找到明文与密文之间的关系。随机选定原图像中的某个像素点，不失一般性，如像素点I（71，25），对此点的灰度值做微小修改，修改幅度为±1，对修改后的图像用密钥key加密后得图像1（g），图像1（h）。从表2中的NPCRbg，NPCRbh可以看出，对明文作了微小变动后，用相同的密钥加密得到的密文会与原密文有很大差异。这说明算法对明文非常敏感。用唯明文攻击将是徒劳的。
4、扩散性和扰乱性
我们提出了密码设计中的两个基本原则：即扩散和扰乱。对这两个特性我们这里用统计方法对图像进行分析。考察图像加密前后的直方图（图2（a），图2（b））和图像相邻像素的相关性系数。
本文先通过计算图像中所有相邻列（相邻行）的相关性系数的绝对值，在列出它们的最大值、最小值、及其平均值，见表3。
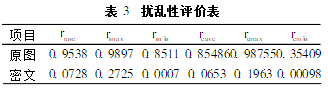相关系数定义如下：
rxy=cov（x，y）/D（x）D（y）其中cov（x，y）=E（x-E（x））（y-E（y））为协方差，D（x）为方差，x和y表示图像的灰度值。
5、抗噪声性
图像数据在传输过程中难免会遇到各种噪声，所以好的算法应该有很强的抗噪声能力。下面对密文图像分别加入大约10%的椒盐噪声和均值为6、方差是40的高斯噪声后得图3（a），图3（b），对它们解密后得到图3（c）、图3（d）。通过解密后的效果，能够看出原图大致的样子。由此可见该算法有很好的抗噪声能力。
本文提出一种基于新的复合混沌序列的加密算法，完成对图像像素位置的置乱和像素值的改变。对该算法进行安全性分析，实验结果表明：该系统有密钥空间大；对密钥和明文敏感；良好的扩散性和扰乱性等特点；同时当密文在传输过程中遇到噪声污染后，其解密后的图像效果的也不会有很大的影响。
小知识之图像加密
数字图像是目前最流行的多媒体形式之一，在政治、经济、国防、教育等方面均有广泛应用。对于某些特殊领域，如军事、商业和医疗，数字图像还有较高的保密要求。为了实现数字图像保密，实际操作中一般先将二维图像转换成一维数据，再采用传统加密算法进行加密。
