近年来,已出现了很多数字图像置乱技术,主要有:基于Arnold变换的、FASS曲线的、Hilbert曲线的、Fibonacci变换的、Gray码变换的、仿射模变换的、混沌的、矩阵变换的、行列式变换的、拉丁方的以及基于三角函数的等等。那么,我们今天就给大家介绍一种基于序列交叉变换的图像置乱加密方法。
一、序列交叉变换原理
为了方便叙述,以1,2,3,...,10为例说明:假定1,2,3,...,10是一个给定的有序序列,从中间分成两部分,采用隔位交叉对插的方法将其重新排序,经一次交叉后,序列变为6,1,7,2,8,3,9,4,10,5或1,6,2,7,3,8,4,9,5,10,称第一种方法为“内插 ”,第二种方法为“外插” 。

图1是10个数字反复进行内插的变化情况,初看起来序列似乎变得越来越乱,但经5次内插后,所得序列恰好是原序列的倒序,显然,再经5次内插后序列将恢复原序;图1也反映出各个数字的位置变化情况,内插时,1移到2的位置,2移到4的位置等等。跟踪箭头的移动,我们可以看到10个数按以下次序互相取代:1,2,4,8,5,10,9,7,3,6,1,每内插一次,这10个数就沿着上述循环过程向前推进一步。由于这一循环总共有10步,因此,经过10次内插后,各个数都回到其起始位置上。

图2是8个数的情形,由图2可看出,8个数字组成的序列在内插过程中,存在两种循环:1,2,4,8,7,5,1以及3,6,3,第一个循环每6次重复一次,第二个循环每2次重复一次。尽管循环的次数不同,但序列在内插6次后仍然被还原。
事实上位置变动都可以分为一系列的这种循环。而序列的长度是有限的,所以每个位置上的数必定能回到它先前已在过的一个位置。从这一步开始,它将重复先前的各个位置变动。但能否肯定,当一个数字第一次到达先前已到过的一个位置上时,它所到达的就是其最初的位置,答案是肯定的,因为任何内插总是可逆的。因此第一个出现重复时的位置必定是其最初位置。基于类似的理由,任何数字都不能从一个循环跳到另一个循环上。并且一旦知道有哪些循环,就可以通过一种简单的方法得出还原次数。每个循环的长度由它的步数决定:如果某一循环有n步,那么经过n次内插后就被还原。如果一个序列不止一个循环,那么还原的次数就是各循环长度的最小公倍数,经各循环长度的最小公倍数次内插后,所有数字必然回到其最初位置上。综上知,对于任何由偶数个数组成的序列,经过若干次的反复内插后,总能复原为原来的顺序。但一个序列在内插变换中有多少个循环以及各循环的步长是多少很难确定。
经研究发现,还原次数与序列长度间存在一种规律,仍以10个数为例(如表1所示)。
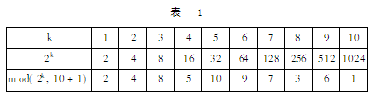
表1显示了2的各次幂以及它们被11(总长度加1)整除后所得的结果及余数。其中,2的10次方的余数为1,而使长度为10的序列复原的内插次数恰好为10。表2显示了长度为8的情形,从2的各次幂被9除所得的余数可看出。2的6次方的余数为1,而使长度为8的序列复原的内插次数也恰好是6。
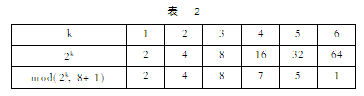
这一规律是普遍成立的,使一个序列复原所需的内插次数始终等于使2的乘方与总长度加1做取余运算时,余数恰好为1时对应的乘方数,即:序列长度n与还原次数k满足的关系为:
![]()
当n=10时,因为mod(210,10+1)=1,所以10个数字内插的还原次数为10,n取其它值时原理与此同。通过大量实验均验证了该结论的正确性,在此仅给出了一小部分数据(如表3所示)。

二、序列交叉变换原理
1、算法的实现
置乱的主要功能是将图像中像素的位置或者像素的颜色打乱,将原始图像变换成一个杂乱无章的新图像,使得图像有较低的可懂性,但为了恢复原始图像,我们必须保证置乱后图像与原始图像之间保持某种一一对应关系,为了达到较好的置乱效果,应将距离越靠近的点分布到越远的位置上,本文基于上面的原理采用如下两种实现方法:
(1)一幅数字图像,总可以通过特定的规则σ(如:FASS曲线、Hilbert曲线、Zigzag排列等)将其对应的矩阵Am#n转化为一维序列L,假设序列长度m#n为偶数,且设使序列L交叉还原的次数为k,那么实现置乱时,先序列L进行t次(t<k)交叉换位,得到新序列L,将序列L_改写为矩阵Am#n,则矩阵Am#n所对应的图像就是置乱后的图像;而当m#n为奇数时,读出序列L后,需在其最前边或最后边加入一个补偶标致数h(h[0,255]),使得序列的总长度变为偶数,其它操作与上同。但在得到的新序列L_改写为矩阵A_m#n时,需将h去掉,并记下h在L中的位置w,以便还原时使用。还原时先将Am#n转化为序列L,然后在其w处加入h,最后对所得序列进行(k-t)次交叉换位,便得到序列L,去掉h后,再按规则将L转化为矩阵B,则矩阵B所对应的图像就是还原后的图像。
(2)一幅给定的m#n的图像,也可以看成是一个m行n列组成的二维矩阵。只要分别对其各行(或列)进行交叉换位,或对所有行、列同时进行相同次数和相同方法的交叉换位,也可达到较好的置乱效果,算法也容易实现。当m#n为奇数时,可以保留一行(列)不变,也可以添加补偶行(列),原理与上同。
上述两种方法均是通过某种数学变换,使图像像素点相对位置发生变换,从而打乱原有图像有序性,实现置乱。但无论经过多么复杂的变换,图像的灰度直方图都不会发生改变。即:颜色值没有发生改变,都存在一定的缺陷:图像置乱后总体的色调没有发生变化,给破解者留下可疑迹象;&如果攻击者对像素进行重新排列,用穷举法进行破解完全只是时间的问题。为了增加置乱的效果和增加被破解的难度,可以在置乱过程中或者对置乱后的结果进行可逆灰度变换。可实现该功能的方法有很多,比较简单的方法就是:将置乱后图像的每一像素与某一数值(x)异或来实现,因为a⊕x=b,而b⊕x=a⊕x,所以x=a,但x选取太小,直方图的变化不够明显,选取太大可能会影响置乱效果,一般x选取图像像素均值左右的值,即:
![]()
2、核心伪代码

3、密码机制
为了提高置乱的安全性,在实现置乱时可与密码学相结合,可以设置密码的方法有多种,在此只给出如表3所示方式。

如可规定:q=1表示奇数,q=2表示偶数;p可为空格、逗号等;现设序列的长度为101,此时序列的总长度为奇数,故q=1,假设还原所需次数为35,位间隔标志用逗号,异或数值选用128,补偶位置为100,则密码可定为:1,35,128,100,当序列长度为偶数时不需要补偶位,但为了增大密码空间,可设置两个补偶位,补偶位对置乱的安全性有着很大的作用,一旦补偶位的位置错误,图像几乎不可能还原。因此本文算法安全性较高,还原次数也有较大的空间,加入密码生成机制后,保密空间更大,破解几乎不可能。
4、还原次数的计算
还原次数k是满足关系2k+1(mod(n+1))的最小整数解,即:k恰好是2模(n+1)的阶,当序列长度n较大时,很难用常规的方法算出k,需采用别的方法,常见的方法有:a、采用大数运算算法计算;b、通过数学方法转化求解,如采用欧拉定理;c、采用分块的方法,将大图片分解成容易计算的小块,置乱后再合拼。
三、实验结果与分析
经大量实验表明,本文加密算法置乱效果较好,限于篇幅有限,在此仅给出如图3所示的实验结果。

从实验结果可看出本文算法的置乱效果较好,经一次置乱后隐蔽性已经很强,多次置乱后效果更佳,特别是采用可逆灰度变换后,直方图发生了较大变化,图像的置乱效果明显增强,几乎看不出原图的任何信息,破解几乎不可能,但图像在置乱k/2次时会出现倒立的情形,因此在读出序列时应避免采用顺序方式,或选择图像文件加密次数时应避开k/2。
小知识之Hilbert曲线
是Hilbert作出的一条连续的,能够过单位正方形的每一个点的曲线。











