基于Baker映射迭路的图像加密算法是利用Baker映射迭路所得的有限符号串对图像像素位置编码,从而对数字图像进行置乱,并计算置乱周期和置乱度,在此基础上,利用Logistic映射的混沌性质对置乱图像作了进一步的加密。
一、相关知识
1、迭路
符号动力学指出,如果动力系统的某轨道一定通过一列不同的区间,将每个区间用一个符号对应表示,那么就得到这条轨道的迭路。
定义
设映射F是从集合X到其自身的函数,Λ为X的子集,如果:
1)若x∈Λ,则F(x)∈Λ;
2)对于任一点b∈Λ,都存在一点a∈Λ,使得F(a)=b。
则称子集Λ为F的不变集,即F(Λ)=Λ。
设函数F的不变集Λ=H0∪H1∪…∪HN,满足int(Hi)∩int(Hj)=覬,对任意的i≠j成立,其中,i,j=0,1…,N,N∈Z+.由定义,任一点x∈Λ必对所有的j∈Z满足Fj(x)∈Ht,其中t=0,1,…,N.由此可得任一点x∈Λ对应的符号串如下:
![]()
即对于所有的j∈Z,Fsj(x)∈Hsj,故x∈F-j(Hsj),且x∈∞j=-∞∩F-j(Hsj).称无限双边符号串s=…s-2s-1·s0s1s2…为点x的迭路。
定义迭标映射h:Λ→Σ为s=h(x)。
2、Baker映射
Baker映射是一个综合压缩、拉伸、翻转和折叠的映射,具有混沌的性质,受到数学家、物理学家和其他从事非线性研究的科研工作者广泛关注。下面构造的两个Bak-er映射将用于产生有限的符号串作为图像空间位置的编码。
(1)二进制Baker映射
首先考虑如式(2)、(3)所示的二进制Baker映射及其逆映射。

显然,区域Λ=[0,1]×[0,1]为式(2)、(3)的不变集.将该区域划分为两个互不相交的区域H0:[0,1]×[0,12)和H1:[0,1]×[12,1],从而得到任一点x∈Λ相应的迭标映射:
![]()
其中sj由式(1)决定,j∈Z,式(1)中取N=1.式(2)在y轴上像帐篷映射一样分段扩张,在x轴上压缩;而式(3)刚好相反,在x轴上分段扩张,在y轴上压缩,故与文献[8]中介绍的几何马蹄映射F是相似的,不同之处在于映射F的不变集ΛF是Cantor集,而式(2)、(3)的不变集Λ=[0,1]×[0,1].Robinson[8]指出,迭标映射hF:ΛF→Σ2是一一对应的。
故任一区域,int(Vs-n…s-1·s0…sn-1)=int(∩j=-(n-1)nB-j(Hsj))奂Λ(n∈Z+)都有唯一的有限符号串s-n…s-1·s0…sn-1与之对应,即对应的二进制编码(s0…sn-1,s-n…s-1)唯一,其中,sj=0,1(j=-n,…0,1,…,n-1)。这就保证用此方法对图像像素点编码是一一对应的。
(3)三进制Baker映射
可将二进制Baker映射推广到三进制,甚至是K进制的情况,并利用其迭路产生的有限符号串作为图像像素点的K进制编码.若对区域Λ=[0,1]×[0,1]从上至下划分为3等分,即H0:[0,1]×[0,13),H1:[0,1]×[13,23)和H2:[0,1]×[23,1],仍然将压缩、拉伸、翻转和折叠应用于这3个子区域,则可得到三进制Baker映射式(5)及其逆映射式(6):
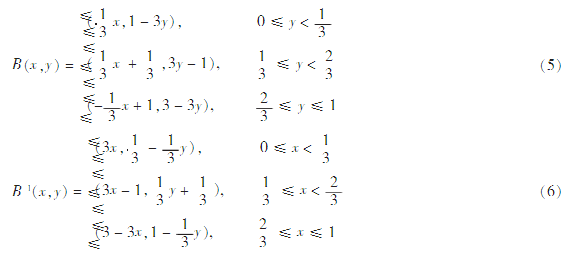
不变集仍为区域[0,1]×[0,1],式(1)中取N=2.同样用式(5)、(6)的迭路对图像像素点编码也是一一对应的。Baker映射还可有其他形式,只是式(2)和式(5)的迭路较为复杂,置乱效果较好。
二、编码过程
由于二维数字图像的像素总数总是有限的,取有限符号串即可为各像素位置编码,而编码的长度是由图像的大小所决定的。采用K进制Baker映射的迭路进行编码时,可得到KM×KM个不相交的区域int(Vs-M…s-1·s0…sM-1),其中M∈Z+,sj=0,1,…,K-1。图像大小的选取也应该是KM×KM,以保证编码是一对一的。
下面以2M×2M图像为例(M∈Z+),叙述采用二进制Baker映射的迭路编码的步骤。其中Ht的选取(t=0,1)如前面第1节所述。
步骤1
令迭代次数k=0.对于每一像素位置(i,j),读取行、列数均为n=2M的图像,取相应迭代初始点(x0,y0)=(2i-12n,2j-12n)。若点(x0,y0)∈Ht,令s0=t,其中t=0,1。
步骤2
令k=k+1,将点(xk-1,yk-1)代入式(2)得到点(xk,yk).若点(xk,yk)∈Ht,则令sk=t,其中t=0,1。
步骤3
重复步骤2,直到k=M-1。得到有限符号串s0s1s2…sM-1。令k=0。
步骤4
令k=k+1,将点(x-(k-1),y-(k-1))代入式(3)得到点(x-k,y-k).如果点(x-k,y-k)∈Ht,则令s-k=t,其中t=0,1。
步骤5
重复步骤4,直到k=M。得到有限符号串s-M…s-2s-1。
由上述步骤可得到所有像素位置的二进制编码(s0s1…sM-1,s-M…s-1),将其转换为十进制,即为(i,j)上像素的新位置。因为Vs-M…s-1·s0…sM-1=[i-1n,in]×[j-1n,jn],用于迭代的初始点满足(x0,y0)∈int([i-1n,in]×[j-1n,jn]),其中i,j=1,2,…,n,所以编码是唯一的。这就保证了图像置乱的可逆性。
三进制Baker映射(或K进制Baker映射)进行编码的步骤与上面类似,为保证编码的唯一性,选取的迭代初始点应该在int(Vs-M…s-1·s0…sM-1)中,否则若选在Vs-M…s-1·s0…sM-1边界上可能会出现迭路不唯一的情况。
三、仿真实验
1、二进制编码置乱
选用256×256的灰度LENA图像,见图1(a),作为实验对象,将其像素矩阵记为I(大小为28×28)。记置乱后的图像矩阵为I′.用第2节中编码方法为I中各像素位置(i,j)编码,并将编码转化为十进制数对(Rij,Cij),令I′(Rij,Cij)=I(i,j),即可得到置乱的图像。图1(b)~(d)为所得的置乱结果。

由图1可看出,置乱2次可达到较好的效果。表1为本算法(记为算法1)与二进制Baker映射置乱算法(记为算法2)应用于不同大小图像置乱的周期比较。

由表1可看出,算法1对于2N×2N大小的图像(N=2,3,…,10)置乱周期较算法2好.下面对256×256的LENA灰度图(图1(a))采用置乱度求法进行数值实验,绘制一个周期内两种算法置乱度的变化曲线,如图2所示。
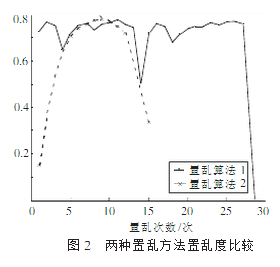
数值结果表明,算法1在一个周期内对图1(a)的置乱度较算法2稳定,迭代较少的次数即可达到较好的置乱效果,置乱周期也较长。
2、三进制编码置乱
如图3(a)选用243×243的灰度LENA图像(即大小为35×35).结合式(5)、(6),以第2节中提出的方法为I中各像素位置(i,j)编码,并将三进制编码转化为十进制数对(Rij,Cij),令I′(Rij,Cij)=I(i,j),即可得到置乱的图像I′.图3(b)~(d)为置乱结果,置乱周期达到2604。

3、灰度值扩散
为了抵抗统计分析等攻击,这里利用Logistic映射式(7)在μ取(3.5699…,4]时产生的数列处于混沌状态的特点,生成一个伪随机矩阵C,用于扩散置乱后图像的灰度值,达到加密的目的.灰度值的扩散采用按位异或,加法和取模的算法。
![]()
由式(7)的特点,选择参数μ、初始值x0和加密次数n作为密钥对图像进行加密,图像加密的具体过程如下。
步骤1采用1节提出的二进制编码置乱方法将原图像I置乱一次得到图像I′。
步骤2由式(7),取初始值x0∈(0,1),μ=4,产生一个与原图像等大的随机矩阵C(记其行数为r,列数为c),令C=floor(L·C),其中,L为该图像的灰度级。
步骤3用式(8)、(9)扩散I′的灰度值。
![]()
其中2≤i≤r,1≤j≤c,L为图像的灰度级,+表示按位异或运算。重复上述步骤k次可得到加密k次的图像I″。式(8)、(9)的逆变换为:
![]()
解密为上述过程的逆过程。图4(b)~(d)为对256×256大小的LENA灰度图加密解密结果,加密次数为3次,密钥x0=0.7123456789012345,错误解密的密钥为x0′=0.7123456789012346,可见10-16的差别就不能正确解密,密钥空间为10-16。图4(e)~(h)为加密前后对应的灰度值直方图。

图4的实验结果显示,图像文件加密后的灰度直方图能够较均匀地分布,正确解密结果与原图信息一致.随机选取图像中1000对相邻的像素,计算原图和密图的相关系数如表2所示。
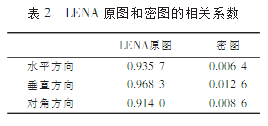 由表2可看出,该算法能够有效地削弱图像相邻点之间的相关性。
由表2可看出,该算法能够有效地削弱图像相邻点之间的相关性。
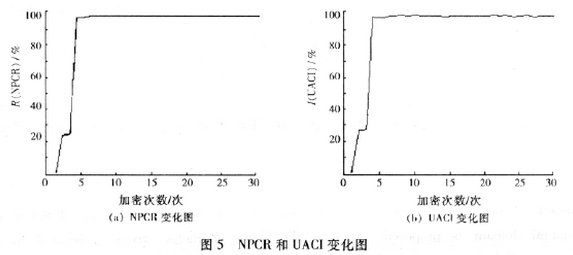
最后我们测试了明文一个像素的改变对密文的影响,图5为像素变化率NPCR和归一化平均变化强度UACI随加密次数增加的变化图。总体来看,随着加密次数增加,一个像素的改变对密文图像的影响加大。
小知识之灰度直方图
灰度直方图是灰度级的函数,它表示图像中具有某种灰度级的像素的个数,反映了图像中某种灰度出现的频率。











