基于混沌系统的加密算法成为近年来序列密码体系研究的全新领域,并出现了很多相应的加密算法。然而目前提出的混沌加密算法多是基于单一的一维或是多维混沌动力系统。前者受有限计算精度的影响,其混沌映射的动态特征在一定条件下会出现退化,影响生成序列的随机性,而且已经存在一些诸如相空间重构等较为有效的攻击方法,使其安全性不高;而后者需要通
过数值积分的方法实现加密,在实际应用中有一定难度。
为此我们提出了随机混沌动力系统组的定义。该系统组具备比单一的一维混沌系统更复杂的动力行为,且便于应用,是构造加密算法的理想工具。通过分析和实验表明,文中应用这种随机
混沌动力系统组设计的序列加密算法具有较高的安全性和扩展性。
一、随机混沌动力系统组
在加密算法提出之前,先定义几个必要的概念。
定义1:混沌动力系统组
令xi=fs(xi-1),s=0,1,…,n-1是n个不同的一维混沌动力系统,则该n个混沌动力系统构成一个混沌动力系统组模型,记为Fn,简称系统组。fs称为Fn的第s个混沌动力子系统,简称子系统。
定义2 :概率向量
定义一维向量P = (Po,P0,…,Pn-1),P的元素将[0,1]区间划分为n段:[0,Po],[p0,p1],…,[pn-2,pn一1],其中pn-1 =1,0<ps-1<ps<ps+1≤1,s=1,2,…,n-2。称P为概率向量,[Ps-i,Ps]为P的第5个概率区间,特别定义[O,p0]为第O个概率区间。
定义3:随机混沌动力系统组
对于一维概率向量P=(Po,P1,…,Pn-1)和一个系统组Fn,定义P的第s个概率区间的长度为子系统fs对应于该系统组中的概率,其中s=0,1,…,n-1,则概率向量Fn和系统组只构成一个随机混沌动力系统组,记为G(Fn,P),简称随机系统组。
引入概率向量P后,Fn就确定了每一个子系统在整个系统组中的权重,使得G( Fn,P)不仅和传统的单一混沌动力系统一样对初值xo具有敏感性,而且对p也较为敏感。进而影响到Fn的动力行为。
定义4:子系统序列
一个随机系统组G(Fn,P),对任意一个定义在有限域CF(n)={0,1,…,n-1}上的长度为L的序列RL=(r0,r1,r2,…,rl-1),都能确定凡中所有子系统的一个组合序列SRl=(fro,fri,…frl-1)。
特别地,如果有一个定义在(0,1)中的变量Pnext,Pnext每经过一次迭代,都定位到P的第s个概率区间(即Ps-1<Pnext≤ps),RL记录了Pnext。在l次迭代中每一个概率区间的序号,则将SRL简记为S,称为子系统序列。
对于一个初值xo和一个子系统的组合序列SRL=(fro,fri,…frl-1),用SR(xo)代表以下一系列运算:xi=fri-1(Xi-1)。为使xi在经过系统组中一个子系统作用后依然在下一个子系统的定义域内,可以采用例如Hash函数的方法将每个子系统的值域压缩映射到所有子系统定义域的交集D(D≠φ)上。易证,在区域D中对于任意的xi,如果都有|f'ri-1|>1,则根据混沌映射的李雅普诺夫指数的定义,可以保证SRL(X0)的李雅普诺夫指数为正,从而SRL(xo)是一个离散混沌动力系统。其中i=(1,2,…,L),L足够大。
S是G( Fn,P)所有子系统在P指导下的集合。一般地,这种集合性质的混沌系统序列保持了所有子系统的混沌特性,其动力行为比单一子系统的要复杂得多。
二、算法描述
假定明文是一个长度为L的二进制序列M= m1,m2,...mL,随机系统组G(F0,P)结合明文M生成一个子系统序列S,M在S的作用下得到密文C= c1,c2,...cL。
定义模运算T1(x)=[ax] mod 2,a=(1,+∞);[0,1]区间上的映射T2(x)。其中T1(x)的作用是将子混沌系统的生成序列由浮点数离散化为可用的二进制数,T2 (x)用于生成概率Pnext以确定下次需要迭代的子系统fP。在遵循作用不变的原则下可将T1(x)和T2(x)复杂化。
对于加密过程中生成的某个概率变量Pnext,(0≤Pnext≤1),如果有Ps-1<Pnext≤Ps或0≤Pnext≤Po,则认为Pnext确定了子系统fP =fS或fP =fo。
1、 加密及解密算法
令有限区间D’为所有子系统定义域交集D的非空子集;Lenfgth(D’)代表区间D’的长度;inf D’为区间D’的下确界。
加密算法:
1)选取迭代初值x0,x0=D’。
2)计算密文C1=T(xo)+ m1,Pnext=T2(xo+m1)。
3)分别令i =1,2,…,L-1,xi-1=(xi-1[xi-1]×Length(D’)+inf D’,计算迭代值xi=fP(Xi-1),Pnext=T2(xi+mi+1),密文Ci+1=Ti(xi)+mi+1。
4)从第2、3步依次得到密文C= c1,c2,...,cL。
解密算法与加密算法一致。
解密算法:
1)获得正确的迭代初值xo。
2)计算明文m1=T1(xo)+c1,Pnext=T2(xo+m1)。
3)分别令z =1,2,…,L-1,xi-1=(xi-1[xi-1]×Length(D’)+inf D’,计算迭代值xi=fP(Xi-1)Pnext=T2(xi+mi+1),明文mi+1=Ti(xi)= ci=+1。
4)从第2、3步依次得到明文M=m1,m2,...,mL。
加密算法的简要流程如图1所示。
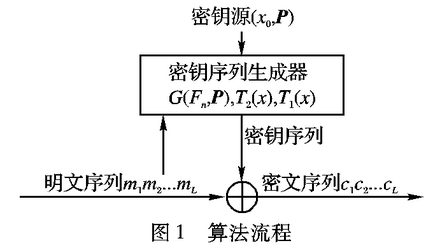
2、算法分析
由加密算法可以看出,迭代过程不仅与密钥有关,而且还与概率向量P及被加密的明文密切相关,这就使xs、P、ms+1、cs+1。四者之间关系紧密,因此分析者想要正确解密,必须知道迭代的初始值(xo;P)。即使分析者已经知道部分密文序列及其所对应的明文序列,也不可能确定之后的迭代值xs和迭代概率Pnext从而无法解密出后续部分的明文。
三、实验与分析
简单而不失普遍性,令映射T2(x)=| sin (2x)|,并选取两个混沌子系统组成系统组F2,其中fi=4x2 +12x +8,f2=4x2+ 4x,x0∈(0,1)。易知(0,1)为f1和f2定义域交集D的非空子集,且f和f2都在(0,1)上满足|f’i|>1,i=1,2。
1、敏感性测试
基于随机混沌动力系统组的加密算法使密文与初值、概率向量以及明文之间的关系非常敏感。取明文M为106位全为0的二进制序列,设初值x0=0. 33,概率向量P=(0.5,1),将M加密后的密文为C。
实验结果表明,仅当初值变化为x'0=0. 33+10-16、仅当概率向量变化为P’= (0.5+10-4,1)、仅当明文第一位发生变化时,新生成的密文和C相比,分别约有50. 05%、50. 07%、49. 97%位发生了变化。
2、统计性分析
通过该算法加密二进制明文可以得到均匀分布的密文。分别取一系列全为1或全为0的二进制序列为明文,其长度L由103位增加到106位,取密钥x0=0.33,P=(0.5,1)进行加密测试,生成的密文中O、1个数之比尺值为0. 934236~1. 07254,如图2所示。
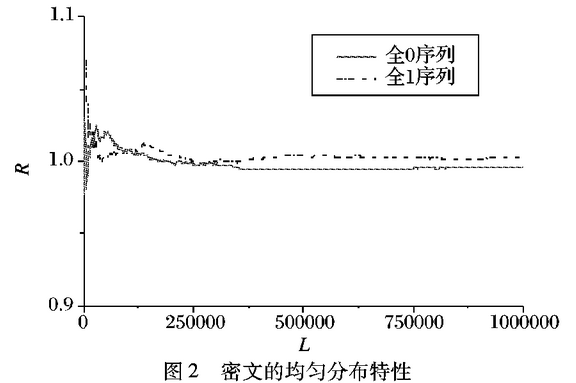
结果表明,该算法生成的密文中0、1个数几乎相等,这种均匀分布的密文可以有效抵抗统计攻击。
3、抗穷举分析
通过敏感性测试可以看到,受计算机有限精度的限制,当仅考虑初值xo时,该算法的密钥空间至少达到253;而在引入了对系统组的动力行为具有一定影响的概率向量P之后,算法的密钥空间得到进一步拓展,至少达到266。这一特点使算法可有效抵抗穷举攻击。
该算法的加密效果与系统组的复杂程度有关,即构成系统组的混沌子系统越多,且每一个子系统对应于系统组中的权重相等(即P中所有概率区间的长度都相等),加密性能就越好。故在实际应用中,可尽量选取多个混沌子系统构成系统组,使加密效果更加理想。
小知识之李雅普诺夫指数
李雅普诺夫指数指的是对初值敏感(即对混沌现象)的判断需要一个定量的指标,这个指标就是李雅普诺夫指数,它表示相邻轨线间的平均发散(分离)率,是一个统计平均量。











