基于混沌序列的幻方变换图像加密
为了图象的安全,目前有多种图像文件加密方法。那么我们今天就基于混沌序列,并结合幻方变换和镜像变换两种方法,提出了一种改进的图像加密方法。接下来,我就给大家详细的介绍一下。
一、混沌序列
混沌现象是在非线性动力系统中出现的确定性的,类似随机的过程。这种过程既非周期,又不收敛,并且对初始值有极其敏感的依赖性:
一个一维离散时间非线性动力系统定义如下:
![]()
其中,Xk=v,k=1,2,3....是一个映射,将当前状态xk映射到下一个状态xk+1,如果由初始值x0开始,反复应用t就得到一个序列{xk},k=0,1,2,3....,这一序列称为该离散时间动力系统的一条轨迹。一类非常简单却被广泛研究的动力系统是logislic映射,其定义如下:
![]()
其中,0≤u≤4称为分枝参数,xk=(0,1),当3.5699456≤u≤4时,映射工作处于混沌状态。也就是说,由初始条件x0在logislic映射的作用下所产生的序列Xk,k=1,2,3...是非周期的,不收敛的,且对初始值非常敏感。
![]()
其中λ=[0,2],λ=2时为满映射。
计算得到的logislic映射所产生的混沌序列的统计特性很有意义。
logislic序列的以上特性表明,混沌动力系统具有一定的确定性,其遍历统计特性等同于白噪声,具有形式简单对初始条件敏感等诸多特性。
二、混沌镜像加密算法
设f表示尺寸为m*n象素的一副图象并且f(x,y),0≤x≤m-1,0≤y≤n-1,表示图像f在位置f(x,y)的灰度级,算法有下面几种情况,示意如图1所示:
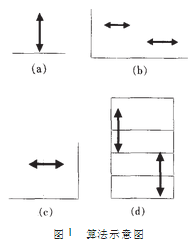
利用镜像变换,一些明文在加密后可能保持不变,如果存在太多这样的像素,明文会从加密图象里显露出来,并且,一定的时候!该算法不但不会随着加密次数增多而提高图象加密的安全性,相反,加密图象很可能恢复为原图象。
三、幻方加密算法
幻方是一个分割成若干子块的立方体结构!转动子块可以在幻方的表面上拼凑成特定的图案!也可以把拼好的图案打乱"可以对数字图象进行类似的置乱变换"一幅二维数字图象可以视为一个矩阵Im*n,矩阵中各元素ikl(k=1,2...m,l=1,2...n),表示图象中象素点(k,l)的灰度值,按照幻方的规则,对图象矩阵的各列可以同样处理,当每一行每一列都进行了一次循环移位后完成一次变换操作,得到一幅新的图象I'm*n=P(Im*n),其中,P表示从Im*n到I'm*n的映射。
幻方加密公式:
以按列循环移位为例,用一个矩阵A128*128表示128*128待加密图,通过左乘一个稀疏矩阵B128*128得到幻方加密图(矩阵表示成C),A,C看成列向量,如下:
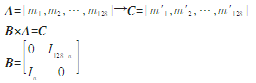
注:表示循环移位的位数I128-n,In分别表示128-n阶和n阶单位矩阵。
按行循环移位可以此类推。
幻方加密效果显著,但安全性很低,很容易遭攻击。
四、改进的加密技术
置换技术有效地打乱输入明文的次序,进而能有效地掩盖明文的统计特性,有效地抵御统计分析,可以构成sp网络的置换部件,如果结合幻方变换与混沌镜像变换两种技术,能扬长避短,无论幻方加密,还是镜像变换加密,都属于靠像素变换来实现的,两者结合是完全可行的。算法描述:
(1)由混沌系统产生第一批随机数li,i=1,2...T,T为加密次数。
(2)以li为初始值再次利用混沌系统产生第二批随机数Yi,j,并进行处理得到新的二维随机序列Xi,j(i=1,2...m,j=1,2...n)对原图按列移位!移位的位数等于Xi,j。
(3)每移一列后,对该列的每个像素作镜像变换,变换时第二次利用产生的随机序列Xi,j,设一个阈值M(如M=n/2)分两种情况处理,原图像素坐标为a(i,j),加密图像素坐标为b(i,j),变换如下:
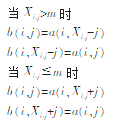
(4)将(3)中得到的图象与Yi,)异或,改变加密图的像素值的大小。
(5)回到(1)重复,直到完成T次加密。
五、模拟实验
以图2(a)待加密图做实验,(b)(c)为加密图象,加密初始值x0=0.78392;参数u=2。

图3(a)是密匙正确的解密图(b)和(c)是密匙不正确的解密图。

六、算法的统计测试
有专家曾在他的实验中对图4(a)加密,测试算法对图中像素的扩散性,下面进行同样的实验,其结果如图4(b),很明显,图4(a)中的小黑点经加密后均匀地分布到整幅图中。

还有专家提到考察加密图的直方图,图5(a),(b),(c)分别是原图,加密1次后和加密10次后的直方图。
从图5看出,加密后的直方图相当一致,且与原图的直方图大不相同。
另外,还提到考察原图与加密图相邻两点的相关性,本文分别从水平方向、竖直方向、对角线方向随机选择3000对相邻像素做同样测试,得到的数据如表1所示。
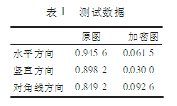
实验表明,结合幻方加密和混沌镜像加密,像素更随机地被置乱,第一次就达到很好的加密效果,且效率很高。多次加密效果更显著,实验中用到的图象大小为128*128,如果选择大小为512*512或1024*1024的图象,加密结果更理想,新算法充分利用混沌随机序列,能更有效地抗明文攻击和选择密文攻击,且该种加密方法对图象的大小要求很低,可以是M*N,不一定是N*N的正方形,更重要的,从安全角度来看,跟传统加密算法比较,本算法每轮加密的初始值不同,且每轮三次利用随机序列,随机过程增多,更安全,如果不知道密匙,要想攻破很难,所以,结合这两种技术,有着重要的实际意义。
小知识之幻方
幻方又称为魔方,方阵或厅平方,它最早起源于中国。宋代数学家杨辉称之为纵横图。











