admin 针对目前基于分数阶傅里叶变换图像加密算法的不足，我们设计了一种基于FRFT的改进图像加密新算法。算法重新设计了基于FRFT图像加密算法的流程图，将经过FRFT加密后的图像再进行置乱加密。理论分析和实验结果表明该算法在不增加算法复杂性的同时，提高了其安全性。
一、分数阶傅里叶变换理论
信号x（t）的FRFT定义为：
式中:p为FRFT的阶，可以为任意实数；α=pπ/2为FRFT的算子符号；Kp（t，u）为FRFT的变换核：
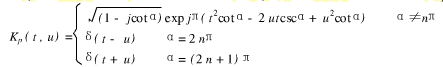
FRFT的逆变换为：
FRFT域也称为u域，而时域和频域则可视为FRFT域的特例。离散形式的分数阶傅里叶变换（DFRFT，DiscreteFractionalFourierTransform）需通过限定输入输出采样间隔来保持DFRFT变换核的正交性，从而使经过正反两次变换后得到的序列和原序列完全一致。即对FRFT的输入输出分别以间隔Δt和Δu进行取样，当FRFT域的输出采样点数M≥时域采样点数，并且采样间隔满足：
Δu_Δt=|S|_2π_sinα/M时，DFRFT可以表示为：
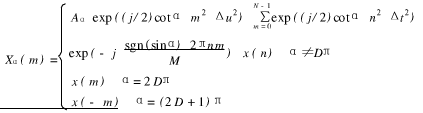
其中|S|是与M互质的整数（常取为1），
，D为整数。为了简化计算，通常取M=N，这样，当α≠Dπ时，上式可以写成如下矩阵形式：
X=Fαx
其中X=（Xα（0），Xα（1），…，Xα（N-1））T，x=（xα（0），xα（1），…，xα（N-1））T，Fα为N×N矩阵，其元素为：
同样，逆变换可以写为：
x=F-αX
其中F-α=FHα，H为共轭转置。
二、目前基于分数阶傅里叶变换的图像加密算法存在的不足
基于分数阶傅里叶变换的图像加密算法，算法将原始图像乘以随机相位掩膜后进行2DFRFT变换得到加密图像。基于分数阶傅里叶变换的指纹图像加密算法，算法中使用4次随机相位掩膜和5次FRFT变换得到加密图像。目前此类算法的安全性只取决于FRFT阶数和用户密钥生成的随机相位掩膜，所存在的不足主要有：
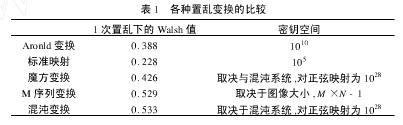
（1）密钥空间小。分数阶傅里叶变换的阶数以4为周期，其密钥空间为103，抵抗穷举攻击的能力较差；
（2）加密图像对密钥的敏感性较差。以图1为例进行说明，图1（a）为FRFT的加密图像，图1（b）为错误随机密钥下恢复的解密图像，可见即使在错误的随机相位掩膜下，仍可恢复原始图像的部分信息。
（3）加密图像的系数分布均匀性差。根据Walsh图像置乱程度评价函数，加密图像的系数分布越均匀，即加密图像的Walsh变换能量越集中左上角一点处，图像加密的效果越好。图1（c）为利用FRFT加密图像中心区域1/4系数恢复的原始图像，图1（d）为利用FRFT加密图像中心区域1/16系数恢复的原始图像。
从图中可见，只利用加密图像中很少一部分系数即可恢复出原始图像的大部分内容，即加密图像的系数分布均匀性差。
三、改进的图像加密算法
针对目前算法存在的不足，设计了一种基于分数阶傅里叶变换的改进图像加密新方案。方案的加密/解密流程图如图2所示。
加密过程描述如下：
（1）将原始图像I如图3（a）所示进行FRFT域双随机相位加密，即首先将I与随机相位掩膜MASK1=exp[i2πn（x，y）]相乘后经过阶为（α1，β1）的分数阶傅里叶变换，得到图像I′，然后将再I′与随机相位掩膜MASK2=exp[i2πh（x，y）]相乘后经过阶为（α2，β2）的分数阶傅里叶变换，其中n（x，y）和h（x，y）为用户密钥k1，k2生成的[0，1]范围内均匀分布的随机数，得到图像I″；
（2）设定初始值x0和参数μ，利用Logistic混沌映射生成置乱矩阵T（x，y），x=0，1，…，M-1;y=0，1，…，N-1，将图像I″代入下式生成最终加密图像C，其实部和虚部分别如图3（b），（c）所示。
其中t（x，y）为置乱矩阵T在（x，y）处的元素值。与其它置乱算法相比较，混沌映射具有对参数敏感以及密钥空间大等优点，其在较少置乱次数下就能达到很好的置乱效果，与其它置乱算法的比较如表1所示。
解密过程为加密过程的逆过程，为了得到原始图像I，加密图像C首先利用置乱矩阵T进行反置乱得到图像I″，然后经过阶为（-α2，-β2）的分数阶傅里叶变换后乘以随机相位掩膜MASK3=exp[-i2πh（x，y）]得到图像I′，然后再经过（-α1，-β1）的分数阶傅里叶变换后乘以随机相位掩膜MASK4=exp[-iπn（x，y）]后得到原始图像I，如图4（a）所示，其中n（x，y）和h（x，y）的生成与加密过程相同。
四、基于分数阶傅里叶变换的改进图像加密算法分析
图像加密算法的安全性取决于密钥空间的大小、加密图像对密钥的敏感性及算法的复杂性，下面逐一进行分析。
（1）密钥空间根据改进的图像加密方案，加密过程采用的密钥包括：生成随机相位掩膜中的参数k1和k2（设参数由10位数字组成，则密钥空间数量级为1010）；FRFT的阶α1，2和β1，2（密钥空间数量级为103）；混沌映射中的x0（密钥空间数量级为1015）和μ（密钥空间数量级为1013）。因此总密钥空间达到1060，可见该算法密钥空间巨大，能够抵抗非授权用户在规定时间内的穷举攻击。
（2）加密图像对密钥的敏感性设定不同的混沌映射初始条件x0和μ，其它所有参数都相同的条件下恢复的原始图像如图4（b）所示；设定用户加密密钥k1=1234567890，解密密钥k1=1234567891，其它所有参数都相同的条件下的解密图像如图4（c）所示；设定加密阶（α1=114149，β1=11751），解密阶（α1=114149，β1=11761），其它所有参数都相同的条件下的解密图像如图4（d）所示。从实验结果可以看出，密钥的细微改变都会对解密图像产生很大影响，即该算法对密钥是敏感的。
针对目前基于分数阶傅里叶变换的图像加密算法中存在的不足，设计了一种图像文件加密改进算法。算法重新设计了基于FRFT图像加密算法的流程图，将原始图像经过双随机相位加密后再进行混沌置乱映射。理论分析和模拟实验结果表明该方案不仅解决了之前算法存在的不足，而且具有密钥空间巨大、加密图像对密钥敏感等特性，是一种安全、有效的图像加密方案。
小知识之傅里叶变换
傅里叶变换能将满足一定条件的某个函数表示成三角函数（正弦和/或余弦函数）或者它们的积分的线性组合。在不同的研究领域，傅里叶变换具有多种不同的变体形式，如连续傅里叶变换和离散傅里叶变换。最初傅里叶分析是作为热过程的解析分析的工具被提出的。
