随着Internet技术与多媒体技术的飞速发展,多媒体通信逐渐成为人们进行信息交流的重要手段。与此同时,图像数据的安全性变得越来越重要。在各种不同的图像加密技术中,基于混沌理论的加密技术,正成为图像加密研究的热点。那么我们以Logistic混沌系统为基础,提出了一种新的图像加密算法,通过实验分析表明,该算法具有良好的加密性能。
一、Logistic混沌系统
混沌是一种非线性动力学规律控制的行为,表现为对初始值和系统参数的敏感性、白噪声的统计特性和区间遍历特性,具有很好的密码学特性。
一个一维离散时间非线性动力系统定义如下:
![]()
其中,xk∈V(k=0,1,2,…),称为状态;而τ:V→V是一个映射,将当前状态xk映射到下一个状态xk+1。如果从一个初始值x0开始,反复应用τ就得到一个序列{xk},k=0,1,2,…,这一序列称为该离散时间动力系统的一条轨迹。
一类非常简单却被广泛研究的动力系统是Logistic映射,其定义如下:
![]()
其中,0≤μ≤4称为分枝参数,xk∈(0,1),定义同上。混沌动力系统的研究工作指出,当3.5699456…<μ≤4时,Logistic映射工作于混沌态。也就是说,由初始条件x0在Logistic映射的作用下所产生的序列{xk},k=0,1,2,…是非周期的、不收敛的并对初始值非常敏感。对于一般的混沌映射xk+1=f(xk),概率密度ρ(x)可由Perron-Froenious方程得到,即:
![]()
当μ=4,则Logistic映射所生成的序列的概率分布函数为:
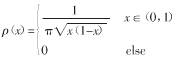
Logistic映射所产生的混沌序列轨迹点的均值是:
![]()
对于相关性,独立选取两个初始值x0和y0,则相应序列的互相关函数为:
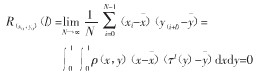
而序列的自相关函数值趋向于0,类似于δ函数,接近白噪声的特征。
Logistic序列的以上特性表明,尽管混沌动力系统具有确定性,但其遍历统计特性接近于白噪声,并具有形式简单,对初始条件敏感等诸多特性。
二、基于混沌序列的异或矩阵
1、异或矩阵的构造
由于灰度图像一般为256级,其值在0~255之间,为此,要将混沌序列做一些适当的修正,把(0,1)区间上的值映射到集{0,1,2,…,255},这可由MATLAB7.0中的floor()函数来完成,即:
![]()
其中xi是由式(1)通过迭代所得到的混沌序列,floor()函数为向负方向舍入取整函数。这样,由混沌实数列和floor()函数可得到整数序列x′1,x′2,x′3…其中xi′∈{0,1,2,…,255},i=1,2,…。
对于给定异或矩阵的大小m1×n1(m1、n1为大于1的整数)和给定的正整数k,在所得的整数列x′1,x′2,x′3…中依次选取x′k+1,x′k+2,…,x′k+m1×n1,并将它们按长度n1逐段截取,排成加密矩阵Pkm1×n1,其中pi,j∈{0,1,2,…,255},i=1,2,…,m1;j=1,2,…,n1。
2、利用异或矩阵对图像加密/解密
异或加密算法可看作如下函数:
![]()
其中,Cm1×n1为待加密矩阵,Pkm1×n1为异或矩阵,“+”为两个矩阵中对应像素值的逐比特异或运算。异或解密算法可看作如下函数:
![]()
三、基于混沌序列的置换矩阵
1、置换矩阵的构造
对于给定置换矩阵的大小m2×n2(m2、n2为大于1的整数)和给定的正整数k,在整数列x′1,x′2,x′3…中依次选取x′k+1,x′k+2,…,x′k+m2×n2,组成一个长度为m2×n2的序列,对此序列按从小到大的顺序进行排序,由各个元素位置的变化可以得到一个排序置换,此置换可以在MATLAB7.0中利用排序函数“sort()”直接得到,其长度为m2×n2,将此置换序列按长度n2逐段截取,并排成置换矩阵Zkm2×n2,其中zi,j∈{1,2,3,…,m2×n2},i=1,2,…,m2;j=1,2,…,n2。
2、置换方法置换算法
可简单地看作如下函数:
![]()
其中,Am2×n2为待加密矩阵,Zkm2×n2为置换矩阵,在Zkm2×n2中,若zi,j=r,且r=p×n2+q,则将Ap,q的值赋给Bi,j,其中i=1,2,…,m2;j=1,2,…,n2;p∈{0,1,…,m2-1},q∈{1,2,…,n2},r∈{0,1,2,…,m2×n2}。
四、基于混沌序列的图像加密/解密算法
1、加密算法算法步骤如下
(1)选取密钥K=(x0,μ0,k1,k2,m1,n1,m2,n2),其中,x0∈(0,1),3.5699456…<μ0≤4;k1、k2、m1、n1、m2、n2均为正整数,且m1与m2不能互相整除,n1与n2不能互相整除,令k=k1;
(2)对于一个图像的像素矩阵F,令M=mul(m1,m2),N=mul(n1,n2)(其中mul(x,y)表示x与y的最小公倍数),在图像矩阵的边界填充像素值255(白色),增加F的行数和列数,使它们分别是M和N的整数倍,设生成的图像像素矩阵为F1;
(3)利用密钥和Logistic映射分别产生异或矩阵Pkm1×n1和置换矩阵Zkm2×n2;
(4)将像素矩阵F1按m1×n1的大小进行分块,并利用异或矩阵Pkm1×n1进行逐块加密,将得到的加密分块再组合成像素图像,设其为F2;
(5)将像素矩阵F2按m2×n2的大小进行分块,并利用置换矩阵Zkm2×n2进行逐块置换,将得到的加密分块再组合成加密图像,设其为G;
(6)令k=k2,重复步骤(3)~(5)。
2、解密算法
解密算法是加密算法的逆运算,在解密算法中,首先令k=k2,异或矩阵与加密中的异或矩阵相同,置换矩阵是加密算法中置换矩阵的逆置换,在解密图像的过程中,先进行置换运算,再进行异或运算。
五、仿真实验及算法分析
1、仿真实验
利用MATLAB7.0软件,结合上述算法,对“lena.jpg”图像进行了加/解密的仿真实验,密钥选取为:K=(0.78354,4,10000,20000,50,50,8,8),结果如图1所示。

图1中,图像“jiamihou.jpg”为图像“lena.jpg”的加密结果,显然已看不出图像“lena.jpg”的任何信息,加密取得了较好的效果;图像“jiemihou.jpg”为对图像“jiamihou.jpg”的解密结果,通过比较得知,两个图像的像素值完全相同,说明文中提出的加密算法没有任何信息丢失;图像“cuomiyao.jpg”为x0=0.78355时的解密结果,显然,对于x0仅仅相差0.00001时,由解密结果得不到图像“lena.jpg”的任何信息,说明该算法对x0具有高度的敏感性。
2、算法分析
(1)该算法的密钥为K=(x0,μ0,k1,k2,m1,n1,m2,n2),x0可以取值于(0,1)之间的任何值,其密钥空间无穷大,μ0、k1、k2、m1、n1、m2、n2的不确定,更极大地增加了密钥空间,从而,对密钥K的穷举攻击变得不可行。
(2)算法中异或矩阵的使用,较好地增强了图像加密效果,但是异或矩阵的安全性很低,经不起唯密文攻击,更经不起已知或选择明文攻击;然而,置换矩阵对攻击者来说是未知的,故它具有较强的抗差分攻击和抗线性攻击的能力,从而较好地增强了整个算法的安全性;异或矩阵和置换矩阵的先后使用,使得整个加密算法既有较好的加密效果,又有较强的安全性。
(3)k1、k2的不同,使得两个异或矩阵各不相同,进一步增强了对图像文件加密的效果;而它们的不同也使得两个置换矩阵各不相同,从而极大地提高了整个算法的安全性。
以混沌理论为基础,文章利用Logistic混沌映射给出了一种灰度图像加密算法,通过仿真实验和分析表明,该算法具有较好的加密效果和较强的安全性。
小知识之灰度图像
灰度图像通常是在单个电磁波频谱(如可见光)内测量每个像素的亮度得到的。用于显示的灰度图像通常用每个采样像素8位的非线性尺度来保存,这样可以有256级灰度。这种精度刚刚能够避免可见的条带失真,并且非常易于编程。











