admin 混沌加密的思想自提出以后，混沌加密算法得到广泛的研究，但其中绝大多数是基于单一混沌映射系统的加密算法，如一维的Logistic映射，二维的Smale映射、Henon映射或三维的Lorenz系统等。本文在对双混沌系统应用于加密算法进行了有益的尝试和分析后，提出一种新的数据混沌加密算法——结合Cat和Logistic映射的混沌加密算法，该算法能够被应用于文件加密、实时数据流加密和商品防伪等，基于该算法的加密软件可以实现对任何类型的文件加密。
一、两种离散混沌系统：Cat映射和Logistic映射
1、Cat映射
Cat映射是一个二维的可逆混沌映射，其动力学方程的一般形式如式（1）：
由于其线性转换矩阵行列式为1，所以Cat映射又被称为是区域保留(area-preserving)的。其李雅普诺夫指数δ1，δ2为
；当a，b均为1时，就是经典的Amold Cat映射。Cat映射具有较好的混沌特性，其每次的运算首先将正方形的点空间线性拉伸，然后通过模运算分割折叠。
2、 Logistic映射
Logistic映射为自治一维离散动态系统，用一维非线性迭代函数来表征混沌行为，通过这一混沌函数可以通过微小的改变调节参数的值来产生完全不同的伪随机序列。
Logistic映射动力学方程为：
式中，μ为控制参量，μ值确定后，由任意初值X0∈(0，1)，可迭代出一个确定的时间序列。对于不同的μ值，系统（2）将呈现不同的特性，随着参数μ的增加，系统（2）不断地经历倍周期分叉，最终达到混沌。称当μ=4时由系统（2）产生的序列具有随机性、规律性、遍历性、对初值的敏感性等典型的混沌特征。
当函数在固定点的斜率的模大于等于l时，这个固定点是不稳定的，同时函数在不可忽略固定点上的梯度值越大，函数的混沌性能越好。因此有专家给出了一种改进的Logistic映射，其动力学方程为：
式中，β为[1，4]之间的一个实数，X0∈（0，1)。
二、结合Cat和Logistic映射的混沌加密算法设计
基于单一混沌系统的数字混沌加密算法，其设计的关键是对混沌映射的选择，不同的混沌映射在算法实现复杂度，算法时间和空间复杂度以及安全性等方面都有较大差异。典型的一维混沌映射有Logistic映射，其算法实现简单，运算速度较快，但密钥空间较小，安全性差，而研究较多的三维混沌Lorenz系统，其算法实现复杂，运算速度较Logistic映射慢，但密钥空间很大，安全性较高．本文所提出混沌加密算法从算法的实现、速度和安全性考虑，既能达到较小的时间和空间复杂度，又能有较大的密钥空间和较高的安全性，而且能避免单混沌系统可能出现的信息泄漏问题。算法流程图如图所示。
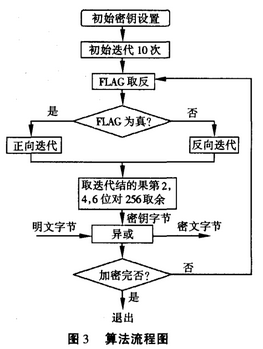
可以选定Cat映射和Logistic映射的初始值xo，y0，x’o；和3个内部参数a，b，β作为密钥，算法中设置标志FLAG: FLAG为真，正向迭代加密；FLAG为假，反向迭代加密。算法中的Xn，Yn，Xn'：为Cat映射和Logistic映射的中间迭代结果，具体加密算法如下：
①针对式（1）和（3）确定初始密钥，置FLAG为假。
②各初始迭代10次。
③FLAG取反并作如下判断：FLAG是否为真，如果为真，正向迭代；否则，反向迭代，取迭代结果的第2，4，6位对256取余，得到混沌密钥。
④将明文字节与混沌密钥字节异或，输出密文字节。
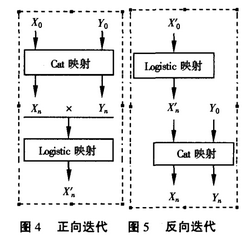
⑤判断加密完否，如果加密完则退出，否则FLAG取反，转③。其中，正向迭代如图4所示，Cat映射以茗xo，yo作为初始参数先迭代1次得到xn，yn，xn与yn乘积作为Logistic映射的参数迭代1次得到x'n作为最终迭代结果，反向迭代如图5所示，Logistic映射以x'0作为初始参数先迭代1次得到x'n，x'n与yo作为Cat映射的参数迭代1次得到xn，yn，xn与yn乘积作为最终迭代结果。
三、结合Cat和Logistic映射的混沌加密算法分析
1、 安全性分析
一个好的加密算法应该能够抵御已知的解密攻击，如选择（已知）明文攻击、惟密文攻击、统计分析攻击等．以下是对该算法所作的一些安全性分析：
*密钥空间分析
加密算法选定3个内部控制参数和3个初始状态作为密钥，密钥空间是很大的，即使在已知加密算法使用Cat映射和Logistic映射的情况下，攻击绕过穷举密钥攻击转而通过穷举间接获得3个内部控制参数也是不可能实现的，因为a，b参数的选择并没有范围限制，而β是一个在[1，4]内的实数。
*密钥敏感性分析
对Cat映射和Logistic映射的迭代初始值x0，yo，x'0分别增加10的-13次方，并观察其密钥序列，通过统计分析发现所得到的随机序列与原始随机序列平均有99.9999%不相同。
*统计学分析
根据香农理论，任何的加密密码都可以通过基于统计分析的方法来解密。加密算法的统计学特性可以通过对比加密前后的柱形图进行分析，通过分析可得：加密文本的统计学特性发生了很大的改变，如图6，图7所示。
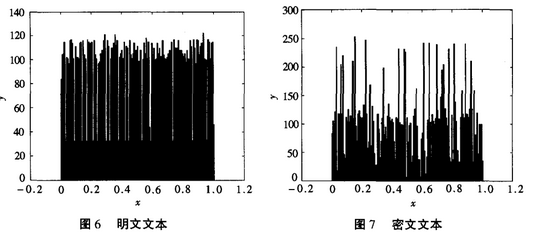
由于字符在计算机中是以补码来表示，所以当计算的值大于01111111（127）时，就变为不可显示的字符。因此在进行统计学分析时，对应的负值要加256转换为实际值进行分析。
2、性能分析
本文通过对比基于Lorenz系统的三维连续混沌加密算法进行了以下性能分析：
*时间代价
基于Lorenz系统连续混沌加密算法由于其连续数值的量化过程是一种不可逆变换，因此具有较好的安全性．但是，其需要经过数值积分，量化处理，因此运算速度较慢，不适合应用于实时性较高的场合。本算法由于采用了Cat映射和Logistic映射，其动力学方程简单，计算机处理的都是简单的基本运算，其加密速度与单纯Logistic映射加密算法相当，而且加密强度很高。
*空间代价
空间代价分为算法实现的静止空间和运行态空间．静止空间指算法变成程序后本身所占用的空间，一般表现为执行代码的长度。混沌加密算法比一般对称或不对称加密算法占有更少的静止空间，而且，由于其主要运算过程是通过迭代完成的，因此实现运行态空间运行时占用的空间很少。在空间代价上，本算法也是比较优秀的。
小知识之映射：
映射，或者射影，在数学及相关的领域还用于定义函数。函数是从非空数集到非空数集的映射，而且只能是一对一映射或多对一映射。
