admin 图象加密日益受到重视，许多加密算法被提出，其中一维混沌加密算法由于利用了混沌序列的良好复杂性、伪随机性和对初值的敏感特性而具有较好的加密性能，但与其他方法比较。其最大的缺陷是密钥空间太小，为此，我们提出了一种基于二维超混沌系统的图象文件加密方法，设计了若干个形式简单的二维超混沌模型，把它们生成的混沌序列变换成加密因子序列，采用纵横两重逐位模2加运算来加密、解密图象。
一、混沌序列与二维混沌离散系统模型
混沌（chaos）定义为：设X为一个度量空间，f：X→X称为在X上是混沌的，如果：
（1）f对初始条件的敏感依赖性：如存在 δ>0，对任何z∈X和r的任何邻域N，存在y∈N和自然数n≥0。使得d（fn（x），fn（y））>δ。
（2）f是拓扑传递的：如对任何一对开集U，yUX，存在k>0，使得fk（u）∩v≠Φ。
（3）周期点在y中稠密。
Lyapunov指数（简称李氏指数）是刻画非线性系统混沌特性的有效方法之一，李氏指数的个数与系统状态空间的维数n相同，若只有一个李氏指数大于零，则系统是混沌的；若至少有两个李氏指数大于零，则系统是超混沌的，大于零的李氏指数个数愈多，系统不稳定的程度愈高。一般来说，系统的状态量个数越多（如高维系统，对离散系统来说，n>2），它可能出现不稳定的程度会越高。
目前被广泛研究的一维混沌系统是Logistic映射，即：
其中，O≤μ≤4称为分枝参数，xk∈（0，1）。混沌动力系统的研究工作指出，当3. 569 945 6…<μ≤4.000 0时，Logistic映射工作处于混沌态。也就是说，由初始条件x0在Logistic映射的作用下所产生的序列{xk；k=0，1，2，3...）是非周期的、不收敛的并对初始值非常敏感的。
Logistic映射的另一种形式为：
其中，λ∈[0，2]，n的定义区间是（-1，1）．当1. 401 15<λ<2.000 00时，Logistic映射工作处于混沌态。
不失一般性，二维混沌离散系统有如下形式：
其中：
式中，ai（i=1，2，…，1 2）均为待定常系数。
采用高维系统产生超混沌，由于系统较之低维情况复杂，产生超混沌时序的时间增长，将有可能直接影响保密通讯实时性的要求，因此，如何在系统状态变量个数尽可能少而正性李氏指数又尽可能多的条件下，寻找到非线性形式简单的系统，是十分实际而又有意义的工作。为了寻找简单形式的二维离散超混沌系统，需进一步简化（3）式，使部分非线性项前的系数为零，然后通过计算该系统的李氏指数，即有两个或两个以上大于零的李氏指数，可认为该系统是超混沌特性的二维离散系统．通过计算，最后得到一些形式简单且具有超混沌特性的二维离散系统如表1所示。
以离散系统1为例，用它生成数字图象加密的加密变换的因子序列．先分析其简单分岔特性（如图1，图2所示），为选取合适的参数值和密钥空间做好准备。假若a5=1.3，a8= -1.1，a10=0.1先固定。
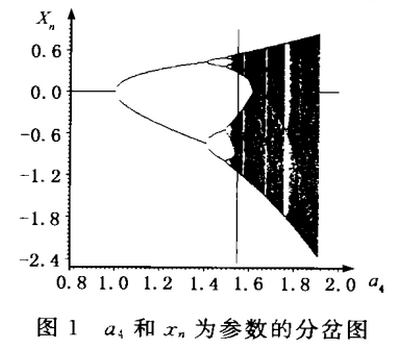
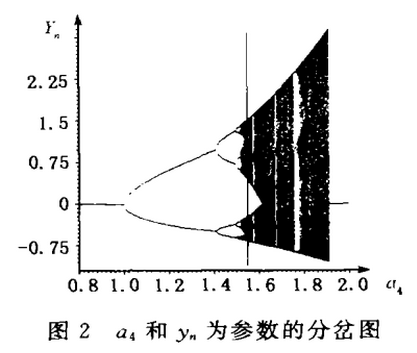
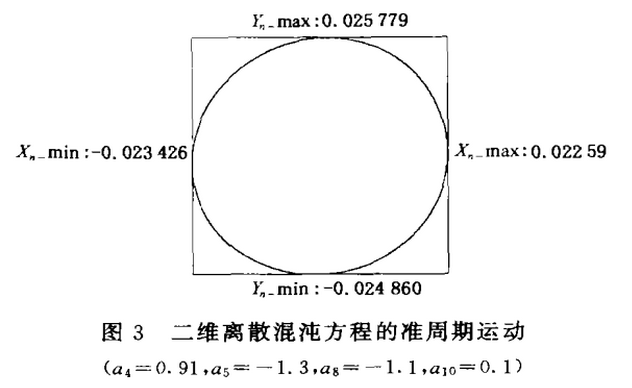
验发现a4=0.91时，离散系统1进入准周期运动（图3），而a4=1. 66时，该系统已经是超混沌态了（图4），同时可以计算出此时序列区间为-1. 577 702<xn< 0. 529 923；- 0. 634 822<yn <1. 862 664。
二、二维混沌系统应用于图象置乱加密
基于混沌序列图象加密和解密模型可以用图5表示。
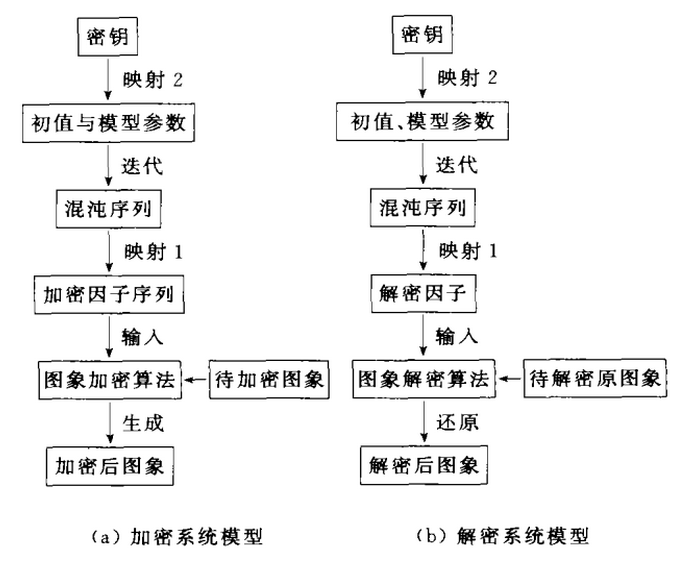显然，图象加密算法和对应的解密算法是需研究和解决的核心问题，除此之外，由混沌实数序列生成直接应用于加密变换的因子序列的变换（映射1）。以及密钥与用来决定密钥的初值和模型参数之间的映射2也是需要研究解决的问题。
映射1设计的原则是让加密因子序列尽量保持原混沌序列的伪随机性，同时适于后续加密算法的操作。目前，常用的映射1大体上分为实数值序列、位序列和二值序列3种。
（1）实数值序列，即{Xk；k=0，1，2，3...}，是混沌映射的轨迹点所形成的序列。显然不宜直接应用于加密图象，而且理论研究表明：这种无误差的平凡混沌加密方法是可破解的。
（2）位序列：同样由实数值混沌序列得到，所不同的是，位序列是通过对{Xk；k=0，1，2，3...}中的Xk改写为L-bit的浮点数形式得到的：
其中，bi（xk）是|xk|的第i位，所需序列即为bi（xk）；i=0，1，2．…．L；k=0，1，2，3…）。显然该位序列bi（xk）的取值范围是[O，9]，不适合直接作用于8bit和24bit的图象数据。
（3）二值序列，即将原混沌序列阈值化后生成的二值序列，混沌序列阈值化后，其混沌伪随机性损失较大，通过实验发现，加密后的图象轮廓依稀可见。
针对数字图象的特点，结合加密效果和效率指标要求，提出一种新的方法，即将混沌实数序列在其最大值和最小值之间，按256级等级线性映射，得到8位二进制序列，作为加密因子序列，二维超混沌模型的多个参数和两个初始条件都可以设计为密钥．由于采用的是私钥方式，为方便用户使用。
一般来说，密钥空间的连续性是首先必须保障的，如是8位密码的话，密钥最好可以从00000000～99999999连续取值，其次，从密钥到初值和（或）模型参数的映射2可以有多种形式，在此推荐分节线性变换方法，该方法既保证密钥与初值或参数的一一对应性和同步相异性（在一定计算精度范围内），又充分利用了系统可提供的密钥空间大小，更重要的是它可以有效地防止初值区间超出混沌迭代序列的区间而使密钥无效这种致命问题的出现。
以18位十进制密钥为例，它可被分为3节（长度可以相等或不等），3节分别通过线性映射，映射为用于解密的初值x0，y0，和模型参数户。
一位X的取值范围是0到9）。
基于纵横两重异或（模2加）运算的图象加密新方法，其优点是计算速度快，加密效果好，容易程序实现，可以抵御一定程度的攻击，纵横两重异或加密、解密算法描述如下：
加密算法／过程为
（1）给定需要加密的原图象，I={O≤fk（i，j）≤255，若图象为彩色图象，k=1，2，3代表3种颜色分量；若图象为灰度图象，k=1，i=O，1，2，…，M-1；j=0，1，2，…，N一1}和密钥P，图象分辨率为M×N；
（2）由密钥P映射出混沌系统的初值和模型参数；
（3）生成二维混沌序列；
（4）由实数值混沌序列通过线性变换映射到0～255的整数序列作为加密因子序列}；
（5）在横向上用生成的加密因子序列对原图象进行异或加密，对于彩色图象，每个像素的多个颜色分量可以采用同一加密因子序列或紧邻的加密因子序列加密；
（6）在纵向上用生成的加密因子序列对原图象进行异或加密；
（7）将加密后的图象在公共通道上传输；
（8）将密钥P在安全通道上传输。
解密算法／过程为：
（1）从公共通道上得到加密图象；
（2）用从安全通道上得到的密钥P；
（3）由密钥P映射出混沌系统的初值和模型参数；
（4）生成二维混沌序列；
（5）由实数值混沌序列通过线性变换映射到0～255的整数序列作为加密因子序列；
（6）在纵向上用生成的加密因子序列对原图象进行异或解密；
（7）在横向上用生成的加密因子序列对原图象进行异或解密；
（8）生成恢复后的图象。
三、实验结果
上述加密解密算法用Visual C++编程实现，分别对灰度图象和24位彩色图象加密和解密，并进行了测试，实际计算中去掉了前5 137次暂态过程，选取离散系统中的初始条件T。和yo来产生密钥，图6～图1 0给出了以离散系统1为模型的实验结果。
从实验测试结果可以看出：
（1）对图象进行X或Y单个方向的混沌加密，如图6、图7所示，可以看到：原图象的轮廓依稀可见，置乱效果欠佳．但纵横两重异或加密后，图象变得杂乱无章，置乱效果明显，有良好的保密性。
（2）由于混沌系统对初始值的敏感性，当改变密钥11415927（原密钥11415926），不但不能恢复原图象，而且还原出的图象依旧很混乱，如图8。
（3）局部破损实验中对加密后的图象进行部分破损，还原后，可以看出：破损部分没有扩散，其余部分能正确地还原，如图9所示。
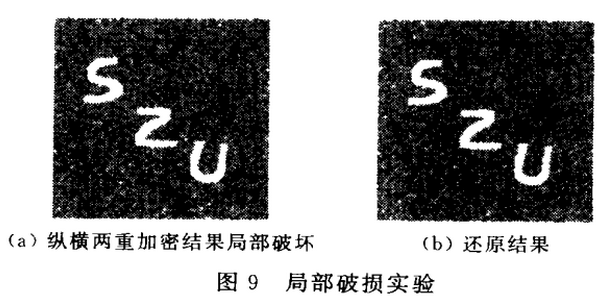
（4）从表2的加密、解密时间来看，虽然二维超混沌系统比一维系统计算复杂，但加密的速度还是相当快的。
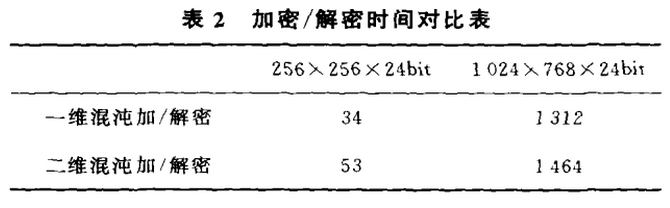
实验系统配置：CPU毒龙750r内存128MB，主频133MHZ；操作系统：Windows XP。
（5）网络传输的需要，往往会对原图象进行有损压缩（如JPEG），到达目的地后再将其转换为BMP格式，再去乱还原。如图10所示实验结果表明：压缩的品质因子quality大于5时，还原效果较好，当品质因子小于5时，去乱后的图象是不可用的。
小知识之混沌
混沌是一种确定系统中出现的无规则的运动。混沌的离散情况常常表现为混沌时间序列，混沌时间序列是由混沌模型生成的具有混沌特性的时间序列，混沌时间序列中蕴涵着系统丰富的动力学信息，混沌时间序列是混沌理论通向现实世界的一个桥梁，是混沌的一个重要应用领域。
