鉴于传统图像加密技术和低维混沌加密技术各有其局限性,我们提出了一种利用Lorenz系统产生混沌序列,并结合混沌镜像加密方法的三维超混沌图像加密方法。
一、三维Lorenz混沌系统
1、Lorenz系统
Lorenz系统是经典的三维混沌系统,以Lorenz系统生成加密混沌序列的优点在于:一是其结构较低维混沌系统复杂,产生的实数值序列更不可预测;二是系统的三个初始值和三个参数都可以作为生成加密混沌序列的种子密钥,产生的密钥空间大大高于低维混沌系统;三是对系统输出的实值混沌序列进行处理,可采用单变量或多变量组合的加密混沌序列,这样序列密码的设计更灵活。
Lorenz系统的动力学方程式为:
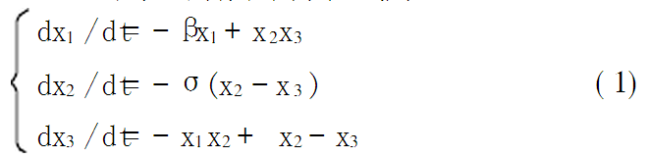
式(1)中,β,σ_,x为系统参数,典型的值为β=8/3,σ=10,x=28,在保持β,σ不变,x>24.74时Lorenz系统进入混沌状态。可用数值积分来求解微分方程(1)。采用4阶Runge-Kutta法进行求解,步长为0.01,得到随机性良好的数值序列x(n),n为数值积分算法的循环次数。Lorenz是三维混沌系统,所以得到的x(n)是一个三维的实值数组,有x1,x2,x3三个分量。
2、生成二进制序列
首先我们对Lorenz微分方程产生的实值序列进行处理,抽取二进制序列用于图像加密。定义一个量化处理的符号函数:
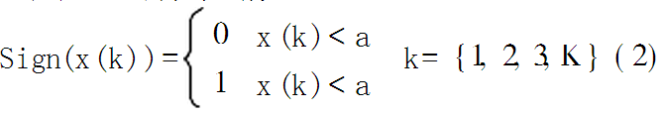
其中阈值a选取x(k)的平均值。量化后得到一个三维的二进制混沌序列:
![]()
量化处理是一个不可逆的过程,处理后的混沌序列中不包含原混沌系统的信息,因此利用混沌时间序列进行分析的攻击方法失败。
经过反复实验,下面对二进制序列性能进行分析:
(1)频数检验,用来测试序列中是否有大致相同数量的0、1,小于阈值则通过检验。
(2)序列检验,用来检验序列中出现的相同或不相同的相邻元素的概率,小于阈值则通过检验。经过反复实验,序列通过了显著水平为5%的频数检验、序列检验,由此可以证明二进制序列的随机性。如表1所示。
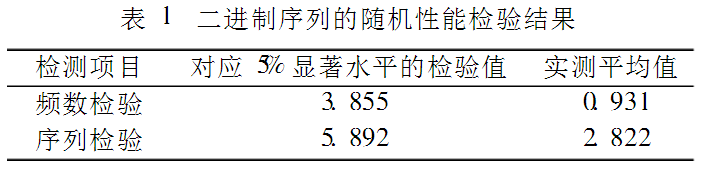
二、改进的镜像变换
镜像变换是一种十分简单的图像加密方法。混沌镜像加密算法是利用图像数据的点阵特征,由密钥产生混沌序列对图像进行加密的空间域算法。
对大小为M*N的灰度图像,定义I(x,y)为图像在(x,y)位置的灰度值,其中x#[1,M]y#[1,N]。定义置换操作swap(I(a,b),I(c,d))交换I(a,b)和I(c,d)。是否执行swap操作由密钥产生的混沌序列b(i)决定。图1所示的是一种简单的镜像变换。
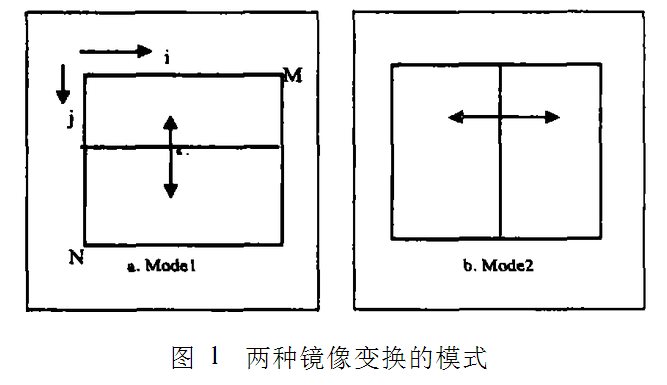
模式1中为swap(I(,ij),I(,ij+N/2)),模式2中为sawp(I(,ij),I(i+M/2,j))。可以证明运用混沌二值序列结合镜像加密的算法,可能的加密结果有21/2*M*N。例如模式一中有1/2*M*N个镜像点,每个镜像点是否置换又有两种可能性,所以可能的加密结果有21/2*M*N种。
图像进行镜像变换的关键在于镜子的位置。镜子可以水平放置,也可以垂直放置。当镜子水平放置时,同一列内的象素进行变换,当镜子垂直放置时,同一行内的象素进行变换。该文的算法采用移动镜子的位置,并以数w,q代替N/2,M/2,以加强变换的效果。
例如swap(I(,ij),I(mod(95+,i256)+1,j)),mod(,ij)为求模运算。若b(1)=1执行swap操作,这样I(1,1)与I(96,1)交换了位置。若b(96)=1执行swap操作,I(96,1)与I(195,1)互换位置,这样增加了置换复杂度,有效避免了变换的规律可循。选择w须考虑到避免循环的出现,避免I(,ij)经过一系列的变换后回到原位置的可能性。算法考虑的镜像点为M*N个,可能加密结果为2M*N。
由于Lorenz系统产生的是三维的混沌序列,单纯利用其中的一维进行加密,加密的效果并不理想。如何利用三维的混沌序列加密二维的图像矩阵成为该文所解决的问题关键。可以考虑将二维的矩阵变为三维数据,如图2所示。
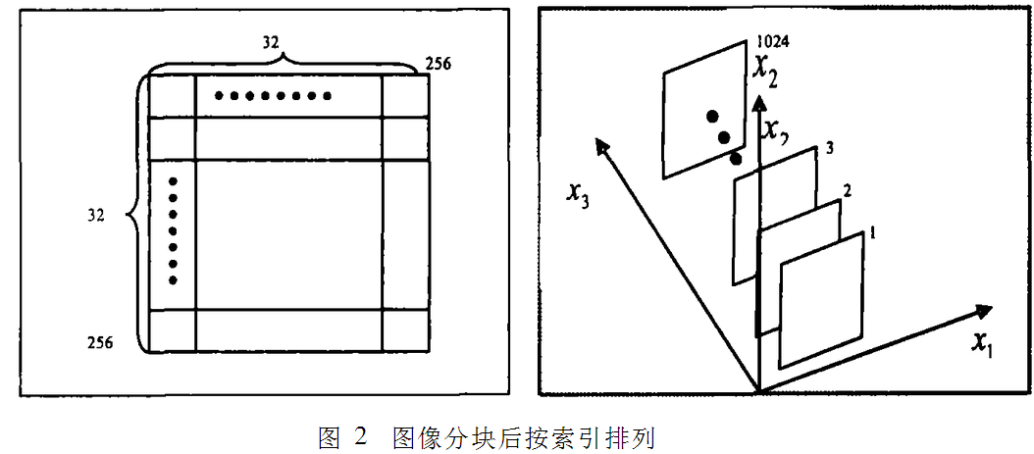
对于图像来说很容易实现,只需将M*N的图像分块,将分块的索引排列即可形成三维的数组数据。将256*256的图像分成1024个8*8的块,按照i=1,2,3__1024编号图像块的索引,并排列块。加密时在x1轴方向和x2轴方向上按上述的镜像加密规则变换,在x3轴上方法类似,只是改为对块进行操作。为保证加密效果,在x1轴和x2轴上仍对M*N的整个二维平面图像操作,而不是对块内进行镜像变换。经过x1轴x2轴x3轴三个方向的立体变换,象素置乱的范围较大,可有效抵抗基于统计的攻击。
三、基于Lorenz三维超混沌系统的图像加密算法
基于上面介绍的镜像变换和三维超混沌Lorenz系统产生的混沌序列,我们提出如下的混沌图像加密算法。
图像加密算法:
(1)输入密钥x0={1.1840;1.3627;1.2519}由Lorenz系统产生三维的混沌的实值序列x(n),n为迭代次数。
(2)实值混沌序列预处理。用量化处理的符号函数(2)经过量化处理后得到二进制伪随机序列b(k),k=1,2,3,...n。同样b(k)也是一个三维的数组。
(3)读入256*256标准的lena灰度图作为待加密的图像。开始如下变换:
*在x1轴的方向上进行变换,若b1(i)=1则将I(,ij)与I(mod(w+,i256)+1,j)互换,否则不变。
*在x2轴的方向上进行变换,若b2(i)=1则将I(,ji)与I(,jmod(q+,i256)+1)互换,否则不变。
*在x3轴的方向上进行变换,若b3(i)=1则将第i块和第(mod(r+,i1024)+1)块互换,否则不变。整数w,q,r的选取不能使变换的位置重复。算法实现中令w=18,q=89,r=105。
(4)输出加密后的图像,并在网络中传输。将密钥x0通过安全的可信赖信道传输。
图像解密算法为图像加密算法的逆过程,图像解密算法:
(1)输入解密密钥,由Lorenz系统产生三维的混沌实值序列x(n)。
(2)实值混沌序列预处理。用量化处理的符号函数(2)经过量化处理后得到二进制伪随机序列b(k),k=1,2,3,...n。
(3)读入待解密的图像。开始如下变换:
*在x3轴的方向上进行变换,若b3(i)=1则将第i块和第(mod(r+,i1024)+1)块互换,否则不变。
*在x2轴的方向上进行变换,若b2(i)=1则将I(,ji)与I(,jmod(q+,i256)+1)互换,否则不变。
*在x1轴的方向上进行变换,若b1(i)=1则将I(,ij)与I(mod(w+,i256)+1,j)互换,否则不变。
(4)得到解密后的图像,密钥正确即可恢复出原图像。密钥错误,则无法正确解密。
四、实验和结论
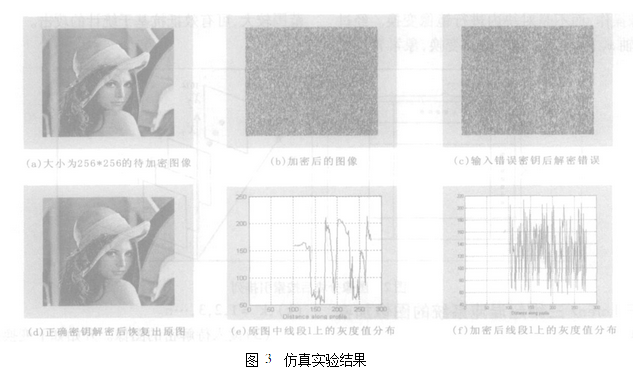
这节将验证以上提出的基于三维Lorenz系统和镜像变换的加密算法的有效性,并进行安全分析。我们对256*256的lena图像文件加密,如图3中的a所示。输入密钥{1.1840;1.3627;1.2519}后得到的密图如图3中的b所示,若用错误密钥{1.1841;1.3627;1.2519}解密后的图像为图3中的c所示。d为正确解密后恢复的原图。由此可见,即使是密钥中的一维有微小的变化,也不能正确解密出原图。图3中的e,f分别为对原图像和加密后的图像上同一位置的线段上各个象素灰度值的分布显示。由此可见,加密后将原图的灰度值分布得更均匀更随机。由上面的算法分析可知,对于M*N的图像加密后,可能的加密结果为22*M*N+1024。该算法可以有效抵抗基于统计的攻击和利用混沌时间序列进行分析的攻击方法。且算法不必利用混沌序列生成置换矩阵,只须将实值混沌序列转换为二进制的混沌序列,预处理的时间短。
小知识之二进制
二进制是计算技术中广泛采用的一种数制。二进制数据是用0和1两个数码来表示的数。它的基数为2,进位规则是“逢二进一”,借位规则是“借一当二”,由18世纪德国数理哲学大师莱布尼兹发现。当前的计算机系统使用的基本上是二进制系统。











