基于环面自同构的公钥加密算法 - 夏冰加密软件技术博客

公开密钥加密算法，也称为非对称算法，其主要特征为加密密钥与解密密钥不同，加密密钥是可以公开的，并且很难从加密密钥计算出解密密钥，所以，公钥加密算法被广泛应用，接下来，我就给大家介绍一种基于环面自同构的公钥加密算法。

一、环面自同构

环面自同构（TorusAutomorphisms）是一种典型的混沌映射，其表达式如下：

其中，A是一个形如的2×2的矩阵；a，b，c，d皆为整数；且detA=1；mod1表示只取小数部分，即xi，yi∈（0，1）。

k=a+d为A的迹，则特征多项式为f（λ）=λ2-kλ+1，其较大的一个特征值为：

当k2-4>0即k<2时（只考虑k为正），自同构A具有强烈的混沌特性。环面自同构的周期轨道，它由坐标为ξ=p1/q1，η=p2/q2的有理点组成，其中pi，qi为整数。使pi，qi互素，g为q1，q2的最小公倍数。去分母，使M成为Z2（整数向量的网格）上的映射。

因此，将映射（1）扩展到[0，N）×[0，N）上。设xi=Xi/N，yi=Yi/N，x≤Xi，Yi<N，且Xi，Yi为整数。则：

基于环面自同构的公钥加密算法

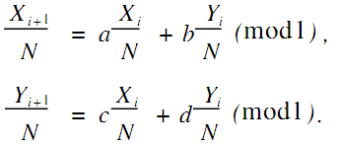
也即是：

所以，可以改写映射（1）为：

其中X，Y，N为整数，而其他参数与映射（1）要求相同。

将素数分为3类。在映射（2）中N为素数的情况下，它的周期根据这3类素数，有着3种不同类型的周期轨道。确定方式如下：

定义整数d，

其中k2-4=n2D，D为square-free。

若L（d，N）=-1，素数N为inert，映射（2）的周期为N+1的因子。若L（d，N）=1，素数N为splits，映射（2）的周期为N-1的因子。若L（d，N）=0，素数N为ramifies，若k≡2（modN），映射（2）的周期为N或1；若k≡-2（modN）则为2N或2。其中L（d，N）是勒让德符号。

二、基于环面自同构的公钥加密算法

笔者提出的公开密钥加密算法与RSA相似，其安全性都是基于大数因式分解的难度，所不同的是利用混沌映射进行迭代，并利用了该映射的周期性。

因为映射（2）是周期性的，所以：

即：

1、加密算法的描述

加密算法的描述主要分成3个部分，即密钥产生，加密和解密。

密钥产生：

（1）Alice随机选取2个大素数p和q，它们具有相同的长度；

（2）计算N=pq，φ=（p3-p）（q3-q）；

（3）随即选取整数e，使得1<e<φ，并且gcd（e，φ）=1；

（4）用欧几里德扩展算法计算d，以满足ed≡1modφ。

此时，Alice的公开密钥为（N，e），私人密钥（N，d）。加密：

1）Bob获取Alice的公开密钥（N，e）；

2）将需要加密的信息表达成整数m1，m2，且0≤m1，m2<N；

3）计算，

4）将密文ca，cb，cc，cd传送给Alice。

解密：

1）Alice接收到密文ca，cb，cc，cd；

2）计算，

3）则信息m1=pa，m2=pd。

值得注意的是，公式（4）中，矩阵中1和m1m2-1的位置是可以任意交换的，这不影响信息的加密和解密的效果。

2、加密算法的证明

设T为映射（2）的周期，即AkT+1=A（modN）。由上节可知，如果N为素数，则映射（2）的周期T可以看成（N+1）（N-1）N即N3-N的因子：

若N=p，则映射（2）的周期Tp是p3-p的因子；因为φ=（p3-p）（q3-q），Tp也就必是φ的因子。又ed=1modφ，所以ed=1+k<=1+k1Tp。因此：

Aed=A1+kφ=A1+k1Tp=A（modp）。

同理可得:

Aed=A1+kφ=A1+k2Tq=A（modq）。

根据中国剩余定理，N=pq，所以Aed=A1+kφ=A1+k′T=A（modN）。

3、简单的例子

下面举一个例子来进行说明：Alice随机选取2个大素数p=3391和q=3793，计算N=12862063，φ=2127805021604586885120。Alice选取的e=65537，通过欧几里德扩展算法计算d=36493169420076531713。Alice的公开密钥就是（N，e），私人密钥就是（N，d）。

为了加密消息m=12345674567890，Bob将消息表示为m1=1234567，m2=4567890，再使用Alice提供的公钥（N，e），根据公式（4）运算，得出ca=10495137，cb=8311873，cc=5249972，cd=10914291。Bob将密文ca，cb，cc，cd传给Alice。Alice则根据公式（5）和私人密钥（N，d）来计算出m1=1234567，m2=4567890，再将其组合成为m=12345674567890。

4、软件实现

我们所说的公钥算法步骤简洁，运算简单，与RSA相似，容易软件实现。但是需要注意的是，本加密算法的安全性基于因式分解2个大素数的乘积，在运算中需要涉及大整数的存储和运算。程序语言中提供的整数类型是不能满足需求的，所以需要单独定义。

其次，本加密算法最主要的运算就是矩阵的乘方。采用快速矩阵乘法算法将大大加快运算速度。

计算矩阵A的n次方：X=I；

for（i=n.bitsnumber（）；i>0；i--）

{

X=X2；

if（n.bitat（i）==1）

X=XA；

}

其中：n.bitsnumber（）表示取n的二进制的位数；n.bi2tat（i）则表示n的第i位的值。

三、加密算法的安全性

我们提出的叫暧昧算法与RSA有着相同的结构，因此其安全性与RSA相当。理论上，RSA的安全性取决于因式分解模n的困难性。虽然从技术上来说这是不正确的，因为在数学上至今还未证明分解模数就是攻击RSA的最佳方法，也未证明分解大整数就是NP问题。而事实上，人们设想了一些非因子分解的途径来攻击RSA体制，但这些方法都不比分解n来得容易。因此，RSA加密算法以及笔者提出的加密算法的安全性是可靠的。

在特定的条件下，RSA的实现细节的漏洞会导致对算法的攻击：选择密文攻击，公共模数攻击，低加密指数攻击以及低解密指数攻击。

RSA的选择密文攻击对笔者提出的基于环面自同构的算法是无效的。这种攻击方式主要有3种形式：明文破译、骗取仲裁签名和伪造合法签名。这3种形式都利用了指数运算保持了输入的乘积结构，也即是：