admin 随着网络技术的发展，大量的个人信息和公众信息在网上传播，信息的安全性问题成为人们关注的热点，而在信息安全中图像的安全尤为重要，那么，接下来，我就给大家介绍一种基于奇幻方的数字图像文件加密算法。
一、幻方
幻方是最古老和最流行的数字游戏之一，一个n阶幻方是由整数1，2，3...n2按下述方式组成的n×n方阵：该方阵每行、每列、每条对角线上的整数和都等于同一个数S，这个数叫幻方和。
这里介绍de laLoubere在17世纪发现的一种构造n阶幻方的方法（n为奇数）。首先将1放在最上一行的中间，其后的整数沿着自左下至右上这条对角线按照自然顺序放置，但同时须做如下调整：
1、在到达顶行时，下一个整数要放在底行，所放位置就是把底行当作顶行上边一行时该数应该放置的位置。
2、当到达最右边一行时，下一个整数要放在最左边的一列上，所放位置就是把最左边一列当作最右边那列的右边的列时该数应该放置的位置。
3、当要放置的位置上已经添好了整数，或上一个整数已经放在了幻方的右上角时，则当前要摆放的整数将放在紧挨上述位置的下方。
二、基于奇幻方的数字图像加密算法的原理
对于幻方An×n，将A中元素值为1的元素移到元素值为2的位置，将2移到元素值为3的位置，……将n×n移到1的位置，即该数组是n×n循环的。由此得到一个置换P，使A变成Ai，设A1=P(A)。设图像为In×n，将I中象素与A中的元素按行列一一对应，运用变换P，随着A变换成A1，I变成I1，从而得到置乱变换后的图像。
三、基于奇幻方的数字图像加密算法实现步骤
Step1设原图像象的数字矩阵为In×n，取幻方An×n，使An×n与In×n的元素按行列一一对应。
Step2对幻方An×n的任意元素a[i][j]，i=0，1，…n-1，j=0，1，…n-1；若其值不为1，则a[i][j]=a[i][j]-1；否则a[i][j]=nxn。
Step3记置换后的矩阵为A1，且A1=EA，对I作操作A1=EI，其中E为置换矩阵。
Step4重复Step2，Step3，经过n×n次操作后，Inxn=EnxnI=I，恢复为原图像。
四、基于奇幻方的数字图像加密算法效果分析
根据幻方生成加密算法和观察发现，众多元素按自然顺序从自左下至右上可连成众多条对角线，若将幻方矩阵看成一个正方形，它可被这些对角线填充。另外，该正方形可被分割成6大块，如图。
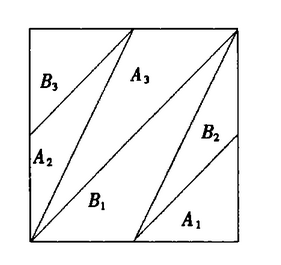
故幻方组成可概括为：按A1，A2，A3，A1的顺序循环，当A区域填充完后，对B区域按B1，B2，B3，B1的顺序循环填充，即B<A。将这六块作调整移位，可得到下图。
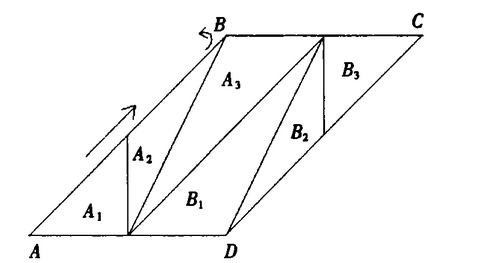该平行四边形的边由锯齿状构成；此时该平行四边形不以长度计量，以元素点计量．将它卷成圆柱（以AB为圆周），此时可看成1，2，……n×n环绕并组成柱面（类似于螺丝），如图所示。
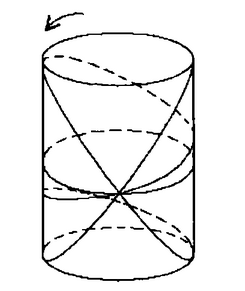
故作变换P可看成将此柱旋转，后又按原分割线还原成平行四边形，再调整移位，还原成正方形，图像发生置乱变换。
由于柱面旋转后，6大块被原来的分割线分割，故P变换不可能把图像变成点乱，而是分割成若干小块再重新组合，是块乱，加密效果不佳。
五、改进的加密算法
单独的象素点不含有任何信息，只有当众多象素点聚在一起时才有信息可言。上述幻方变换虽然移动了象素点，但相邻的点的距离没有发生变化，作变换P只是块的移动、分割和重组。
对于一幅图像，它的每一个象素点都含有信息，当隔点取走一半的象素点后，图像的信息也损失一半。
根据奇幻方的组成特点，将其中的元素按奇偶分成两列，对图像矩阵作同样分割，可得到两幅分图，每个分图的信息量为总图的一半。此时，对变换P作改进：对奇数列1，3，……n×n，将1移到3，3移到5，……，n×n移到1；对偶数列2，4，…，n×(n-1)，将n×(n-1)移到n×(n-3)，将2移到n×(n-1)，将4移到2，……；分别得到新的变换Pi，Pj。当完成上述两变换后，相邻象素点的距离发生变化，此时，幻方变换由块乱变成点乱(i，j不必相等)。算法实现步骤如下：
Stepl设原图象的数字矩阵为In×n，取幻方An×n，In×n与An×n中的元素按行列一一对应。
Step2对幻方An×n的任意元素a[i][j]，i=0，1，…n-1；j=0，1，…n-1；若其值不为1，则a[i][j]=a[i][j]-1；否则a[i][j]=nxn。
Step3对幻方An×n的任意其值为偶数的元素a[i][j]，i=0，1，…n-1；j=0，1，…n-1；若其值不为n×（n-1），则a[i][j]=a[i][j]+2；否则蛔a[i][j]=2。
Step4重复Step2后次，重复Step3 1次，记置换后的矩阵为Akl，且Akl=EklA，对I作操作Ikl=EklI，其中Ekl为变换矩阵。
六、基于奇幻方的数字图像加密算法安全性分析
上述改进的幻方加密法是将图像分成2个等信息量的分图，各自作幻方置乱变换，再合成1副图，即成为密图。可见只要有一幅分图没有还原，总图就不会还原，两幅分图各能置换出n2-1/2和n2+1/2种图像来，且两个变换之间没有联系，总图变换后可得到n2-4/4种图，比简单幻方加密所得的图像个数（n2个）增加。当n大时，要用计算机做出所有种类的图并非易事。
基于幻方置乱变换对图像进行加密，当和其他理论相结合时，如和分形也能得到好而实用的加密方法。
小知识之置乱
所谓“置乱”，就是将图像的信息次序打乱，将a像素移动到b像素的位置上，b像素移动到c像素的位置上……使其变换成杂乱无章难以辨认的图像。
