混沌系统是一种高度复杂的非线性动态系统,不仅具有对初值敏感、遍历等特性,而且还能够提供具有良好随机性、相关性和复杂性的伪随机序列。因此,将混沌系统应用到密码系统中的研究引起了国内外的广泛关注,并先后提出了许多基于混沌系统的加密算法。那么接下来,我就给大家介绍一种基于密文反馈的logistic映射认证加密算法。
基于密文反馈的logistic映射认证加密算法原理
1、伪随机序列的产生
Logistic映射是一个离散混沌系统,它的映射关系为:
![]()
混沌动力系统的研究指出,当3.5699456…<μ≤4时,logistic映射于混沌状态,为了获得二进制密钥流,需要对序列进行有限精度的A/D变换。映射产生的混沌轨道上的每个点采用二进制形式可以表示为:
![]()
式中,bi(x)可以通过式(3)得出:
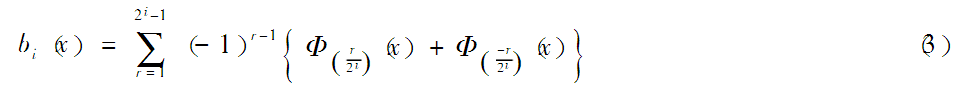
式中,Φt(x)为门限函数,即:
![]()
并且Φt(x)=1-Φt(x),通过式(1)~(4)可以得到伪随机二进制序列Bni={bi(τn(x))}∞n=0,其中,n是伪随机序列的长度,τn(x)为第n次logistic迭代时的值。
2、基于密文反馈的logistic映射认证加密算法原理
基于密文反馈的logistic映射认证加密算法主要包括以下几个步骤:
步骤1、假设A发送信息给B,明文M表示为长度tbit的明文字(这里假设为t=64,可以根据需要进行调整)。
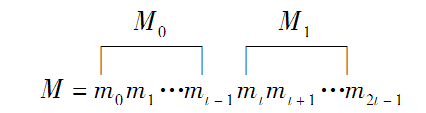
因此,第j组明文字和密文字分别可以表示为:
![]()
步骤2、将logistic映射250次,得到logistic映射产生伪随机序列的起始点τ250(x0)。
步骤3、B选择保密素数pB和qB,令nB=pBqB,并将nB公开,选择B的公钥KPB,KPB满足:
![]()
式中,gcd()表示最大公约数.A根据下图计算初值x0的模的幂运算,记为CK,然后将CK和第0组密文C0一起发送。图中,x0为logistic映射初始值;KPB、KSB为B的公钥、私钥;C0为第0组密文字;CK为利用KPB计算x0的模的幂运算。
 举例说明如下:
举例说明如下:
例1、B选择保密素数pB=7,qB=17,则nB=pBqB=7×17=119,公开nB=119;选择KPB=5作为B的公钥,KPB满足gcd(KPB,96)=gcd(5,96)=1;根据(KSBKPB)mod96=1,即(KSB×5)mod96=1,B能够计算出私钥KSB=77。设初值x0=19,A的加密过程为CK=(x0)KPB(modnB)=(19)5mod119=66,将CK发送出去;B的解密过程为x0=(CK)KSB(modnB)=(66)77_mod119=19,只有B拥有唯一的KSB,能够解密CK得到初值x0。
步骤4、同时A选择保密素数pA和qA,令nA=pAqA,并将nA公开,同理分别根据式(7)和(8)得到A的公钥和私钥KPA、KSA:

根据这个图计算签名的模的幂运算,记为CM,然后将CM附着在明文上。
 再根据下图进行加密。
再根据下图进行加密。

签名S的传输及认证过程中,S为数字签名;KPA、KSA为A的公钥、私钥;Cj为第j组密文字;CM为利用KSA计算S的模的幂运算。举例说明如下:
例2、A选择保密素数pA=7,qA=17,则nA=pAqA=7×17=119并公开nA=119;选择KPA=5作为A的公钥,KPA满足gcd(KPA,96)=gcd(5,96)=1;根据(KSAKPA)mod96=1,即(KSA×5)mod96=1,A能够计算出私钥KSA=77;设签名S=19,A的传送过程为CM=(S)KSA(modnA)=(19)5mod119=66,将CM发送出去;B的认证过程为S=(CM)KPA(modnA)=(66)77mod119=19,任何人接收到CM后,只要能够用KPA解密CM,都说明该信息是A发送的,A无法抵赖。
步骤5、通过前面所描述的方法产生二进制序列B1iB2i…B64iB65iB66i…B70i,假设第j组明文字Mj所使用的密钥字Kj=B1iB2i…B64i,计算B65iB66i…B70i序列的数值记为K'j,则第j组密文字Cj为:
![]()
式中,→表示右移运算,+表示异或运算。
步骤6、分别根据式(10)和(11)计算C'j,然后利用上面的方法产生第j+1组的密钥字Kj+1和序列数值K'j+1,即:在原有迭代基础上再迭代logistic映射70+C'j次。

步骤7、同理,第j+2组密钥字Kj+2将在第j+1组迭代基础上再迭代70+C'j+1次,此时的C'j+1为:

如果所有的明文字都已被加密,则加密过程结束,否则转到步骤5继续执行,具体实现框图如上图所示:
步骤8、解密时,B根据初值x0的传输及解密过程得到初值x0,即:
![]()
式中,KSB满足:
![]()
解密过程和加密过程类似,只需将式(9)替换为:
![]()
通过和加密相反的变换,将式(15)的等式左边序列左移K'j位,得到对应的明文字。
步骤9、由步骤8同时也分解出CM,计算模的逆运算。
![]()
根据式(16)得到签名S,与B本身计算的摘要信息对比,如果相同,则说明收到的信息是完整的,在传输过程中没有被篡改,否则就说明信息被篡改了。
考虑到实际应用中对加密系统的安全性及效率的要求,本文提出的一种基于密文反馈的logistic映射认证加密算法,不仅解决了信息传输过程中面临的信息完整性、身份认证以及防抵赖性等问题,而且适用于大量的数据文件加密。
小知识之伪随机序列
伪随机序列是具有某种随机特性的确定的序列。它们是由移位寄存器产生确定序列,然而他们却具有某种随机特性的随机序列。











