随着网络技术的发展,图像数据传输业务越来越频繁,大批的重要资料已扫描成数字化文档以二值图像的方式存储传输。给我们带来方便的同时也带来了很多安全隐患,传统的加密技术只是将其作为普通的数据流进行加密,而未考虑图像数据的特点,因此具有一定的局限性,所以图像加密技术的应用急需加强发展。
那么接下来我们就介绍一种采用混合光学模型生成混沌随机序列加密图像的方法,对加密后的图像用Walsh变换再置乱的方法来达到更高的加密强度。
一、混沌加密
近年来混沌加密技术发展十分迅速,这是由于混沌序列具有周期无限长、频谱宽等类似白噪声的特性,是理想的密码序列。这些使得混沌能很好地运用于图像加密。
本文采用混合光学双稳模型产生混沌随机序列,下面是混合光学双稳模型的迭代方程:
![]()
A和Xb是方程的系数,随着参数A和Xb的变化,系统将从同定点失稳,经倍周期分岔进入混沌,这里取A=4,Xb=2.5,此时方程处于混沌状态。
二、Walsh变换
图像置乱是利用某种算法将一幅图像各像素的次序打乱,之所以采用离散二维Walsh变换,因为与傅立叶变换相比,Walsh变换减少了存储空间并提高了运算速度,这对图像以及对其他大数据量进行实时处理是非常重要的。二维Walsh变换的定义如下:
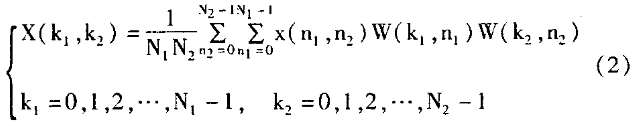
二维Walsh逆变换的定义为:
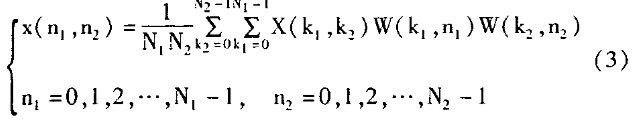
若取N1=N2=N,则二维Walsh变换的矩阵表达式为:
![]()
Walsh逆变换的表示式为:
![]()
本文运用Walsh变换,先对列进行置乱,再对行进行置乱。具体实现用哈达玛变换。哈达玛变换本质是一种特殊排序的Walsh变换,它的最大优点是它的变换核矩阵具有简单的递推关系。采用快速算法可使运算速度大大提高。
三、图像加密
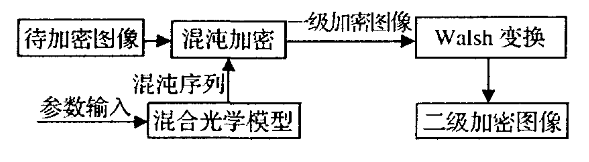
步骤1
设待加密的图像大小为N×N,首先根据输入的混沌参数利用混沌光学模型开始迭代产生混沌随机序列,序列长度为1000+N×N,将前1000个混沌数丢掉,得到大小为N×N的混沌序列。
步骤2
将生成的混沌序列N×N进行二值化处理,当Xn≥θ(θ是阈值),Yn为1,其它情况Yn为0。将二值化混沌序列与待加密的图像进行按位异或,生成置换加密后的一级加密图像。
步骤3
对一级加密图像先对列进行离散Walsh变换,再对行进行离散Walsh变换,得到二级加密像。
四、仿真结果及分析
本文的加密算法部是在Matlab7.0编程环境下实现的。
1、一级加密分析
采用256×256的图像进行。这里选取混沌映射初值X0=0.6,A=4,Xb=2.5,二值化阀值θ取不同值,对加密效果有影响。经过实验验证θ取值在θ=(2.7,3.8)的时候,生成的混沌加密图像效果较其他取值区间好。下面的两个图是不同图像内容的仿真结果。当图像内容是文字时,如上图所示;当图像内容是图像时,如下图所示。


可以看出,图像内容是图像时,θ取值范围比是文字时取值范围要小些,因此在进行混沌加密时,θ取值在θ∈(2.7,3.8)时,不管图像内容是文字还是图像都可得到较好的满足。
2、二级加密及解密分析
在一级加密图的基础上再进行Walsh变换进行置乱,采用8-256Walsh序列。下图(b)是下图(a)加密 的图像。(c)是解密与加密初值相同时,解密得到的图像。(d)是取混沌映射初值:X0=0.6,A=4,Xb=2.5,θ=3.2,8-256Walsh序列时,解密得到的图像可以看出,初值中只有一个发生很小变化,也无法解密出正确的明文。攻击者在不知混沌模型和Walsh变换的初始数据和参数时,很难猜测或者重构密钥进行解密,比传统的混沌序列有更高的加密强度。

本文将混合光学模型与Walsh变换运用于图像文件加密,比传统的混沌序列有更高的加密强度,密钥空间大,不易被破解;其次运用Walsh变换可以很大程度地节约计算时间,减小计算的复杂度。
小知识之Walsh
即在同步传输情况下,得用Walsh码作为地址码具有良好的自相关特性和处处为零的互相关特性。此外,Walsh码生成容易,应用方便。但是,Walsh码的各码组由于所占频谱带宽不同等原因,因而不能作为扩频码。











