随着分数阶傅里叶变换引入到光学系统月以后,人们开始利用混沌及分数阶傅里叶变换的相关特性对图像进行加密方面的研究。有人利用非对称双随机相位对图像进行加密,也有人使用G-S相位恢复对两幅图像加密,然而,当反变换与正变换阶数都接近时,能看到原图像的部分轮廓信息,安全性不高;为此,又有人采用了图像空间域混沌置乱和频率域分数阶傅里叶变换,来实现图像双重加密,进一步增强了安全性,扩大了密钥空间,但加密图像系数分布均匀性不好,鲁棒性不强。针对这些不足,我们设计了一种基于FRFT和混沌的图像加密算法。
一、二维离散分数阶傅里叶变换
FRFT可以解释为信号在时频平面内坐标轴绕原点逆时针旋转任意角度后构成的分数阶Fourier域上的表示方法,是Fourier变换的一种广义形式。分数阶傅里叶变换是傅里叶变换的广义形式,它表示信号从时间域到频率域变化过程中信号所呈现的特征。
对一维分数阶傅里叶变换进行推广,可以得到高维的分数阶傅里叶变换。这里简单介绍用于灰度图像加密的二维离散分数阶傅里叶变换,二维分数阶傅里叶变换的变换核为:

其中,α=p1π/2,β=p2π/2,表示信号通过二维傅里叶变换后的旋转角度。应用二维傅里叶变换核Kp1,p2(s,t,u,v),在变换阶数p1和p2给定的情况下,信号f(s,t)的二维分数阶傅里叶变换定义为:
![]()
因为二维分数阶傅里叶变换核是可分离的,即:
![]()
二维离散分数阶傅里叶变换和逆变换定义为:
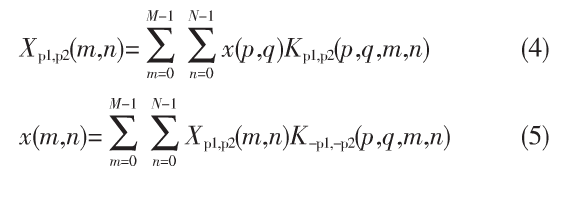
二、图像加密算法
1、混沌方程
混沌运动具有通常确定性运动所没有的几何和统计特征,如局部不稳定而整体稳定,无限自相似,连续功率谱,奇怪吸引子,分维,正的Lyapunov指数等。为了与其他复杂现象相区别,一般认为混沌系统具备随机性和初值敏感性特征。Logistic混沌映射是一个源于人口统计的动力学系统,其系统方程为:
![]()
其中xn为映射变量,μ为系统参数。当3.5699…<μ<4时,根据Lyapunov指数(λ>0)可以知道该映射处于混沌状态,3.57<μ<4称为混沌区域,其中x0∈(0,1),这样的Logistic映射定义在(0,1)上。
由于混沌系统对初值的敏感性和随机性,在给定初值和系统参数后,由混沌动力学方程对映射变量经行迭代,而最终结果成混沌状态,这个特性在图像加密领域有着广泛的应用。
2、加密算法概述
本文的加密算法主要由灰度值异或置乱、二维离散分数阶傅里叶变换和混沌置乱三个步骤组成,因此有三组密钥共同控制,实现三次加密,具体算法框图如图所示。
 本文加密算法可详细的描述为四步。
本文加密算法可详细的描述为四步。
第一步生成种子密图:设待加密图像f(x,y)大小为M×N,第一步给定x1,μ1,通过logistic混沌方程生成一个M×N长度的混沌序列,将对序列数值映射到0-255区间,并排列成为一个M×N大小的混沌图像S(x,y)。
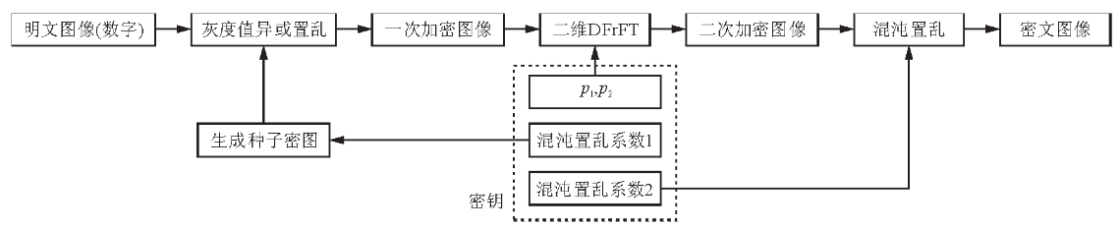
第二步将待加密图与种子密图经行灰度值异或置乱,详细算法如下:首先将S(x,y)大小扩展为(M+2)×(N+2),并将扩展位置补零,得到S′(x,y);其次将f(x,y)在x,y处的灰度值分别与S′(x,y)在该处位置的邻域八个像素点的灰度值做二进制按位异或运算;最后设有一个八位寄存器Q,将f(x,y)茌S′(x-1,y-1)结果的第一位放入Q7,f(x,y)茌S′(x-1,y)结果的第二位放入Q6,f(x,y)茌S′(x-1,y+1)结果的第三位放入Q5,以此类推,寄存器Q内数据的十进制作为第一步加密得到的密图y(x,y)在x,y处的灰度值。如图所示:
第三步,给定p1,p2对y(x,y)做二维非对称DFRFT,得到y′(x,y)。
第四步,给定x2,μ2,由混沌方程生成混沌序列,对y′(x,y)的变换系数做混沌置乱,最终得到E(x,y)。
三、加密算法仿真及结果分析
现选取大小为512*512灰度图像“lena.tif”,在MATLAB7.0中对本文加密算法进行仿真,并对仿真结果进行一系列的分析。选取二维DFRFT变换阶数p1=0.84,p2=0.63,两次混沌方程的初值x0和μ分别为经x1=0.13679275416,μ1=3.87654,x2=0.13689258527,μ2=3.96945,对原始图像文件加密后,效果见图。

1、统计特性分析
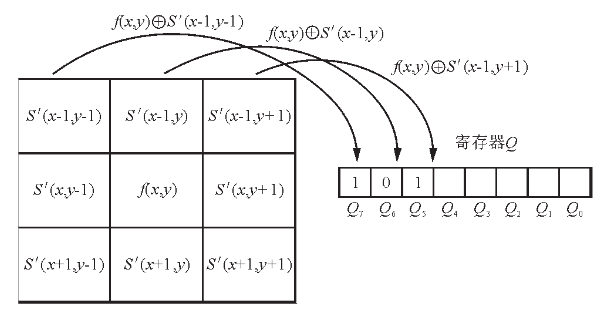
下图所示为图像加密前后的灰度直方图,由下图可以看出,明文图像的统计特性被完全打乱,在一次加密时,明文灰度值通过与混沌图片进行异或置乱后,在0-255的区间内的灰度值出现概率完全打乱,灰度直方图变的平坦。经过第二次加密,二维DFRFT将置乱后的密文映射到变换域,由于阶数的变化,空域信息不同程度的扩散到频域。然而由于DFRFT的时频效应,依然有些系数带有空域信息,因此,通过第三次混沌置乱将系数打乱,使得空频域信息完全掩盖。
当作为密钥之一的DFRFT变换阶数与正确密钥阶数误差打到0.02甚至更高时,错误解密图像与原始图像有足够大的MSE,换言之,无法辨别出原始图像。同样通过双阶数偏差的相关性,可知两个阶数同时正确,才能使得解密图像与明文图像达到最大的相关性。明文图像邻域内像素之间的性很强,而在加密后的自相关网络中可见邻域内像素间相关性极小。本算法将明文信息很好的进行了扩散和混淆,具有很强的去相关能力,对于统计特性破解有着很好的抵抗力。
2、加密算法安全性分析
从密码学角度分析本文算法的密钥空间,并考虑仿真环境MATLAB7.0的计算精度,现取8字节,15位有效数字经行分析:
在兼顾较大的MSE和相关性,阶数偏差最小达到1.0×102级别,则|pi|≈1.0×102;由于混沌系统对于初值和混沌区域μ值的敏感性,则密钥空间表示为:
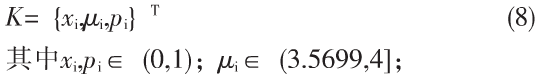
通过实验发现xi对小数点后14位,μi对小数点后6位依然敏感,即:
![]()
其中|·|表示势。因此总密钥空间为:
![]()
设破解一次需要1秒,则穷举暴力破解最长时间共需要:
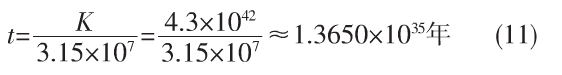
3、算法鲁棒性分析
下图是分别对通过本文算法加密后的密文进行面积12.5%和25%的遮盖或剪裁的效果图,遮盖或剪裁后使用正确密钥经行解密,仍然可以清晰的恢复出明文图像,因此该算法对遮挡或者剪裁这样的攻击具有一定的抵抗性。
将明文重新加密,对得到的密文加入方差为1,密度0.01的高斯噪声,通过正确密钥解密后,能够很好的恢复出明文信息,该算法也具有一定的抗噪能力。

本文利用DFRFT和混沌序列的特性,设计了一种图像加密算法,对算法进行了仿真,并讨论了算法的安全性。仿真结果表明,该算法密钥敏感度高,具有很大的密钥空间,抗穷举破解能力强。同时,对于密文在传输过程中的携带噪声,或者数据破损,依然具有恢复能力,算法鲁棒性较好。
小知识Fourier变换
Fourier变换能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。在不同的研究领域,傅里叶变换具有多种不同的变体形式,如连续傅里叶变换和离散傅里叶变换。最初傅里叶分析是作为热过程的解析分析的工具被提出的。











