针对现有基于混沌分组密码的图像加密算法中,扩散函数扩散速度慢、需要多轮迭代才能抵抗差分攻击的缺点,一种新的基于密文和输出混合反馈的混沌图像加密算法应运而生。该加密算法利用密文扰动混沌系统的初始值,既改善了数字混沌的退化,又能使扩散函数具有非常快的扩散速度。
一、输出和密文混合反馈混沌分组加密的设计
1、混沌加密系统设计
由于混沌系统是确定性的,混沌理论中一些工具可以用来辨别混沌系统,一旦密码分析者获得了足够的混沌轨道信息,就可能利用这些信息降低获得密码系统密钥的复杂度。输出和密文混合反馈混沌加密系统可以弥补上述缺陷,使密码分析者不能从密文,或者明文—密文对获得足够的混沌轨道来攻击加密系统。
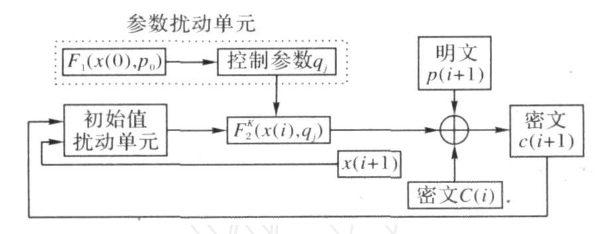
设图像像素矩阵为N=m×n。图中F1,F2都是式(2)所示的同一个混沌映射,x(0)为F1的初始值,p0为F1的参数,qj为F2的参数,q(j)=Lx(j)/2,x(j)为F1产生的混沌序列(j=1,2,…,N);p(i+1)为明文(图像的第i+1个像素值),i=1,2,…,N-1;c(i+1)为密文(加密后图像的第i+1个像素值),x(i+1)为混沌系统的输出值。
2、加密函数和解密函数
输出—密文混合反馈混沌分组密码以图像一个像素(8bit)为单位,对每一个图像的像素进行逐位异或运算,其数学表达式如下:
加密:
c(i+1)=p(i+1)+[FK((c(i)+x(i))mod(2n0-1),qj)mod256]+c(i) _ (1)
解密:
p(i+1)=c(i+1)+c(i)+[FK((c(i)+x(i))mod(2n0-1),qj)mod256] _ (2)
3、加解密步骤
加密算法步骤如下:
步骤1:密钥的产生
选择一个192bit的序列作为密钥,将这192bit分成6组,每组为32bit。将这6组比特流分别映射为6个整数:k1,k2,…,k6。
步骤2:产生扰动系统参数的序列qj(j=1,2,…,N)
令x(0)=k1,p0=k2,其中x(0)为F1的初始值,p0为F1的参数。为了保持混沌序列qj有较好的混沌特性,取F1迭代1000次以后的N个数除以2再取整得到的数作为qj序列(q1,q2,…,qN)。
步骤3:选择初始向量
将明文图像像素矩阵变为1×N的矩阵p。在F1迭代产生的序列中任意选择(比如选择迭代100次)一个数作为初始向量X,将明文图像的第一个像素p(1)与(Xmod256)进行逐位异或运算得到c(1)。
步骤4:令x(1)=k3,x(1)为F2的初始值
将x(1)、c(1)、p(i)、q(i)代入式(3),对明文图像数据进行第一轮加密,得到第一轮加密后的图像数据。
步骤5:令x(0)=k4,p0=k5,x(1)=k6
重复步骤1~4,对图像数据进行第二轮加密,在第二轮加密中步骤3略有不同,为了使加密算法对明文非常敏感,第二轮迭代必须从最后一个像素开始,然后是倒数第二个像素,最后一直到第一个像素。
步骤6:将两轮加密后的图像数据1×N,变回到m×n的图像数据矩阵
解密算法和加密算法相似,按式(2)进行。
二、基于混合反馈的混沌图像加密算法安全性分析
与其他图像加密方案相比,本加密算法具有高的安全性,能抵抗诸如已知明文攻击、统计分析、差分攻击等多种攻击,并具有大的密钥空间,更为重要的是,在具有高安全性的同时,该加密算法只需要两轮迭代,加解密速度也非常快。
1、密钥空间分析
本加密方案为192bit的加密,密钥空间达2192≈10115。本方案采用的精度是32bit,如果采用64bit精度,密钥空间可达。显然,对于如此大的密钥空间采用穷举搜索法进行攻击是不现实的。
2、密钥敏感性测试
(1)对密钥极其敏感,设加、解密密钥为:[123,456,789,369,258,147],对其中任一个子密钥,即使相差1都不能够正确解密。
(2)密钥有很小的改变所得到的加密图像有很大的差异。
3、差分攻击(明文敏感性测试)
攻击者通常会通过改变图像中很小的一点,比如只改变一个像素,来观察加密后图像的变化情况,通过这种方式,攻击者可能破解加密图像。
通过大量的实验研究证明,该加密算法实现简单,只需正反两轮迭代,就能达到高的安全性和较快的加解密速度。
小知识之混沌理论
混沌理论(Chaos theory)是一种兼具质性思考与量化分析的方法,用以探讨动态系统中(如:人口移动、化学反应、气象变化、社会行为等)无法用单一的数据关系,而必须用整体、连续的数据关系才能加以解释及预测之行为。











