目前,加密技术已经从外交和军事领域走向公开,且已发展成为一门结合数学、计算机科学、电子与通信、微电子等技术的交叉学科,使用加密技术不仅可以保证信息的机密性,而且可以保证信息的完整性和确定性,防止信息被篡改、伪造和假冒。那么,接下来我就给大家介绍一种基于分形理论的加密算法。
一、基于分形理论的加密算法_
1、分型理论
分形理论是非线性科学研究中十分活跃的一个分支,它的研究对象是自然界和非线性系统中出现的不光滑和不规则的几何形体。正是由于它的非线形,在密码学中就有了很好的用处,正如我们所熟悉的des加密需要8个s盒来完成加密的非线形一样。现拿席尔宾斯基垫片模型作为例子,对于其相似维数,r=2,N=3,Ds=log3/2,可见其维数已经不是我们常见的整数。
2、席尔宾斯基垫片模型
席尔宾斯基垫片模型开始状态为一个三角形,第一步后有3个与开始状态相似的三角形,第二步后有9个。。。第n-1步后有3的n-1次方。每个三角形有3条边,则一共有3的n次方个边。那么我们定义n为分形的形成维数。
我们定义密钥的第1位为选择的模型,第2,3,4位为分形的维数,其余位数作为控制三角形旋转的控制位。将其余位数化为二进制,0代表旋转1次,1代表旋转2次。
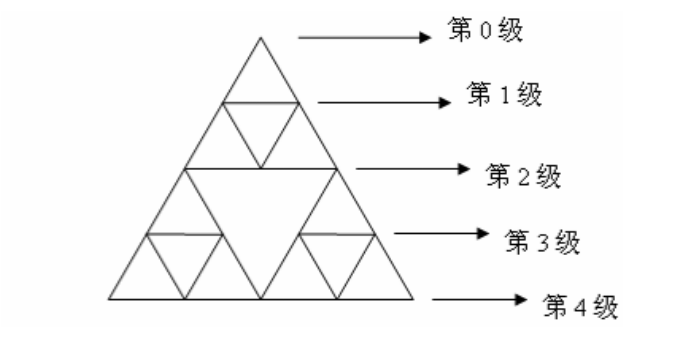
图1席尔宾斯基垫片模型
3、基于分形理论的加密算法 加密过程
假设加密密钥为0x10034567,要加密的明文为0x12345678,那么密钥第一位为1,假设1代表我们的模型是三角形。第2,3,4位为003,即维数为3,则用于加密的分形图形为上图所示。 密钥后四位的二进制为0100 0101 0110 0111,密钥控制图形成过程为:
将密钥二进制的每一位按照从上到下从左到右的顺序放在顶角朝上的小三角形中,例如将上图按照每个小三角形的高的长度作为一个等级从上到下分为5级,第0级到第1级之间有一个顶角朝上的小三角形,得到的值为0,第1级到第2级之间有两个三角形,由于在同一级则按照从左到右的顺序,得到的值为10,第2级到第3级之间有两个顶角朝上的三角形,得到的值为00,第3级到第4级之间有4个顶角朝上的三角形,得到的值为1010。形成的控制图如图所示。
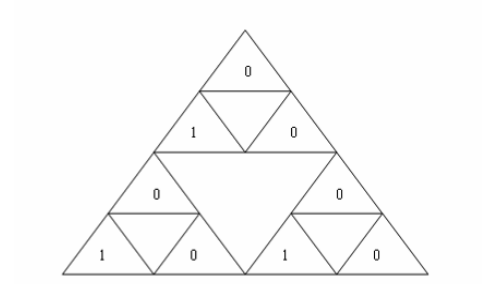
图2密钥控制图
明文的二进制为0001 0010 0011 0100 0101 0110 0111 1000,它在席尔宾斯基垫片模型中所处位置为下图所示,形成过程为:
将明文二进制的每一位按照从上到下从左到右的顺序放在顶角朝上的小三角形的三条边上。依然按照以上的规则将图1分为5级, 第0级和第1级之间有两条边,得到的值为00,第1级上有一条边得到的值为0,第1级到第2级之间有4条边,得到的值为1001,依此类推。

图3明文显示图
则明文经过密钥控制后在席尔宾斯基垫片模型中的位置如图4所示,控制规则为:在图2中如果三角形中二进制数为0的则将该三角形顺时针旋转1次,如果为1则将该三角形顺时针旋转2次。
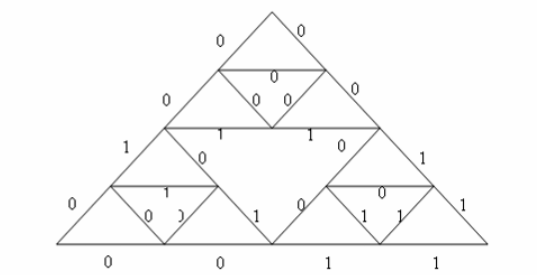
图4密文显示图
由上可知,每次加密能够加密的位数为维数的三次方(如果模型为1的话),明文中的位数有可能不是其整数倍,则继续加密规则。继续加密时,密钥循环使用,如上次用到密钥的前9位0100 0101 0,接下来使用密钥的后7位110 0111,和前2位01,依此循环使用密钥,则密钥控制图如图5所示。
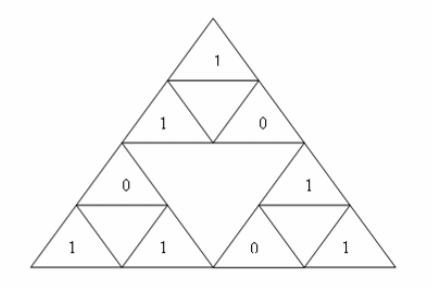
图5密钥控制图
剩下明文在席尔宾斯基垫片模型中所处位置为图6所示,明文经过密钥控制后在席尔宾斯基垫片模型中的位置如图7所示。
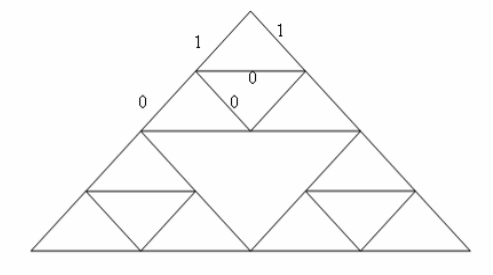
图6明文显示图
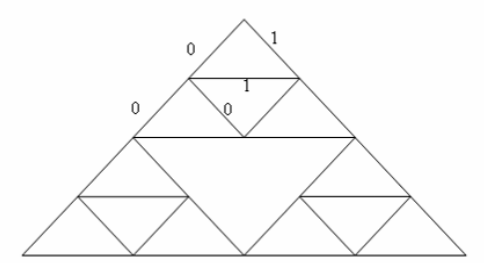
图7密文显示图
加密完成,密文按照从上到下从左到右的规则取出,得到的密文为,0000 0001 1100 1100 0010 1110 0110 1100即0x01cc2d6c。
4、基于分形理论的加密算法解密过程
解密的时候0代表三角形旋转2次,1代表1次,因为三角形旋转三次就还原了,如果是其他图形则作相应的改变。
二、基于分形理论的加密算法安全性分析
该加密方法的安全性在于:
1、第1位选择图形,如果错误则无法解出。
2、第2、3、4位为维数,过多过少的维数都会解出错误。
3、旋转的次数是根据密钥变化改变而改变,很随机。
4、未用到任何数学算法,因此根据数学公式无法作为破解的工具。
5、由于很好的非线形以及无规则性,很好的保护加密明文。
6、只有穷举法才有机会攻击,而穷举法对所有的加密方法都有效。
小知识之维数
维数(又称维度)是数学中独立参数的数目。在物理学和哲学的领域内,指独立的时空坐标的数目。我们所居于的时空有四个维(3个空间轴和1个时间轴)。我们周围的空间有3个维(上下,前后,左右)。










