基于位相抽取的三维信息加密算法 - 夏冰加密软件技术博客

近年来，加密技术不仅针对二维图像，也逐渐将三维信息纳为加密对象。三维信息加密现有的典型技术方式是数字全息术与双随机位相编码的结合。前者可以方便地记录三维信息，后者则确保了信息加密的实现。下面我就给大家介绍一种以位相抽取为基础的三维信息加密算法来实现三维信息文件加密。

一、加密算法描述

基于位相抽取的三维信息加密算法由两部分组成，第一部分是基于相位抽取的三维信息编码，这一部分是核心。

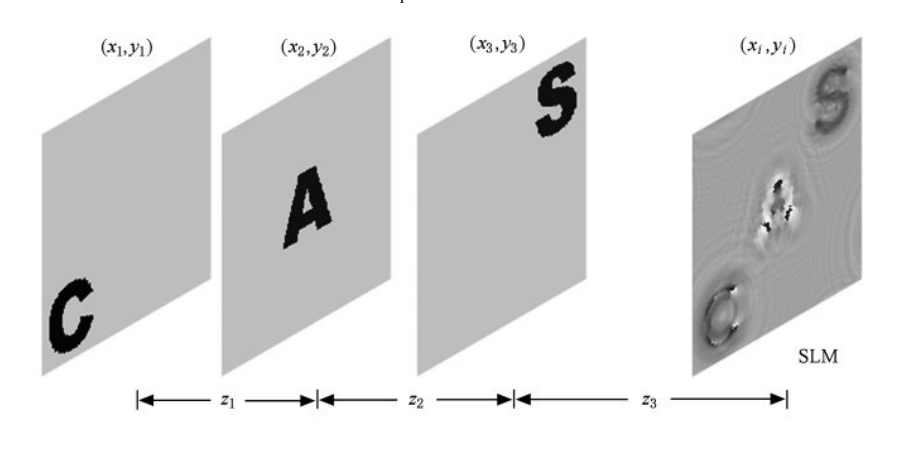
我们在计算机中构建如图的简化三维信息作为秘密信息，即位于一定纵深内的三个垂直平面上的复振幅分布。该三维信息可用一个三维函数CAS（x，y，z）表示，也可以表示为一个二维函数集合的形式｛C（x1，y1），A（x2，y2），S（x3，y3）｝。

1、加密算法

第一部分加密算法的主要目的就是将三维信息编码为二维的复振幅信息，并抽取出其位相分布函数。

具体做法如下：模拟平面波垂直入射，并依次受到三维信息复振幅调制而到达输出平面SLM（xi，yi）的衍射过程，再抽取SLM（xi，yi）的位相部分，若将波长为λ、衍射距离为z的Fresnel衍射用FrTλ，z｛.｝来表示，并且设Q（xi，yi）为抽取出的位相函数，则上述编码过程可简写为：

SLM（xi，yi）=FrTλ，z3｛FrTλ，z2｛FrTλ，z1｛C（x1，y1）｝×A（x2，y2）｝·S（x3，y3）｝，（1）

Q（xi，yi）=SLM（xi，yi）/|SLM（xi，yi）|.（2）

第二部分为Fresnel域内的双随机位相加密.在光学系统实现中，可以将抽取出的位相Q（xi，yi）加载到空间光调制器（SLM）上，并用双随机位相加密系统实施加密。通常而言，系统中的第一个随机位相板RPM1紧贴于待加密的二维信息，但由于使用了SLM，因而就允许直接将RPM1的随机位相分布与Q（xi，yi）叠加，于是只需RPM2即可达到同样目的。设RPM1和RPM2的位相函数分别为R1（xi，yi），R2（xm，ym），且密文为复振幅分布Ro（xo，yo）.为记录复振幅Ro（xo，yo），可引入一束参考光干涉得到强度分布.如不考虑参考光，且Fresnel域内SLM到RPM2和输出平面的衍射距离为分别为zⅠ，zⅡ，则第二部分算法可表示如下：

Ro（xo，yo）=FrTλ，zⅡ｛FrTλ，zⅠ｛exp［jQ（xi，yi）］×exp［jR1（xi，yi）］｝×exp［jR2（xm，ym）］｝.（3）

2、解密算法

解密过程是上述两部分加密算法的逆过程，若用IFrTλ，z｛·｝表示逆Fresnel变换，则可先得到DeSLM（xi，yi）如下：

DeSLM（xi，yi）=IFrTλ，zⅠ｛IFrTλ，zⅡ×｛exp［jRo（xo，yo）］×exp［－jR2（xm，ym）］｝×exp［－jR1（xi，yi）］｝.（4）

再经过一系列的逆Fresnel变换，就可以得到解密出的三维信息DeCAS（x，y，z），又即解密出的二维函数集合｛DeC（x1，y1），DeA（x2，y2），DeS（x3，y3）｝：

DeC（x1，y1）=IFrTλ，z1｛DeSLM（xi，yi）｝，（5）

DeA（x2，y2）=IFrTλ，z2｛DeSLM（xi，yi）｝，（6）

DeS（x3，y3）=IFrTλ，z3｛DeSLM（xi，yi）｝.（7）

可用相关系数值Co来评价解密二维函数集合的质量，从而判定三维信息的整体解密质量，Co（g，go）=cov（g，go）（σt·σto）－1，（8）

其中cov（g，go）表示解密信息g和原始秘密信息go之间的互协方差，σ为标准偏差.Co取值范围为［0，1］，其越接近1表明解密信息的质量越高。需注意的是，运用Co判定复振幅分布时，须分别对比两者的实部与虚部，或者振幅与位相。

本加密算法与系统的密钥为位相密钥和附加密钥组成。位相密钥就是第二部分加密算法中双随机位相板RPM1和RPM2的位相分布函数，附加密钥则包括波长λ和衍射距离｛zⅠ，zⅡ｝，它们共同确保了系统的安全性。

二、计算模拟与分析

1、加密过程

我们在计算机模拟中所采用的加密对象就是图中所示的三维信息“CAS”，为简单起见而又不失一般性，我们将三维信息｛C（x1，y1），A（x2，y2），S（x3，y3）｝中的A（x2，y2）取为纯振幅函数，其余两者取为纯位相函数，且除去字母覆盖区域复振幅皆为零，如图所示，其中A（x2，y2）为灰度化表示。

模拟中的波长取为632.8nm，有效采样点数为256pixels×256pixels，像素大小为8μm，衍射距离｛z1，z2，z3｝分别取为｛20，30，20｝mm。

经过基于位相抽取的三维信息编码后，SLM平面上的振幅与位相函数分布|SLM（xi，yi）|，Q（xi，yi）分别如图（a）和（b）所示，抽取SLM平面的位相分布函数Q（xi，yi）由双随机位相加密，所得到密文Ro（xo，yo）的振幅和位相分别如图（c）和（d）所示.其中，衍射距离｛zⅠ，zⅡ｝取为｛30，40｝mm。

2、解密过程

当位相密钥和附加密钥的取值正确时，按照前述解密算法首先得到解密的二维分布DeSLM（xi，yi），其振幅和位相分布分别如图（a）和（b）所示。图（b）与上图（a）对应的Co值等于1，即解密出的二维位相分布|DeSLM（xi，yi）|与原始位相分布|SLM（xi，yi）|相同。

将位相分布函数|DeSLM（xi，yi）|依相应的衍射距离进行逆Fresnel变换，可最终解密出三维信息DeCAS（x，y，z），即｛DeC（x1，y1），DeA（x2，y2），DeS（x3，y3）｝，如图（a）—（c）所示。运用数字图像处理中的形态学方法可方便地将相应的信息增强并提取出来，使相应的振幅或位相分布清晰可见.至此，计算机模拟结果证明了基于位相抽取的三维信息加密算法的有效性。