IDEA加密算法,被广泛应用于各种领。在某些特定场合,我们基于IDEA加密算法,提出了一种新颖的十进制短分组加密技术。该十进制分组密码采用IDEA密码的轮变换结构,并重新定义其中的三种基本运算以满足十进制加密的需要。与IDEA、AES、DES等分组加密算法不同的是,加解密过程中的明文、密文及各个中间状态都是等长的十进制数分组。
一、基于IDEA加密算法的十进制短分组加密算法原理
由于异或运算对十进制数没有可逆性,所以要对IDEA加密算法中的运算进行重新设计。考虑到加密算法对十进制数的可逆性,同时保证加密算法的性能,此算法采用十进制模加运算、十进制模乘运算和十进制数异或运算三种基本运算。加密算法可以对8位、16位、32位和64位四种长度的十进制明文分组进行加解密,密钥取相应明文长度的两倍。下面我们就以32位长度的明文分组为例,讨论此加密算法的实现原理。
1、加密算法中的三种运算
由于IDEA加密算法中的三种运算:二进制的异或运算、模216整数加法、模216+1整数乘法对十进制数不再适用,所以要对IDEA加密算法中的运算进行重新设计。
(1)十进制模加运算+
十进制模加运算记为+。本文采用模100000000加法。
(2)十进制模乘运算☉
十进制模乘运算记为☉。相乘运算后模比100000000大的素数,本文采用模100000007乘法。
(3)十进制数异或运算⊕
十进制数异或运算记为⊕。A⊕B即B按A的相应位变化,若B的相应位是奇数则A相应位作加5运算,若B的相应位为偶数,则A相应位作加0运算,即:
C=A⊕B<=>C[i]=(A[i]+B[i]*5)%10
2、算法的轮变换
基于IDEA加密算法的十进制短分组加密算法首先进行8轮相似的迭代变换,迭代变换过程如图所示。
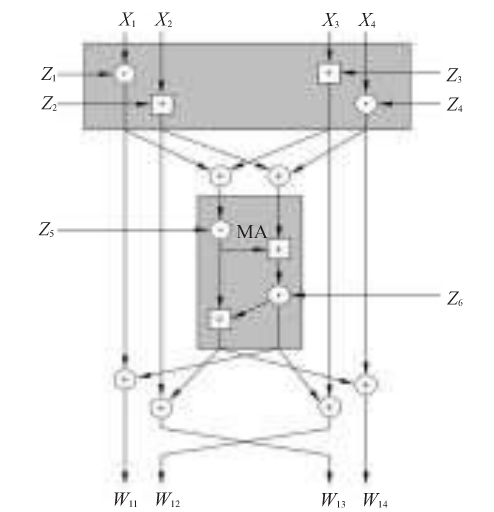
3、密钥扩展算法
借鉴了IDEA的密钥扩展流程,解密子密钥与加密子密钥的关系与IDEA一致。由64位原始密钥生成52个8位子密钥,前八轮每轮使用6个子密钥,输出变换的第九轮使用4个子密钥。64位加密密钥被分为8个8位子密钥(前8个子密钥分别记作Z1,Z2,…,Z8)。然后密钥被左移12位,并再次划分为8个子密钥,下一轮左移13位也划分为8个子密钥。上述两个左移方式交替进行,重复这一过程,直到生成所有的52个子密钥。同IDEA一样,解密子密钥与加密子密钥之间的关系如下表所示:

4、算法的加密和解密
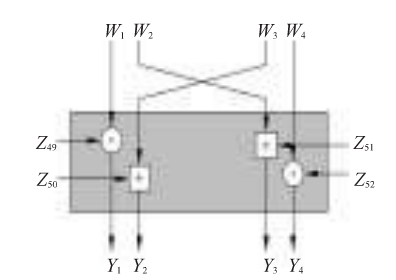
基于IDEA的十进制加密算法的加密流程由上述三种运算构成,进行8轮迭代,最后进行末轮输出变换。整个加密算法的具体加密流程和解密流程如下图所示:

在上图中,左边是加密流程,右边是解密流程。在对IDEA中的运算进行重新定义后,必须保证加密运算与解密运算的可逆性。本文加密算法满足这一性质,下面给出理论证明。现在从下往上考虑。对加密过程的最后一个输出变换,以下关系成立:
Y1=W81☉Z49Y2=W83+Z50Y3=W82+Z51Y4=W84☉Z52
解密过程中第1轮的第1步产生以下关系:
J11=Y1☉U1J12=Y2+U2J13=Y3+U3J14=Y4☉U4
将解密子密钥由加密子密钥表达并将Y1,Y2,Y3,Y4代入以下关系,有:
J11=Y1☉Z49-1=W81☉Z49☉Z49-1=W81
J12=Y2+-Z50=W83+Z50+-Z50=W83
J13=Y3+-Z51=W82+Z51+-Z51=W82
J14=Y4☉Z52-1=W84☉Z52☉Z52-1=W84
可见解密过程第1轮第1步的输出等于加密过程最后一步输入中第2个子段和第3个子段交换后的值。可得以下关系:
W81=I81☉MAR(I81☉I83,I82☉I84)
W82=I83☉MAR(I81☉I83,I82☉I84)
W83=I82⊕MAL(I81⊕I83,I82⊕I84)
W84=I84⊕MAL(I81⊕I83,I82⊕I84)
其中,MAR(X,Y)是MA结构输入为X和Y时的右边输出,MAL(X,Y)是左边输出。则有:
V11=J11⊕MAR(J11⊕J13,J12⊕J14)=W81⊕MAR(W81⊕W82,W83⊕W84)=I81⊕MAR(I81⊕I83,I82⊕I84)⊕MAR[I81⊕MAR(I81⊕I83,I82⊕I84)⊕I83⊕MAR(I81⊕I83,I82⊕I84),I82⊕MAL(I81⊕I83,I82⊕I84)⊕I84⊕MAL(I81⊕I83,I82⊕I84)]=I81⊕MAR(I81⊕I83,I82⊕I84)⊕MAR(I81⊕I83,I82⊕I84)=I81
同理,可有V12=I83,V13=I82,V14=I84。
所以解密过程第1轮第2步的输出等于加密过程倒数第2步输入中第2个子段和第3个子段交换后的值。
同理可证上图中每步都有上述类似关系,这种关系一直保持到V81=I11,V82=I13,V83=I12,V84=I14。即除第2个子段和第3个子段交换位置外,解密过程的输出变换与加密过程第1轮第1步的变换完全相同。
综上可知,整个解密过程的输出等于整个加密过程的输入。
二、基于IDEA加密算法的十进制短分组加密算法性能分析
定义1:对于加密函数EK(P)中的参数K和P(解密函数DK(C)中的参数K和C),每次加(解)密只改变其中某个参数的一位,另一个参数保持不变,把多次加(解)密得到的密(明)文相比较,每一位上相异的比率称为加密(解密)扩散率[2]。
由定义1可知,扩散率越大,相同的明文不同的密钥加密得到相同的密文的概率就越小,可以更有效的防止攻击者已知部分密钥相关性攻击。扩散率越大,密码的雪崩效应越好,安全性也就越高。
定义2对于一个加密算法,若扩散率大于等于0.5,则称该加密算法达到了完全扩散。我们对该算法的加密性能进行了软件仿真测试分析。分别以8位、16位、32位、64位十进制数为加密分组,进行1到8轮的加密、解密运算测试。下面是以32位十进制数为加密分组所得的测试结果。加密过程中明文对密文的扩散率,密钥对密文的扩散率如图所示:
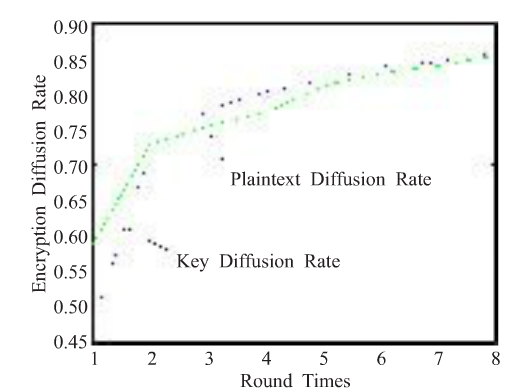
解密过程中密文对明文的扩散率,密钥对明文的扩散率如图所示。
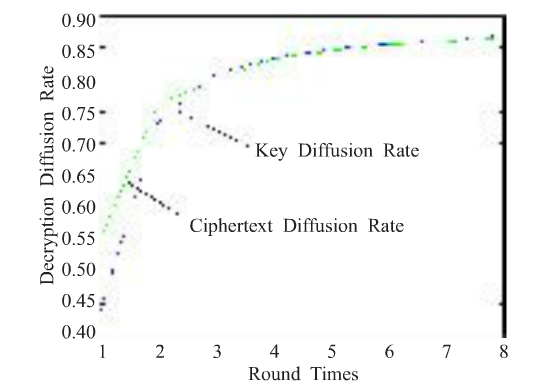
从图中可看出,第1轮加密的输出就已经有了很好的扩散性,2轮加密过后所有扩散率均达到了完全扩散。
此加密算法借鉴了IDEA密码的思想,并对其中的运算进行了重新定义,以适应十进制数加密、解密的要求。引入的新的十进制运算能够很好地完成对十进制分组的加密和解密,并对加密与解密的可逆性进行了理论证明。算法实现容易,加密解密速度快,加密强度高,具有较高的安全性,该加密算法可广泛用于各种需要十进制数加密的领域。
小知识之IDEA加密算法:
IDEA(International Data Encryption Algorithm)是瑞士的James Massey,Xuejia Lai等人提出的加密算法,在密码学中属于数据块加密算法(Block Cipher)类。IDEA使用长度为128bit的密钥,数据块大小为64bit。从理论上讲,IDEA属于“强”加密算法,至今还没有出现对该算法的有效攻击算法。










