目前图像加密技术主要有象素位置置乱加密技术和象素灰度值加密技术两大类方法。象素位置置乱加密技术的运算量比较大,要求对图像的所有象素点遍历一次,同时还要考虑地址之间的相关性。象素灰度值加密技术易实现、运算量小、效果较好。那么我们今天就运用象素灰度值加密原理,来实现了基于二维Logistic混沌映射的数字图像象素灰度值加密算法。
一、二维Logistic混沌映射系统
Logistic映射系统简单实用,其一维形式研究使用的较多,但一维Logistic映射生成的混沌序列经过简单地变换加密是一种平凡混沌加密系统,安全性难以保障。我们可利用二维Logistic映射,选择不同的参数,产生二维的混沌点集合。适当地将其离散化用于加密过程,此时的加密算法是二维化的。可以证明二维映射混沌点集不存在有效的无误差构造形式,具有更为安全的加密效果。
1、二维 Logistic映射定义
根据一维Logistic映射,定义二维Logistic映射为:
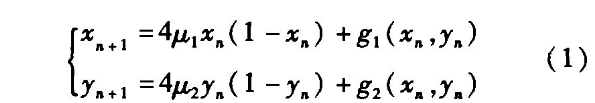
其中g1和g2是耦合项,可取两种情况:
①g1=γyn和g2=γxn的一次耦合项;
②g1=g2=γxnyn的对称二次耦合项。
采用具有一次耦合项形式的二维Logistic 映射进行研究实现,映射形式为:
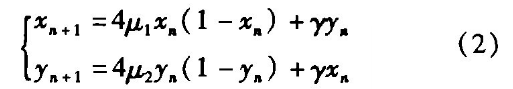
其动力学行为是由控制参数μ1、μ2和γ决定,可有选择地研究控制参数沿参数空间中的轨线变化时系统行为的演化。
2、二维Logistic映射的混沌
非线性动力学系统的混沌具有不可预测性、不可分解性和具有规律性行为等特性,混沌定义为:设(x,ρ)是一紧致的度量空间,f:X→X是连续映射,称f在X上是混沌的,如果:
①f具有对初值敏感依赖性;
②f在X上拓扑传递;
③f的周期点在X中稠密。
非线性系统随时问的演变将趋向于维数比原来相空间低的极限集合,即吸引子。随着控制参数的变化,简单吸引子发展为奇怪吸引子,此时系统是混沌的。研究混沌运动,可直接观察分岔图和相图。
当μ1=μ2=μ∈[0.6,0.9],γ=0.1,初始点(X0,Y0)=(0.10,0.11)时,下图是具有一次耦合项的二维 Logistic映射的分岔图。从图中可看出μ<0.815时,系统为周期运动,0.815<μ<0.89时,大部分情况对应为混沌运动,但有几处很窄处为混沌区中的不同周期的周期窗口,μ≥0.89时,系统为混沌。

选择控制参数为μ1=μ2=μ=0.89,γ=0.1,初始点为(X0,Y0)=(0.10,0.11)时,其相图为:
 为具有一次耦合项的二维Logistic映射的奇怪吸引子。
为具有一次耦合项的二维Logistic映射的奇怪吸引子。
观察相图可见,整体上系统是稳定的,局部是不稳定的,相邻运动轨道互相排斥而按指数分离,奇怪吸引子具有无穷层次的自相似结构并且其运动依赖于初始条件。根据以上分析,具有一次耦合项的二维Logistic映射系统满足混沌运动和混沌加密的要求。
二、数字图像的二维混沌加密算法
选择控制参数μ1=μ2=μ=0.9,γ=0.1,初始(X0,Y0)=(0.10,0.11)时,用具有一次耦合项的二维Logistic混沌映射序列迭代值,对数字图像灰度值进行象素加密。加密算法描述如下,解密算法是加密算法的逆过程。
1、 将原始大小为w×h的灰度值图像矩阵转换为一维,存储于大小wh的一维数组 image[]中。在image[]中,每个元素值的取值范围都在0~255之间,并将image[]中的值全部转换为8位二进制数存储在大小为8的一维数组image2[]中。
2、利用二维 Logistic函数产生(wh+100)对值为0~1的混沌序列值。舍去前100对值,取第101~第(wh+100)的共wh对值,并分别存储于数组x[]与y[]中。
3、将x[]与y[]中的值分别乘以16后取整,得到一系列值为0~16的序列值,并全部转换为4位二进制,存储在大小分别为4的一维数组 x2[]和y2[]中。
4、利用x2[]和y2[]分别与image2[]的有关各位进行异或运算,得到加密序列值,存于大小为8的一维数组changed[]中。
5、_将changed[]中的8位二进制转换为0~255的灰度值,然后转换成二维矩阵,得到加密后的图像。
基于混沌的图像加密技术是近年来才发展起来的一种密码加密技术,是把待加密的图像信息看成是按照某种编码方式的二进制的数据流,利用混沌信号来对图像数据流进行加密的。混沌之所以适合于图像文件加密,这是与它自身的有些动力学特点密切相关的。二维Logistic混沌映射系统产生的序列对数字图像象素的灰度值进行奇偶异或运算加密,得到了较好的加密效果,其安全性和计算性能合适,具有一定的实用价值。
小知识之非线性动力学
随着科学技术的发展,非线性问题出现在许多学科之中,传统的线性化方法已不能满足解决非线性问题的要求,非线性动力学也就由此产生。











