加密算法中的Feistel结构是什么意思?
在对称加密算法中,我们经常可以看到某个算法采用Feistel结构设计,如DES算法、Blowfish算法等。那么这个“Feistel”结构是什么意思呢?它对算法有哪些影响呢?下面我们就来了解一下。
Feistel结构的介绍
在密码学中,Feistel结构是一种常见且经典的分组密码设计模式,由密码学家Horst Feistel于1973年首次提出。它是一种特定的横向拆分算法,用于将原始输入的纵向分解和拆分成若干横向分割的段,其中每一段都是一个独立的函数。
Feistel密码的核心是代替和置换,代换是指每个明文元素或元素被唯一地替换为相应的密文元素或元素组,置换是指将明文元素的序列被替换为该序列的一个置换。

Feistel结构的原理
Feistel结构通过将明文分组分成左右两半部分,左半部分采用替换操作,右半部分采用基于子密钥的轮函数(包括替换和置换组合操作)进行混淆,经过n轮迭代处理后再重新合并组成密文分组。具体步骤如下:
- 将明文数据分为左半部分(L)和右半部分(R),L₀和R₀是初始明文分块。
- 使用相同的变换函数(F)对右半部分进行处理,通常使用轮密钥(round key)与之结合。
- 将处理后的结果与左半部分做异或操作,得到新的右半部分(R₁)。
- 将上一轮的右半部分(R₁)作为新的左半部分(L₁),并重复应用相同操作。
- 经过多轮迭代后,最终得到加密后的密文。
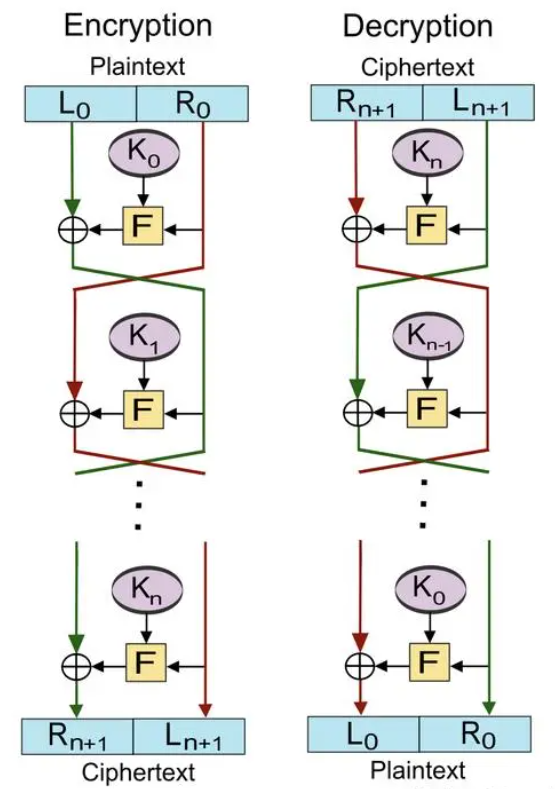
Feistel结构的解密过程与加密过程类似,只是轮密钥的应用是相反的顺序。通过应用相同的变换函数和相反顺序的轮密钥,可以完成解密操作。
Feistel结构的优势
- 安全性:Feistel结构通过多轮的迭代运算和轮密钥的应用,增加密码算法的安全性。即使变换函数本身相对简单,多轮迭代可以增加密码的复杂性,提高对抗攻击的能力。
- 可逆性:Feistel结构的加密和解密操作是可逆的,通过应用相反的轮密钥和变换函数,可以恢复原始明文。
- 并行性:在Feistel结构中,每个轮操作只涉及到左右两个部分进行计算,这使得并行计算成为可能,从而提高了加密和解密速度。

Feistel结构的重要性
- 安全性与可靠性:Feistel结构通过迭代运算和轮密钥的应用,为分组密码算法提供了坚实的安全基础。它允许密码算法在经过多轮迭代后变得更加安全可靠。
- 快速且高效:Feistel结构的并行性质使得密码算法能够在硬件和软件上进行高效实现。它允许多个分块同时进行处理,从而提高了加密和解密的速度。
- 灵活性和扩展性:Feistel结构可以适应不同长度的密钥和分组大小,并支持不同的变换函数。这使得密码算法可以根据需要进行调整和扩展,以适应不同的应用场景。
- 可逆性和完整性:Feistel结构的加密和解密过程是可逆的,能够确保加密数据的完整性和可信性。通过应用相反的轮密钥和变换函数,可以完全恢复原始明文。
免责声明:素材源于网络,如有侵权,请联系删稿。
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。




