随着互联网的发展和云计算概念的诞生,传统的加密手段显然无法满足人们日益增长的加密需求。于是,同态加密开始出现在人们的视野当中。下面我们就一起来了解一下同态加密技术。
同态加密技术简介
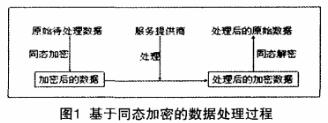
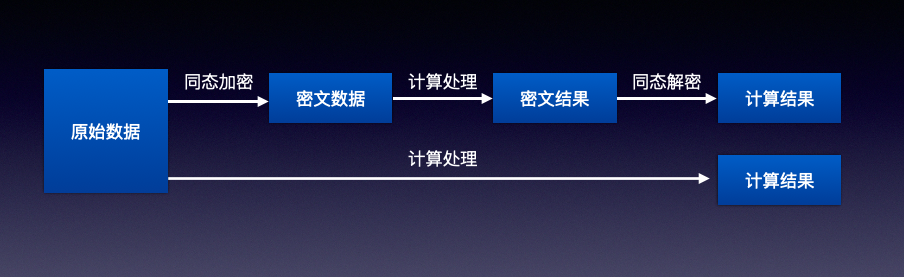
同态加密(HE,homomorphic encryption)是密码学里一种特殊的加密模式,同态加密使我们可以将加密后的密文发给任意的第三方进行计算,并且在计算前不需要解密,即可以在密文上进行计算。
虽然同态加密的概念最早出现于20世纪70年代,但是第一个支持在密文上进行任意运算的全同态加密框架出现较晚,在2009年由IBM的研究人员Craig Gentry提出。

同态加密技术的原理
同态加密技术,就是将数据加密成难以破译的数字字符串,能对这些加密后的字符串进行数学处理,然后解密结果。如果用数学方法表述,假设加密操作为E,明文为m,加密得e,即e=E(m),m=E'(e)。已知针对明文有操作f,针对E可构造F,使得F(e)=E(f(m)),这样E就是一个针对f的同态加密算法。
我们举一个简单的例子,看看同态加密是如何处理2+3这样的问题:
假设数据已经在本地被加密了,2加密后变为22,3加密后变为33。加密后的数据被发送到服务器,再进行相加运算。然后服务器将加密后的结果55发送回来。然后本地解密为5。
同态加密技术的分类
部分同态加密
部分同态加密(Partial HE,简称PHE)指同态加密算法只对加法或乘法(其中一种)有同态的性质。 例如RSA加密是最早应用的公钥加密算法框架,同时RSA算法也是一种PHE算法,其对乘法有同态的性质。PHE的研究成果出现比较早,并且加法同态加密算法(Additive HE)比乘法同态加密算法要多一些。
PHE的优点是原理简单、易实现,缺点是仅支持一种运算(加法或乘法)。
层次同态加密算法
层次同态加密算法(LHE,Leveled HE或SWHE,SomeWhat HE)一般支持有限次数的加法和乘法运算。 层次同态加密的研究主要分为两个阶段,第一个阶段是在2009年Gentry提出第一个FHE框架以前,比较著名的例子有BGN 算法、姚氏混淆电路等;第二个阶段在Gentry FHE框架之后,主要针对FHE效率低的问题。
LHE的优点是同时支持加法和乘法,并且因为出现时间比PHE晚,所以技术更加成熟、一般效率比FHE要高很多、和PHE效率接近或高于PHE,缺点是支持的计算次数有限。

全同态加密算法
全同态加密算法(Fully HE,简称FHE)支持在密文上进行无限次数的、任意类型的计算。从使用的技术上分,FHE的类别有基于理想格的FHE方案、基于LWE/RLWE的FHE方案等等。
FHE的优点是支持的算子多并且运算次数没有限制,缺点是效率很低,目前还无法支撑大规模的计算。
由于同态加密技术在计算复杂性、通信复杂性与安全性上的优势,更多的研究力量投入到其理论和应用的探索中,这将使得同态加密技术越来越向实用化靠近。
免责声明:素材源于网络,如有侵权,请联系删稿。