基于混沌力学体制的图像加密技术中,通常使用一维的Logistic映射,二维的smale映射和Henon映射,以及三维的Lorenz系统。针对制造企业信息化系统安全建设的需要,有专家们提出了基于Logistic映射的双Logistic映射复合混沌系统,由两套Logistic映射组合起来构成。每套Logistic映射都能够通过自己产生的实数混沌序列,在某种有效策略的控制下来扰动另一套映射的参数。充分利用Logistic映射对参数敏感的特点,使得生成的实数混沌序列具有更大的随机性,以加强对图像的加密效果,保证图像信息的高安全性。
一、双Logistic映射复合混沌系统算法分析
1、混沌的定义及Logistic映射
混沌现象是在非线性动力系统中出现的确定性的、类似随机的过程,这种过程既非周期又不收敛,对初始值有极其敏感的依赖性,关且具有白噪声的统计特性。通过混沌系统对初始值和结构参数的敏感依赖性,可以提供数量众多、非相关、类随机而又确定可再生的混沌序列。由于上述特点,混沌可以广泛应用于加密。
最基本的混沌模型是“虫口模型”,即Logistic映射:
xn+1=μxn(1-xn) _ _ (1)
其中x为映射变量,μ为系统参数,它们的取值范围分别为:0≤xn≤1,1<μ≤4。Logistic映射是一个非常简单,却又具有重要意义的非线性迭代方程,它具有确定的形式,并且系统不包含任何随机因素,但系统却能产生看似完全随机的、对参量μ的动态变化和初值极为敏感的现象。选定μ=3.9有:
Xn+1=4xn(1-xn),x∈(n,1) _ (2)
下表证明了Logistic映射对初始值的敏感性。
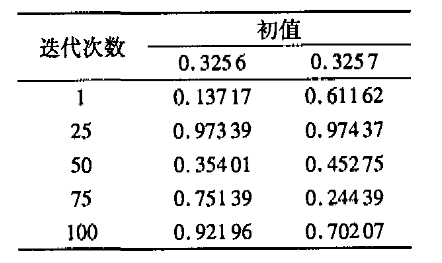
由于混沌序列随机的确定性,SehusterH.G证明混沌序列(1)的概率分布密度函数为:
 (3)
(3)
可见,p(x)不依赖初始值,它的遍历性等同与零均值白噪声,同时它还具有8-like型自相关函数和零的互相关函数。作为一种非线性序列,该序列结构复杂难以分析和预测,因此可以用混沌系统迭代产生的混沌序列进行加密。
2、参数变化的双Logistic映射复合混沌系统
混沌系统不仅对初始条件敏感,而且对混沌参数也非常敏感。为了增强Logistic映射产生的混沌序列的随机性,将两套Logistic映射系统组合起来,相互控制对方的参数来进行扰动,从而在产生混沌序列的过程中充分利用混沌系统对混沌参数敏感的特性:
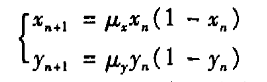 (4)
(4)
为了达到(4)中两个方程式相互控制对方的参数μ从而进行扰动,需要给μx和μy分别设置取值范围,为此需要引入参数切换控制条件来控制各Logistic映射的参数在不同的值之间进行切换。
可以给离散数值解x序列和y序列各设置一个阈值,Uxsign和Uysign,然后使离散值和阈值进行比较,根据比较结果来切换参数的取值。按照以下方式来决定Uxsign和Yysign的取值:
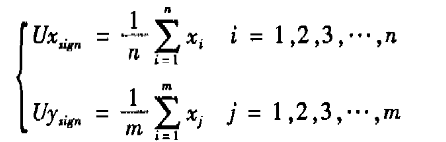 (5)
(5)
公式(4)Logistic映射的参数切换定义如下:

(6)
因为Logistic映射序列中,各离散值的平均值接近0.5,为了简单,试验中Uxsign和Uysign的取值固定为0.5。该系统中的每个Logistic映射子系统通过自身的输出状态变化来改变另外一个Logistic映射子系统的参数,实现子系统之间的相互作用,从而构成参数变化的双Logistic映射复合混沌系统。该系统基于Logistic映射对初值敏感,也对参数非常敏感的基础之上,产生的混沌序列不但继承了单一Logistic映射混沌序列的特点,相比之下序列的随机特性更强,所以本算法产生的序列能够用来给图像文件加密。
二、基于复合混沌系统的图像加密模型与算法
1、混沌系统用于图像加密的基本设计思想
由于混沌系统具有遍历性、混合性和指数发散性,完全符合密码学的要求;更因为混沌在二维平面上的不规则性,使得混沌系统更加适合于图像数据的加密。混沌系统用于图像加密的基本设计思想通常有以下几种:
(1)将加密系统的密钥设置为混沌系统的初始值(或者系统参数),之后经过密码学中类似于Felstel网络的多次迭代来实现对明文和密钥的充分混合和扩散;
(2)将混沌系统作为伪随机序列发生器,其中混沌系统由离散混沌系统或经过离散化的连续混沌系统构成;这种由混沌系统产生的伪随机序列于明文进行异或操作,所得输出即为密文;
(3)基于二维混沌的分组密码加密体制,通过映射对明文进行置换操作,再应用某种简单的替代操作,经过多轮(小于15轮)迭代来实现对数据文件的有效加密。
2、算法的设计
要加密尺寸为n=M×N的图像,,首先给出密钥key,采用某种策略生成公式(4)中两个方程式的初始值X0和Y0。为了试验简单,这里采用策略X0=key×0.6和Y0=key×0.3,并且系统中给参数μy和μx已经赋有能生成混沌序列的默认值。随后,利用“参数变化的双Logistic组合混沌系统”算法生成实数混沌序列Xn和Yn。
(1)利用实数混沌序列生成置乱矩阵(置乱模板)及图像的置乱
前面描述过,尺寸为n=M×N的图像,可以看作是平面区域上的二元连续函数,在图像数字化之后,1=F(X,Y)则对应于一个矩阵,现在对矩阵的元素按从左到右、从上到下的次 序依次编号1-n,如此以来就为原图取了一个固定模板Q。
现在,根据实数混沌序列来做一个与原图模板Q大小相同的置乱模板(置换矩阵)P。因为原图模板Q中像素编号最大为n,这就要求置乱模板P中的编号也必须在[O,n]内。
(2)利用实数混沌序列Yn生成灰度变换矩阵G及通过异或运算加密
通常而言,由Logistic映射生成混沌序列有实数值序列、二值序列、位序列和四值混沌序列等四种方法。其中较常用的是二值序列方式,该方式虽然在一定程度上降低了序列的随机性,但是实现简单,效率高;并且,我们在前面设置参数的切换条件时也用到相同算法。所以在生成灰度变换矩阵时仍然采用二值序列。利用另外一个实数混沌序列Yn,首设置阈值Uxsign。
(3)解密算法实现
输入正确的密钥,将加密算法逆向运算,就能对加密后的图像解密,恢复为原图像。
基于复合混沌系统的数字图像加密方法适用于企业产品图像信息在网络环境下的安全传输,有利于加强企业信息资源的安全。
小知识之混沌力学体制:
混沌动力学是复杂性科学的一个重要分支,也是近三十年来的一个热门学科。混沌(Chaos)是指发生在确定性系统中的貌似随机的不规则运动。一个确定性理论描述的系统,其行为却表现为不确定性、不可重复、不可预测,这就是混沌现象。混沌是非线性系统的固有特性,是非线性系统普遍存在的现象,牛顿确定性理论能够处理的多为线性系统,而线性系统大都由非线性系统简化而来。因此,在现实生活和实际工程技术问题中,混沌是无处不在的。










