admin CORDIC加密算法是一种用于计算一些常用的基本运算函数和算术操作的循环迭代加密算法。其基本思想是用一系列与运算基数相关的角度的不断偏摆来逼近所需旋转的角度,从广义上讲它是一个数值型计算逼近的方法。由于这些固定的角度与计算基数有关，运算只有移位和加/减。若用传统的乘、除等计算方法，需要占用大量的硬件资源，甚至算法是难以实现的，这样就不能满足设计者的要求。
一、CORDIC加密算法原理
CORDIC加密算法主要用于计算三角函数、双曲函数、指数和对运算，其基本思想是通过一系列因定的与运算基数相关的角度断偏摆来逼近所需的旋转焦度，使得矢量旋转和定向运算不需三角函数查表及乘、开方、反三角函数等复杂的数学运算，原理如图所示。
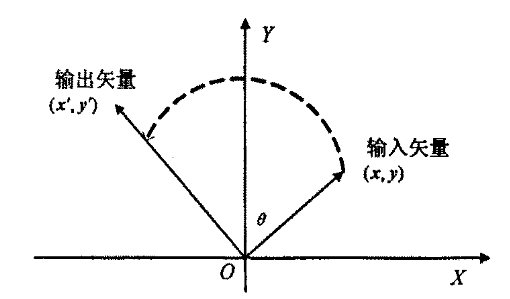对矢量（x,y）旋转θ角度成（x’,y’），则有
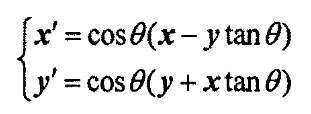
上式中，旋转角度θ满足tanθ＝±2'时，tanθ乘法运算键纯为简单的移位运算。通过连续进行一系列的基本角度单元旋转，可实现任意角度的旋转。上式可表示为：
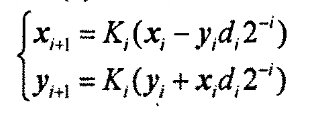
公式中
CORDIC加密算法一般工作在旋转和矢量两种模式下。旋转式为将矢量旋转一个给定的角度；矢量模式为将输入矢量旋转X轴，同时记录下旋转的角度。
二、CORDIC加密算法典型应用
1、arctan的计算
如果角度累加器初始化为0，反正切值θ＝arctan（y／x）可使用矢量模式下的CORDIC旋转直接得到。
2、矢量幅值的计算
在矢量模式下，CORDIC旋转器对输入矢量计算反正切值得到的副产品是矢量幅值，矢量旋转后，矢量被调整到x轴上，其幅值正好是该矢量的x分量：
３、对数运算
根据对数和反双曲余切函数的线性关系，以10为底的对数可以通过计算反双曲余切函数得到：
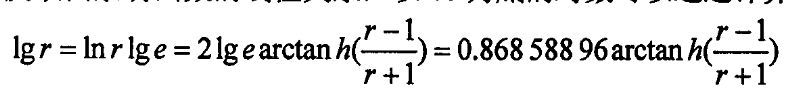
CORDIC加密算法将输入矢量（x,y），沿着双曲线旋转到（x’，0），如图所示。
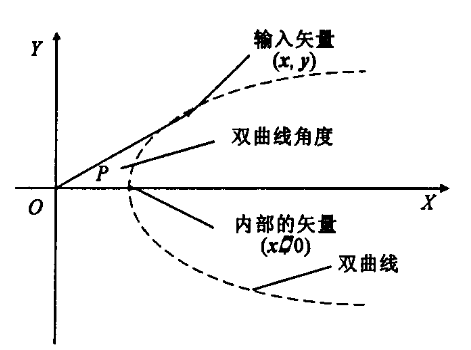
计算的结果是双曲线角度，arctanh（y／x）。双曲线角度代表了输入矢量（x,y）覆盖的对数面积。
CORDIC加密算法应用范围相当的广泛，譬如用于计算机制图中求点到线的距离浏、直角坐标与极坐标的相互变换及求多维矢量的欧几里德范数等，可以预见，随着VLSL技术的发展以及对速度、精度要求的越来越高，CORDIC加密算法将得到越来越广泛的应用。
小知识之双曲函数：
在数学中，双曲函数类似于常见的（也叫圆函数的）三角函数。基本双曲函数是双曲正弦“sinh”，双曲余弦“cosh”，从它们导出双曲正切“tanh”等。也类似于三角函数的推导。反函数是反双曲正弦“arsinh”（也叫做“arcsinh”或“asinh”）以次类推。
