同态加密是一种独特的加密形式,它允许用户在加密情况下对数据执行计算,而无需先进行解密。而在同态加密的基础上,还有一种名为“全同态加密”的方法,这是什么意思呢?我们今天就来简单了解一下。
全同态加密简介
全同态加密英文名为Fully Homomorphic Encryption,简称FHE,是支持对密文进行任意计算的密码系统。这种方案能够为任何所需功能构建程序,这些功能可以在加密输入上运行以产生结果加密。由于这样的程序永远不需要解密其输入,因此它可以由不受信任的一方运行,而不会泄露其输入和内部状态。

全同态加密举例
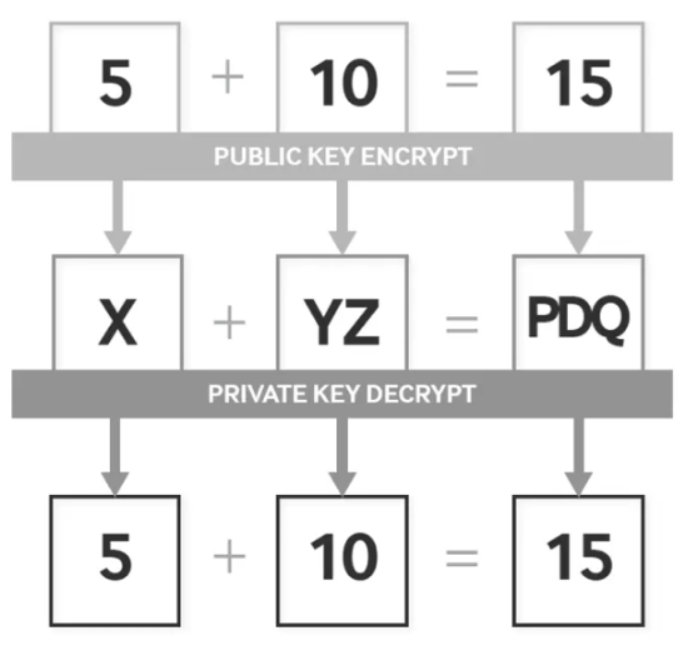
在全同态加密中,我们将5和10可以分别加密为X和YZ,X+YZ的计算结果为PDQ,而PDQ解密后的结果为15,与加密前的计算结果5+10=15完全相同。其中,X+YZ=PDQ被称为密文计算,在密文计算的过程中,随时可以被解密。
全同态加密的应用
全同态加密技术是一种趋势性技术,它可被应用于外包计算、隐私保护机器学习、安全多方计算、联合学习、数据交换和共享等领域。大量的专家和学者对其进行了研究,目前,同态加密技术的研究主要集中在提高计算速度、缩短密文长度、扩展数据类型、扩大支持操作等方面。
全同态加密的优势
基于全同态加密的特性,它可被用于保护隐私的外包存储和计算以及在加密的数据中进行诸如检索、比较等操作,得出正确的结果,而在整个处理过程中无需对数据进行解密。
它的意义在于,能够解决将数据及其计算委托给第三方时的数据安全问题。对于医疗保健信息等敏感数据,全同态加密可用于通过消除抑制数据共享产生的隐私安全问题或提高现有服务的安全性来启用扩展新的服务。
例如,由于医疗数据隐私问题,医疗保健中的预测分析可能难以通过第三方服务提供商处理,如果预测分析服务提供商可以对加密数据进行操作,就会减少因为使用第三方服务而产生的隐私安全问题。即使服务提供商的系统受到安全威胁,数据也将保持安全。

全同态加密的不足
目前已知的全同态加密算法需要消耗大量计算资源的计算时间,还达不到实用的标准。且由于全同态加密算法只支持加法和乘法同态,很多数理统计方法,会有开根号等计算,还需要使用到信息论和数学中的逼近理论,通过近似算法来达到相同或相近的计算目的,这类计算通常也会伴随着精度丢失、误差偏大等问题。
免责声明:素材源于网络,如有侵权,请联系删稿。







