ID3加密算法在绩效评估中的应用
绩效分析评估的任务是根据评估的目的、标准和方法,对所收集的数据进行分析、处理、综合。等级评价法是一种较为常用的分析评估方法。这种方法具有简单、容易操作等优点,但在绩效反馈方面存在重大缺陷。虽然这种缺陷可以通过面谈的方式解决,但太耗费人力、物力和财力。为了节约绩效管理成本,提高绩效反馈效率和企业绩效,我们在等级评价法的基础上引入决策树方法中的ID3加密算法。
一、ID3加密算法基本原理
ID3加密算法起源于概念学习系统,是迄今为止在国际上最早有影响力的决策树方法。其基本原理是采用分治策略,通过对一个训练集进行学习生成一棵决策树。在决策树生成过程中,通常使用信息增益方法来帮助确定生成每个结点时所应选择的合适属性,进而选择具有最高信息增益(熵减少的程度最大)的属性作为当前结点的测试属性,以便对之后划分获得的训练样本子集进行分类所需要的信息最少。也就是说,利用该属性对当前结点所含样本集合进行划分,能使所产生的各样本子集中的“不同类别子例混合程度”降为最低,有效减少划分次数。决策树是用样本的属性作为结点,用属性的取值作为分支的树结构。决策树的根结点是所有样本中信息量最大的属性,中间结点是以该结点为根的子树所包含的样本子集中信息量最大的属性,叶结点是样本的类别值。
采用ID3加密算法的基本操作方法是,首先,找出最具判别力(信息增益)的属性,将数据分成多个子集。然后,找出每个子集最具判别力的属性,再进行数据划分,直到所有子集仅包含同一类型的数据为止。这样,就得到一棵决策树,可以用来对新的实例进行分类。ID3加密算法可分为主算法和建树算法两种。
1、ID3主算法。
主算法流程如图所示。其中,PE、NE分别表示正例和反例集,它们共同组成训练集。PE'、PE''和NE'、NE''分别表示正例集和反例集的子集。
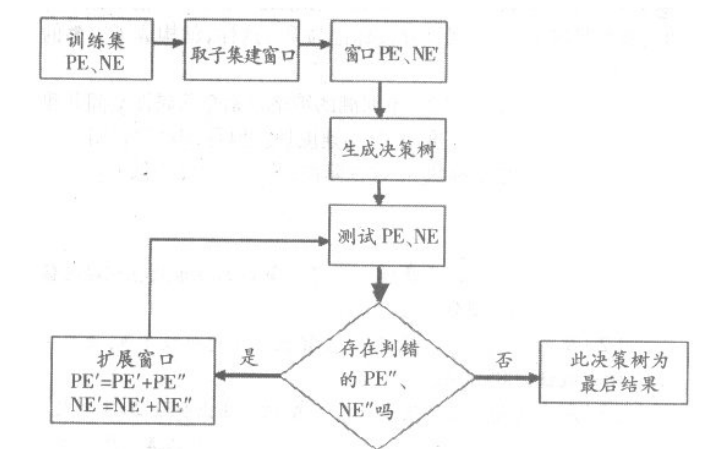
2、建树算法。
采用建树算法建立决策树,首先,对当前子例进行同类归集。其次,计算各集合属性的互信息,选择互信息最大的属性Ak。再次,将在Ak处取值相同的子例归于同一子集,Ak取几个值就几个子集。最后,对既含正例又含反例的子集递归调用建树算法。若子集仅含正例或反例,对应分支标上P或N,返回调用处。
二、ID3加密算法在绩效评价中的应用
我们以某销售公司的业务员绩效考核为例,运用决策树的ID3加密算法对业务员进行绩效评价,业务员的绩效考核指标及指标考核结果如表所示。
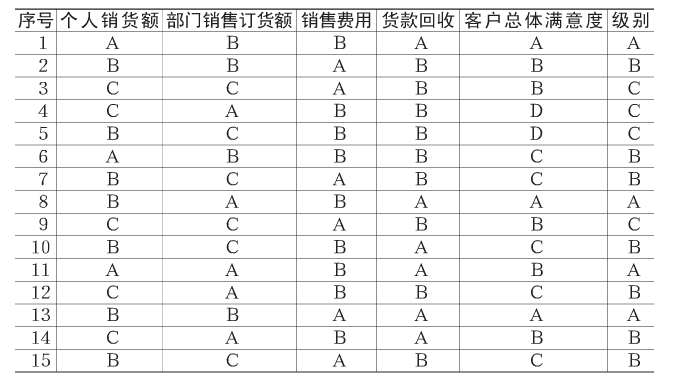
1、计算信息熵
15个业务员的级别被分为A、B、C三种,其中有4个A级,7个B级和4个C级。则P(u1)=4/15,P(u2)=7/15,P(u3)=4/15,
信息熵H(U)=4/15log2(15/4)+7/15log2(15/7)+415log2(15/4)=1.53bit。
2、计算条件熵
分别就上班中的项目计算条件熵:
(1)个人销售货额V1
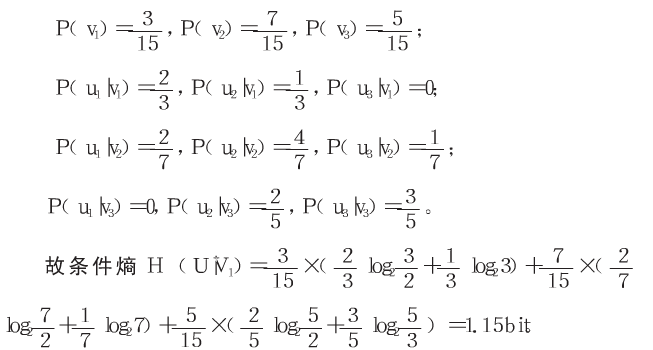
(2)部门销售订货额V2

(3)销售费用V3
(4)货款回收V4
(5)客户总体满意度V5
3、计算互信息
根据以上计算结果求五个特征的互信息,也就是信息熵增益。
由计算结果可知,客户总体满意度的互信息值最大。故客户总体满意度为决策树的第一根节点。
4、建决策树的树根和分枝
互信息计算结果表明,应选择互信息最大的特征客户总体满意度作为树根。对客户总体满意度的4个取值进行分枝,对应的4个子集分别是:F1={1,8,13};F2={2,3,9,11,14};F3={6,7,10,12,15};F4={4,5}。其中,F1中的实例均属A类,对应分枝标记为A;同理,F3对应分枝标记为B,F4对应分枝标记为C;F2中包含A、B和C三类,应递归调用建树算法。
5、递归建树
对子集F2运用ID3加密算法对5个特征求互信息。
首先,计算子集F2的信息熵。
从计算结果可知,部门销售订货额的互信息最大,故应以部门销售订货额作为该分枝的根节点,再向下分枝。
当部门销售订货额取B时,业务员级别全为B类,则该分枝标记为B;当部门销售订货额取取C时,业务员级别全为C类,则该分枝标记为C。当部门销售订货额为A时,该子集{11,14}对应业务员级别有A和B两类。同理,递归调用ID3加密算法可求出个人销货额的互信息最大,故以个人销货额作为根节点,向下分枝。当个人销货额取A时,业务员级别为A,则该分枝标记为A;当个人销货额取C时,业务员级别为C,则该分枝标记为B。这样,就构成了完整的决策树。
ID3加密算法采用自顶向下不回溯的策略搜索全部属性空间并建立决策树,算法简单、深度小、分类速度快。但是,ID3加密算法对于大的属性集执行效率下降快、准确性降低,并且学习能力低下。
小知识之ID3加密算法
ID3加密算法作为一个贪心算法是采用自顶向下的贪婪搜索的方法对所有可能的决策空间进行遍历,对以前的选择从不回溯重新考虑,并采用自上而下、分而治之的策略对决策树分支递归扩展并最终完成决策树的构建。











