简述RSA加密算法
之前的文章中我们聊了聊AES加密算法,今天我们来聊聊另一种历史悠久且应用广泛的算法——RSA。
它是1977年由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)共同提出的一种加密算法,RSA就是他们三人姓氏开头字母拼在一起组成的。

RSA算法是一种非对称加密算法,这一算法主要依靠分解大素数的复杂性来实现其安全性,由于大素数之积难被分解,因此该密码就难被破解。
几十年来,RSA算法经历了各种攻击的挑战,根据相关显示,目前被破解的最长RSA密钥是768个二进制位。也就是说,长度超过768位的密钥,还未被破解,至少目前尚未有人公开宣布。
RSA原理
RSA基于一个十分简单的数论事实:将两个大素数相乘十分容易,但想要对其乘积进行因式分解却极其困难,因此可以将乘积公开作为加密密钥,即公钥,而两个大素数组合成私钥。公钥是可发布的供任何人使用,私钥则为自己所有,供解密之用。
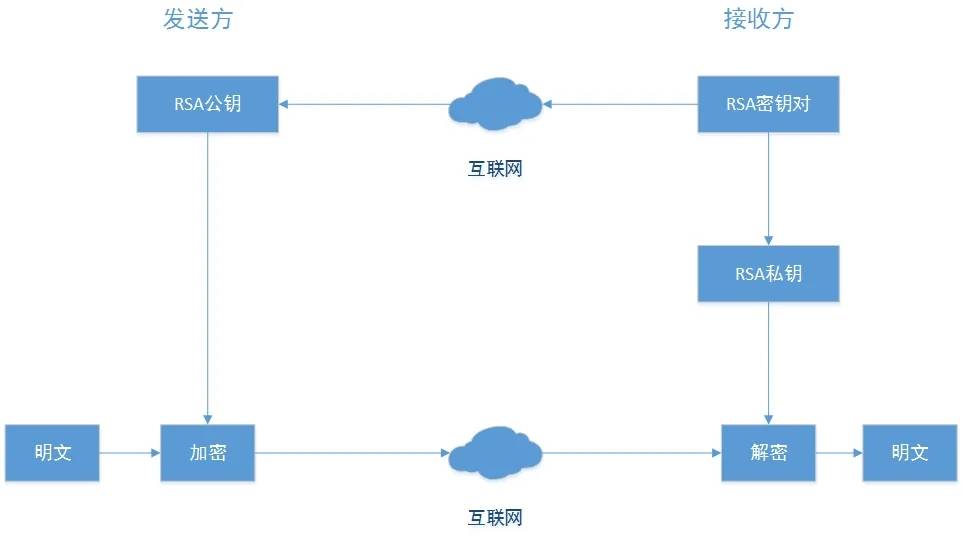
RSA公私钥生成流程
- 随机找两个质数P和Q,P与Q越大,越安全。(例如:61和53)
- 计算p和q的乘积n。(n=61×53=3233,n的长度就是密钥长度。3233写成二进制是110010100001,一共有12位,所以这个密钥就是12位。)
- 计算 n 的欧拉函数φ(n)。(根据公式φ(n)=(p-1)(q-1)算出φ(3233)等于60×52,即3120)
- 随机选择一个整数e,条件是1<e<φ(n),且e与φ(n) 互质。(条件是1<e<φ(n),且e与φ(n) 互质。1到3120之间,随机选择了17。)
- 有一个整数d,可以使得ed 除以φ(n) 的余数为 1。(ed ≡ 1 (mod φ(n)),即17*2753 mode 3120=1)
- 将n和e封装成公钥,n和d封装成私钥。(n=3233,e=17,d=2753,所以公钥就是:3233,17,私钥就是:3233, 2753。)
RSA加密
首先对明文进行比特串分组,使得每个分组对应的十进制数小于n,然后依次对每个分组m做一次加密,所有分组的密文构成的序列就是原始消息的加密结果,即m满足0<=m<n,则加密算法为:c=m^e mod n; c为密文,且0<=c<n。
RSA解密
对于密文0<=c<n,解密算法为:m=c^d mod n。
RSA加密算法的优缺点
优点:RSA算法是国际标准算法,属于主流算法之一,应用广泛,兼容性比较广,能够适用于各种不同的系统之中,不容易出现限制问题。
缺点:RSA算法加密长度为2048位,对于服务器的消耗是比较大的,计算速度也比较慢,效率偏低,一般只适用于处理小量数据。

尽管RSA加密算法运行消耗大,效率低,但是由于其优秀兼容性和安全性,它依旧是使用最广泛的非对称加密算法。
免责声明:素材源于网络,如有侵权,请联系删稿。











