FEAL作为一种快速的加密算法,在安全性要求较低的领域中,有着非常广阔的应用前景。
FEAL加密算法属于对称密钥体制,64位密钥加密64位明文,其加密变换采用交替使用换字、换位,以使在密文中消失明文的痕迹,具体过程可分为初始变换、运用服务函数f的n次重复迭代、逆初始变换3部分。其加密算法如图所示:
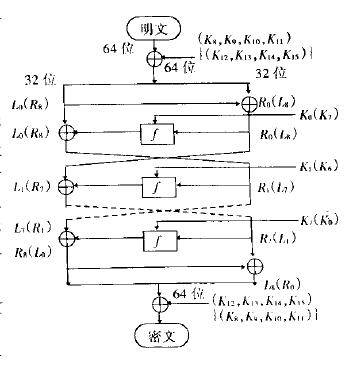
FEAL加密算法流程图
FEAL加密算法过程简述:
一个64位的明文分组后与64位的的密钥相异或;数据分组被分成左半部分和右半部分。左半部分与右半部分相异或构成新的右半部分,左半部分和新的右半部分运行n轮,在每一轮中,右半部分与16位密钥混合,然后与左半部分异或,从而构成新的右半部分,在N轮之后,左部分再次与右半部分异或构成新的右半部分,然后左右部分被连接起来构成全64位。这个数据分组与密钥的另外64位相异或,算法结束。
解密算法为其逆过程,加解密所用的密钥是由64位主密钥K经过子密钥生成算法产生的N+8个各为两节字的子密钥K0—Kn+8,其子密钥产生如下图所示:

FEAL子密钥生成流程图
流程简述:
首先,将64位密钥分成两部分,这两部分异或,并通过图中的函数fk进行计算,两个32位的输入被分成8位的分组,然后进行混合和代替,而后,16位密钥分组就可用于加密解密算法中。
提高FEAL加密算法密文与明文间比特依赖的方法
传统的密码安全分析观点认为:每位密文与对明文的有效依赖性越强,则加密方案的保密性愈强,提高FEAL算法的安全性,就要使得密文与更多位的明文存在依赖性。
1、采用S函数的变形函数S',在FEAL算法中,S函数为循环左移2位,可使S函数的变形函数S'为环左移1位,即为S'(X1,X2,δ)=rot(ω),其中X1,X2, δ, ω与其在S画数中的含义一致。
在使用S'后,FEAL-4输出的每位密文位只与明文的半数位有比特间依赖性,而FEAL-16,FEAL-32,FEAL64等就可使输出的每位密文位与所有明文位产生比特依赖性。使用修改S'函数这一方法不增加FEAL算法重复迭代次数,在占用机器时间上,修改后的S'比原算法中的S占用更少。这只对FEAL-16,FEAL-32, FEAL-64等有效,而对FEAL-4,FEAL-8必须同时增加迭代次数,也就相应地降低了連度。故此修改适于N大于或等于16的 FEAL-N算法,且不影响FEAL加密算法的快速性。
2、增加奇、偶位变换操作。可在每4次迭代重复时,使每个密文位与每个明文位产生比特依赖性。对FEAL-16而言,只需增加条Ri循环左移一位指令,即rot1(R).FEAL32,FEAL64分别要增加3条7条rot1(R)指令,CPU处理一条rot1(Ri)只占用2个时钟周期,故此变换操作对FEAL加密算法的速度影响甚小,只是对FEAL-4,FEAL-8无效。




