早在16世纪法国维吉尼亚就发明了“维吉尼亚加密算法”,其特点为:
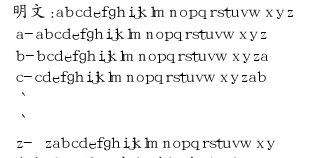
维吉尼亚加密引入密钥的概念,如对the way here加密,采用best位密钥,加密过程如:
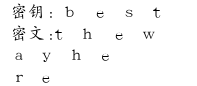
t取b行t所对应的字母为:s而h取e行h对应的字母f,以此类推,将加密后的文件传输给指定的人,并给他加密所用的密钥,对方解密就可读取文件。但不久,维吉尼亚加密算法被破解,为此很多人继续研究,写出来了各种各样的加密算法。
比如下面这样的全新的二维加密算法,我们从维吉尼亚加密中可以看出,其总共只有26根密码条(从a到z)二位加密:

(从aa~zz共26*26根密码条,每根密码条第一个字母与密码条名的第一个字母相同,如密码条名为ba-的密码条中第一个字母为b,接着为c,d,e,f,g,h….a)
密钥形式:如:b e s t
j----
g----
f----
在每个“-”填入信息,易知道其周期为12,也就是说每隔12个字母的字母在加密时密钥相同,这个思想与维吉尼亚加密算法完全一样,但是这仅仅是二维加密的简单形式,我们可以对其进行扩展。
扩展1:密钥每加密完周期个信息字母时,密钥个字母换成其后面的字母,如密钥best*jgf,加密完12个字母后变成cfto*khg,再对接着的12个信息字母,然后密钥再像这样变。
扩展2:当加密第n周期的12个字母时,每根密码条的第一个字母为其后面的第n个字母(也可以引入函数,第f(n)个字母,函数由加密和解密双方默认)以上的2个扩展方向我们分别把密钥和密码条的字母排序改变,虽然看起来只有这么简单,但是如果采用更复杂的定义,第三方就几乎无法破解被加密的信息了,再二位加密中我们可以看出,密钥就像一个矩形,矩形的相邻两边是密钥,矩形内部填充被加密的信息,通过复杂的对密钥定义和对密码条定义,我们可以编写出各种各样的加密形式,假如密码条是有加密和解密双方早就定义好的排列形式,那么第三方破解加密信息的概率简直就是0。
以上二维加密算法的形式就像一个矩形,同样我们可以用立方体的形式对信息加密,这就是三维加密算法,在一个立方体中,我们可以将密钥写在共用一个定点的三个边长上,立方体内部填充信息,某个信息字母加密时采用与其长、宽、高相等所对应的各字母组成的密码条名的那根密码条。我们也可以将密钥填充在立方体相邻的三个面上,立方体内部填充信息字母,某个信息字母加密时采用该字母向三个面投影所得的三个字母组成的密码条名的那根密码条,为了更复杂的加密,同样也可以像二维加密算法一样对三维加密算法的密钥和密码条字母的排序采取各种各样的定义从而是加密变得更复杂。
我们可以根据不同的情况的需要向四维加密算法研究,至于加密采取什么样的模型,那要看个人的爱好而定,总之,N维加密算法的引进,使加密算法有了个理论体系,在这个理论体系下,我们可以将加密算法向不通的方向进行,N维加密算法统一了各种加密算法的混乱局面,以后对信息加密根据对信息安全度的要求,我们可以在那2个扩展方向理论下开发出各种复杂的加密算法。










