带你玩转RSA加密算法

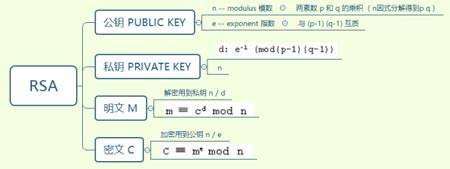
RSA是一种非对称加密算法，它由 公钥（n/e），私钥(n/d)，明文M和密文C组成。我们做CTF题目时，一般题目中会给出公钥和密文让我们推出对应的私钥或者明文。RSA的相关公式都写在上面脑图中，在正式讲解RSA加密算法前我们先来普及一波数学的基本知识。

一、相关数学基础

1.1素数和互质数

素数也称质数，它的定义为除本身和 1 的乘积外，不能表示其他数的乘积。比如2，3，5，7，11，13，17……等都是素数。
互素数也称互质数，定义是公约数只有1的两个自然数，如：
1和任何自然数 1 & 2
任意 2个质数 2 & 3
相邻2个自然数 4 & 5
3 & 10 、7 & 10 、5 & 26等等

1.2模指数运算

模运算就是取余数，如5 mod 3 =2。而模指数就是，先做指数运算在做mod运算。
如：53 mod 7 = 125 mod 7 =6
我们可以使用python的pow()来求解模指数运算。

1.3同余运算

两个整数a,b，它们除以整数M所得的余数相等：a ≡ b(mod m)，比如说5除3余数为2，11除3余数也为2，于是可写成11 ≡ 5(mod 3)。

二、RSA加密算法

2.1 加解密算法

前面已经说过，RSA是一种非对称加密算法，这个算法的特点就是明文使用公钥进行加密得到密文，而密文解密使用私钥来解。

所需的密钥对为n,d,e。密钥对是如何生成的？

2.2生成密钥对

密钥对的生成步骤如下：n  Led （L作为生成过程中的中间数）

cc普通用户

海报分享