基于混沌的数字图像加密算法
目前混沌系统与加密技术相结合是现如今最热门的一个课题,虽然有大量的加密算法面世,但是这些加密算法并不成熟,仍然需要进一步的研究。本文采用像素位置置乱变换和像素值替代变换相结合的加密思想,设计出一种基于混沌的数字图像加密算法。引入了整数域上的逆仿射变换,算法中采用二维 logistic 混沌映射相结合的方法,生成多组混沌序列,像素置乱变换与灰度值替换都由这些混沌序列所控制。多混沌序列产生的密钥空间大于单一的混沌序列所产生的密钥空间,因此本文研究的算法加密强度很高。
1. 虫口模型—Logistic混沌映射。
Logistic映射是一种可产生的非线性系统,其模型如下所示:

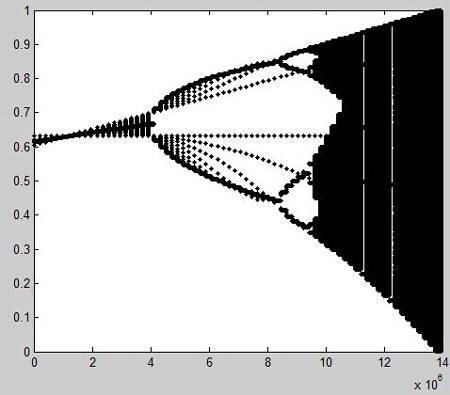
clear all clc m(1)=0.632; N=196601; m1=[]; for u1=2.6:0.02:4 for i=1:N-1 m(i+1)=u1*m(i)*(1-m(i)); end m1=[m1 m]; end plot(m1,'k.')
2. 像素灰度值替代设计图像加密
设图像(i,j)处的灰度值为 I(i,j),满足 1≤i≤M、1≤j≤N,I′(i,j)表示替换后 I(i,j)在(i,j)处的灰度值。本文中,像素值的替代变换是在空域中进行的,我们设计了两种思路用于实现混沌序列与像素值的替换操作。
像素替换的公式如下:
I′(i,j)=((r1(i,j)⊕I(i,j)⊕r2(i,j)+L−r3(ij)))modL)mod256
式中:L表示图像的颜色深度;mod表示求模运算;⊕表示按位异或运算。r1,r2,r3表示的是混沌序列值,替换变换的密钥由r1,r2,r3对应的混沌系统提供,变换可多次进行,如此加密效果更好。设重复次数为n,与混沌模型的初值和参数共同作为这一部分的密钥,增大了密钥的空间,提高了加密强度。若图像很大时,通过上式能够看出r1,r2,r3模版矩阵需要随之增大,如此就大大减小了加密效率。为此,我们可以通过分块处理的方式对图像进行加密,加密效率明显提高。原始图像和加密后的图像:

jiami.m
function e=jiami(x,data) m(1)=data(1); m1(1)=data(2); m2(1)=data(3); [a,b]=size(x); N=a*b; u1=data(4); %u=4; for i=1:N-1 m(i+1)=u1*m(i)*(1-m(i)); end m=mode(255*m,256); m=uint8(m); u2=data(5); for i=1:N-1 m1(i+1)=u2*m1(i)*(1-m1(i)); end m1=mode(255*m1,256); m1=uint8(m1); u3=data(6); for i=1:N-1 m2(i+1)=u3*m2(i)*(1-m2(i)); end sigma=data(7); m2=mode(255*m2,256); m2=uint8(m2); %n=1; n=data(8); x=double(x); m=double(m); m1=double(m1); m2=double(m2); for i=1:a for j=1:b e(i,j)=m(n)+m1(n); e(i,j)=bitxor(e(i,j),m2(n)); e(i,j)=e(i,j)+x(i,j); e(i,j)=mod(e(i,j),255); nn=n+1; end end
main.m
x=imread('lena.png'); x=double(x(:,:,1)); r=input('请输入加密密钥key1:'); e=jiami(x,r); subplot(121); imshow(x,[]); title('原始图像'); subplot(122); imshow(e,[]); title('加密图像');
密钥为[0.343 0.432 0.63 3.769 3.82 3.85 0.1 1]八位
3. 加密图像解密
解密是加密的逆,公式如下:
I(i,j)=(r1(i,j)⊕(I′(i,j)+r3(i,j))modL)⊕r2(i,j))mod256
jiemi1.m
function kk=jiemi1(e,data) e=double(e); [a,b]=size(e); e=floor(e); m3(1)=data(1); m4(1)=data(2); m5(1)=data(3); u1=data(4); N=a*b; for i=1:N-1 m3(i+1)=u1*m3(i)*(1-m3(i)); end m3=mode(255*m3,256); m3=uint8(m3); u2=data(5); for i=1:N-1 m4(i+1)=u2*m4(i)*(1-m4(i)); end m4=mode(255*m4,256); m4=uint8(m4); u3=data(6); for i=1:N-1 m5(i+1)=u3*m5(i)*(1-m5(i)); end m5=mode(255*m5,256); m5=uint8(m5); sigma=data(7); n=data(8); m3=double(m3); m4=double(m4); m5=double(m5); for i=1:a for j=1:b kk(i,j)=m3(n)+m4(n); kk(i,j)=bitxor(kk(i,j),m5(n)); kk(i,j)=e(i,j)-kk(i,j); kk(i,j)=mod(kk(i,j),255); nn=n+1; end end
函数调用形式
kk=jiemi1(e,r);
%e为加密图像,r为密钥,为8位
解密过程:

由图可以知道,错误的密钥是解密错误的,只有正确的密钥才能解密出原始图像,而且密钥的精确度非常高,能到小数点后几位。










