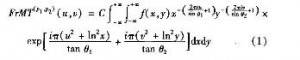密码系统设计的一个基本准则是尽量引入非线性操作来增强系统的安全性,分数梅林变换是输入函数在对数一极坐标下的FrMT,其变换具有非线性。利用线性同余伪随机序列发生器参数的敏感性,生成实对称随机矩阵随机化离散FrMT的核矩阵。在保持FrMT非线性属性的基础上,与FrMT相比,随机FrMT的密钥灵敏度大幅改善,对于是指输入的图形,便于密文的存储与传输。
图像加密算法
分数梅林变换:
二维函数f(x,y)的分数梅林变换定义为:
其中:C为常数,P1,P2分别为x,y方向的变换阶次。分数梅林变换的一种快速实现方法是将f(x,y)由笛卡尔坐标系转换到对数一级坐标中,再对转换结果实施FrMT,即
对数一级坐标变换定义如下:
对数一级坐标变换决定了分数梅林变换具有非线性属性。
数字图像加密过程
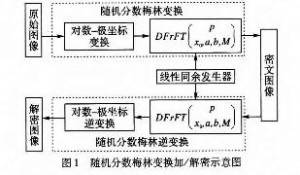
根据式(2)的类推,FrMT的实现可以在离散分数傅立叶变换的基础上得到。图像的加密和解密过程如图一所示。
待加密的二维数字图像A的FrMT的矩形形式为
其中:T表示矩阵转换,p是FrMT的分数阶。变换矩阵为
Hp=VDpVr(5)
其中V为本征向量矩阵,Dp为FrMT的本值的对角矩阵,引入LCG随机化本征向量V,即随机化了FrMT的核矩阵,LCG的递推关系为:
利用LCG生成的伪随机序列号,重构一个2维随机矩阵R,并通过计算得到一个实数对称矩阵S:
数值计算矩阵S的归一化本征向量,得到实数的本征向量矩阵V,S是对称的随机矩阵,由它计算得到的本征向量矩阵相互正交,且具有随机性。矩阵S与H满足乘积交换关系,他们具有相同的本质向量;随机话的V作为1的本征向量矩阵,也即随机化了FrMT的核矩阵,从而得到随机FrMT。随机FrMT 有FrMT良好的数学性质,且具有变换普能量均匀分布和半周几实数化的特点,则会对图像加密来说十分有益。
原始图像通过由对数一级坐标变换和随机FrMT构造的随机FrMT,完成图像素指和位置的双重加密。得到白噪声的密文。对于实值输入信号。随机分数傅立叶变换的输入结果是实值的,可节省密文的存储空间,减轻传输负担。密文的解密过程通过FrMT的逆转换完成。