针对现有基于混沌的医学图像加密算法的鲁棒性和效率不足,我们提出了一种基于快速混沌置乱的鲁棒型医学图像加密算法RMIEF-CS。
一、基于多混沌系统的序列生成算法
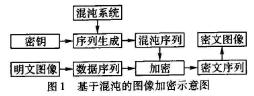
基于混沌的图像加密方法原理如图1所示,根据选定的密钥和混沌系统生成具有混沌特性的伪随机序列,然后与明文图像的数据流进行某种操作得到密文数据,并最终转换为密文图像。从图l中可以看出,混沌加密算法的加密密钥取决于生成的混沌序列,混沌序列与选取的混沌系统直接相关。虽然混沌序列在理论上是一个无限的伪随机序列,但在计算机中实现时通常由于计算机有限的精度而造成混沌收敛问题,即混沌序列在迭代的过程中呈现周期性,这让攻击者有机会破解混沌序列。为了有效缓解混沌收敛的问题,有研究者们提出了自己的方法,如Logistic函数迭代过程中进行大整数化的方法以解决有限精度问题;如在Logistic函数中引入反正弦与反余弦变换,对Logistic映射进行优化改进。
上述方法虽然在一定程度上缓解了混沌有限精度问题,但计算过程较为复杂,或者只针对同一混沌系统进行,灵活性不足,特别是针对高安全性和高容量的医学图像加密时有着明显不足。本文提出一种基于多混沌系统的混沌序列生成算法,在有效缓解有限精度问题的同时保证产生的混沌序列具有足够高的复杂度,在应用于医学图像加密时具有较高的安全性和运行效率。
1、混沌系统选取
除了考虑混沌序列的“有限精度”问题外,医学图像数据量大,加密的时间效率必须在可接受的范围内,综上,算法选择使用多个低维的混沌系统协同工作产生混沌序列。选取的一维混沌系统如下:
1) Loejstic映射:
Logistic映射函数如式(1)所示:
![]()
其中:X∈(O,1),当u∈(3. 5699456,4)并且X≠l-U-1时系统处于混沌状态。
2)分段线性混沌映射(Piecewise Linear Chaotic Map,PLCM):
PLCM映射函数如式(2)所示:
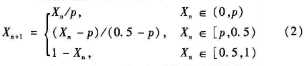
当xn∈(O,1),p∈(0,0.5)时,系统处于混沌状态。
由于低维混沌系统产生的序列复杂性稍低,并且存在混沌收敛问题,本文算法将采用的两个低维混沌系统得到的序列进行处理,使两个混沌系统在算法产生序列的过程中相互作用,通过在混沌系统间随机切换交替产生混沌序列,以加大遭受相重构攻击破解的难度,同时很好地缓解混沌收敛问题。
2、混沌序列生成
序列产生过程中,为了避免同一个混沌系统产生过长的序列降低整体混沌序列的复杂度,对两个混沌系统产生的序列长度进行限制,设为LENmax。考虑到混沌系统产生的初始序列混沌特性不强,在选取混沌序列时让混沌系统先进行NUM次迭代。具体的混沌序列生成过程如下:
1)将医学图像转换为二进制数据流,得到加密所需的混沌序列的长度CS_LEN。
2)随机选取i的值,其中i∈{l,2}。
3)利用第i个混沌系统进行一次迭代产生混沌数值sa,则第j(j=i mod 2+1)个混沌系统要产生的混沌序列的长度s一Len可用式(3)计算所得:
![]()
其中N为常数(取10 000),用来放大sa。
4)CS_LEN=CS LEN - S_Len,如果CS LEN≤0,则令S_Len=CS_LEN,利用第_『个混沌系统产生长度为S_Len的混沌序列,序列生成结束,转第6)步执行。
5)如果CS LEN>0,令Z=l mod 2+l,转第3)步继续执行。
6)返回产生的混沌序列。
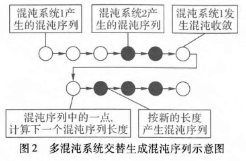
图2给出了两个混沌系统相互交替生成混沌序列的示意图,从图中可以看出,混沌序列的产生由两个混沌系统共同作用,每个系统的序列长度由上一个系统产生的混沌数值决定,由于存在着混沌系统间相互的随机切换,增加了混沌序列的复杂性,大大增加了遭受相空间重构攻击破解的难度;同时,即使产生序列的过程中某个混沌系统发生了混沌收敛问题进人周期循环,只要两个系统不在同一时间达到周期点,那么整个系统产生的混沌序列则不会进入周期循环。本文算法产生的混沌序列能很好地满足大数据量的医学图像加密。
二、RMIEF-CS算法
1、密文反馈机制
为了提高加密算法的安全性,在加密过程中引入密文反馈机制,本文使用的密文反馈机制如图3所示。
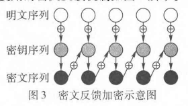
同时,为了避免单向的反馈机制使得第一个像素点或者最后一个像素点得不到反馈作用,引入双向密文反馈方式。设D为图像明文数据流,E为加密序列,则正向反馈可以描述为式(4)和(5),反向反馈可以描述为式(6)和(7)。
对于第一个图像数据:
![]()
对于之后的图像数据:
![]()
对于非最后一个图像数据:
![]()
对于最后一个图像数据:
![]()
密文反馈加密可以将加密过程中的变化不断进行传输,影响变化点前后的加密操作,使算法具有良好的雪崩效应;另外针对医学图像具有大片连续相同像素区域的特点,反馈机制能将微小的变化无限扩大并扩散,增加加密效果和算法的安全性。
2、置乱加密算法
RMIEF-CS加密算法大致过程为:先获取明文数据流,然后根据所介绍的混沌序列生成方法得到密钥,根据密钥对明文数据流进行置乱;再次得到新的混沌序列,对中间的置乱结果引入双向密文反馈机制进行再次置乱,最终得到密文数据。具体的置乱加密算法如下所示:
1)读取待加密图像;
2)将I转换为明文数据流D;其长度为N;
3)计算加密序列长度CS_LEN=N*T,set T=3;
4)设定混沌系统的密钥,并初始化相关参数LENmax=300,NUM=100.i=l;
5)利用混沌序列生成算法得到长度为CS_LEN的序列CS1;
6)调整Csl为字节序列BS,,BSi (i)=(CSi (i)*10n)mod256,setn=5;
7)setk=0;
8)while(k<CS_LEN){
9)D(BS1(k))↔D( BSi(k+l));//交换
10)k=k+l;
11)set i=2,重新生成长度为Ⅳ的序列CS7;
12)调整CS2为字节序列BS2,BSz(i)=(CS2 (i)*105)mod 256;
13)利用BS2对数据流D进行双向密文反馈得到密文数据流ED;
14)将ED转换为密文图像输出。
三、 实验结果与讨论
实验中采用的硬件环境为Windows XP SP3,CPU为Intel Pentium CPU E7500 2.93 GHz,内存1.92 GB;采用Microsoft Visual Studi0 2005平台中的VC++语言实现本文算法。为了保证数据的有效性,从某大学医学院数据中心获取了100多幅不同形态的医学图像进行实验,均得到了较好的加密效果,限于篇幅以一幅1024 x1024的24位MRI灰度图像的测试结果进行说明。图4给出了原始医学图像和其加密效果图。
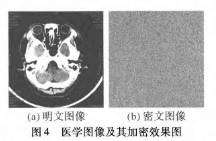
从图4可以看出,图像经过加密之后呈现杂乱无章的噪声图像,看不出任何原始图像的轮廓信息,图5给出了本文方法产生的混沌序列的性能分析,相应的参数设置为Logistic混沌系统中的x=0.36,u=3.92;PLCM映射中的y=0.55,p=0. 23,LENmax=300,NUM=100。图5(a)为从混沌序列的第101次迭代连续取的99个值画出的分布图,图5(b)是在修改混沌参数p=0. 23+10-16时(其他参数保持不变)的混沌值分布图。从图5中可以看出,虽然只是对参数进行了极其细微的修改,得到的混沌序列却截然不同,说明混沌系统对初值具有极度敏感性。虽然由于计算机精度有限会带来混沌收敛的问题,但本文方法的多混沌系统交替产生序列的方法能较好地避免周期现象的产生。两个混沌系统一共有4个敏感性参数作为密钥,对于攻击者来说实施暴力破解的难度是非常大的。
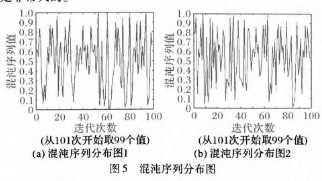
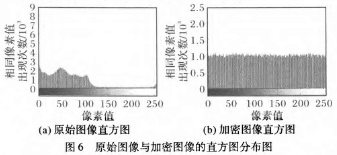
图6给出了原始图像和加密图像像素灰度值分布直方图,从图6(a)中可以看到医学图像的分布特点是像素分布不均匀,绝大部分像素出现在极值点附近,容易受到统计攻击。好的加密算法应该使图像的直方图越均匀越好,从图6(b)中可以看出,本文的加密算法具有较好的性能。
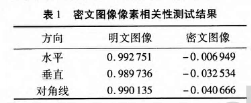
医学图像的特点之一就是相邻像素的相关性强,利用式(8)计算图像像素的相关性:
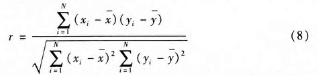
其中:N为实验中进行对比的像素对总数;xi、yi分别为两组像素中的像素值;x和y为两组像素的平均值。实验中随机选取了密文图像中水平、垂直和对角线上的3000个像素对进行统计,其结果如表1所示。从表l中可以看出,RMIEF-CS能较好地消去医学图像相邻像素间的相关性。
同时,经过测试,RMIEF-CS算法具有较好的明文敏感性,修改明文中的任一像素点均会造成得到的加密图像相似度非常低,即具有较好的雪崩效应。
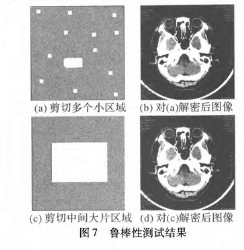
为了测试RMIEF-CS算法的鲁棒性,实验中对密文图像进行了不同程度的修改,如图7所示。从图7中可以看出,当对密文图像进行小尺寸的剪切操作时,解密出来的图像基本和原始图像一致;当剪切的区域较大时,解密出来的图像虽然具有较明显的噪声现象,但仍具有原始图像的基本轮廓。RMIEF-CS算法的鲁棒性实际上通过图像置乱实现,由于密文图像经过随机置乱形成,当密文图像因为各种原因受损时,在解密的过程中,受损的部分也会随机分布到原图的各个部分,从而保证了图像的大致轮廓能识别出来。
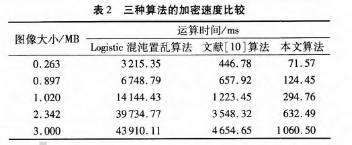
最后,将RMIEF-CS算法的时间效率与现有的方法进行了比较,其中一个比较对象是使用Logistic混沌系统生成混沌序列,然后将序列进行排序后对图像进行置乱;综合运用Arnold和Logistic混沌系统对图像进行置乱。比较结果如表2所示。
MRI也就是磁共振成像,英文全称是:Magnetic Resonance Imaging。





