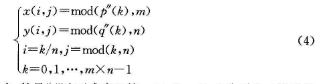通常的彩色图像加密算法未能充分考虑RGB各颜色分量之间的内在联系,抵抗统计分析能力不强。为进一步增强图像置乱程度与加密安全性,在结合混沌置乱的基础上,我们提出了一种新的彩色图像加密算法。
一、logistic混沌映射系统
混沌是一种非线性无规则的运动,是在确定性非线性系统中不需附加任何随机因素也可出现的一种内在随机性,因此其伪随机行为能够准确再生。如一维logistic映射从数学形式上来看是一个非常简单的混沌映射,该类系统具有极其复杂的动力学行为,其数学表达式如下:
当μ∈[3.56994567,...,4],xk∈(0,1)时,logistic映射呈现混沌态。
混沌系统的这些特性与密码学要求的扩散、置乱和随机特性相吻合,在保密通信领域的应用非常广泛。但部分图像加密方案采用了一维混沌系统,因此其安全性不高,由于二维logistic映射具有一维logistic映射简单的形式,又具有多维混沌系统多参数、行为复杂的特点,本文利用二维logistic映射进行图像加密处理。二维Iogistic映射的动力学方程如下:
其动力学行为是由其中的参数μ、λ1、λ2、γ来控制的,通常取μ=4。当λ1=0.9、λ2=0.9、γ=0.1时,经过计算得到二维logistic系统处于混沌状态。
二、彩色图像加密算法
为充分扰乱彩色图像RGB分量的相关性,本文提出一种基于二维混沌映射与比特随机重组的彩色图像加密算法。算法首先将RGB分量视为一个整体,以将彩色图像转换成一扩展的灰度图像,然后利用二维logistic映射优良的伪随机特性与行为高复杂性,对彩色图像进行位置置乱,并结合比特异或与随机重组进行像素扩散。
1、基于二维logistic映射的像素位置置乱
基于2D logisitc映射的彩色图像位置置乱过程描述如下:
步骤1读人大小为m×n的彩色图像I。
步骤2初始化logistic映射控制参数:μ=4。当λ1=0.9、λ2=0.9、γ=0.1,并初始迭代映射:ko =300,给定密钥key1={x0,Yo},其中x0、Yo为混沌映射的两个初始值。
步骤3以密钥key,为初始值,由式(2)迭代映射m×n十ko次,生成优×n+ko对混沌序列值,舍弃ko对值,得到mXn对的混沌序列值,并将其分别存储于大小为辨×n的一维数组P和Q中。
步骤4对P和Q中的元素做如下运算:
得到两个整数数组P'、Q'。
步骤5通过对数组P’、Q',进行排序以生成两个长度为m×n的一维伪随机序列P"、q'',其元素值取[o,m×n一1]内不等的整数。
步骤6对一维随机序列P"、q''中的各元素P"(k)、q''(k)实施式(4)所示的变换,并将其映射为大小为m×纸的二维置乱矩阵X、y。
式中,符号"/”表示求商运算,x(i,j)、y(i,j)分别为二维置乱矩阵X、y的元素。
步骤7利用置乱矩阵X、y对图像J进行位置置乱,得到置乱图像数据I'。
2、结合比特异或与随机重组的像素值变换
图像置乱破坏了图像原像素的相邻像素点的相关性,但是像素点的灰度值并没有改变,即图像直方图并没有改变。为降低RGB各分量间的相关性,进一步利用异或操作与10-gisuc混沌映射对置乱后的扩展的图像数据I'进行灰度变换,以提高加密效果,具体由以下几个步骤构成。
步骤1 对置乱图像,各像素RGB分量进行以下异或操作,得到异或后各像素的R'G'B'分量。
步骤2将异或后RGB分量组装成一个24比特的整体,于是彩色图像被扩展为一幅24比特的扩展灰度图像。
步骤3给定密钥key2,以key2为初始值,利用式(1)生成混沌序列S,且其元素值取[O,23]内不等的整数。
步骤4利用混沌序列S对扩展灰度图像各24比特像素值进行随机置乱,再将置乱后的24比特像素依次重新组装成新的RGB分量。
步骤5重复以上步骤,直到所有像素处理完毕,即得到加密彩色图像I''。
3、解密算法
解密过程是加密过程的逆过程,只需给定相同的混沌系统密钥即可,主要由以下几步完成。
步骤1给定与加密过程相同的密钥key1、key2,与加密过程相同,由密钥keyi生成置乱矩阵X、y。
步骤2由置乱矩阵X、y对加密彩色图像I'进行像素位置逆置乱,得中间图像i。
步骤3对中间图像I的各R'G'B'分量实施如式(6)所示的异或操作,并将其组装成一个24比特的整体,得到扩展的24比特扩展灰度图像。
步骤5重复以上步骤,直到所有像素处理完毕,即得到解密彩色图像I。
三、仿真实验与性能分析
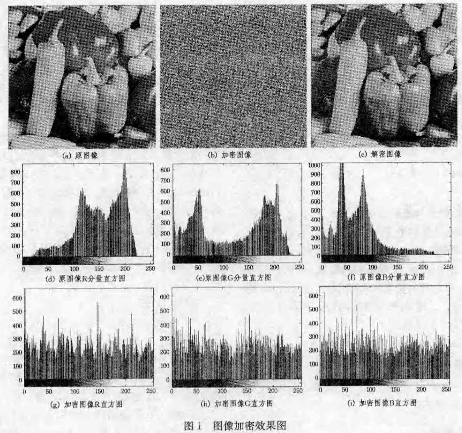
实验中选取大量大小为256×256的RGB彩色图像进行测试,图1以peppers图像为例给出了算法加密效果图,给出了加密前后的图像直方图,加密后图像的灰度直方图变化较大,其灰度分布比较平坦,同时人眼从加密图像(见图1(b))中也难以察觉出原始图像的任何信息,这说明加密图像有较好的视觉加密效果。
1、密钥空间分析
—个良好的加密方案应有足够大的密钥空间以挫败穷举攻击。本文基于彩色图加密算法中以二维logistic混沌系统的初始值ke1和一维logistic混沌初始值key2为密钥,若精度为10 -16,则该加密算法密钥空间可达1048,密钥空间足够大,可以有效阻止各种暴力攻击试图。
2、密钥敏感性分析
以图l(b)的加密图像为例,图2给出了密钥微小变化时的解密仿真实验结果,其中图2(a)和图2(b)分别是密钥key1和key2最后一位有效数字不同时的解密图像。由图2可见,即使密钥keyi和keyz有微小的变化,也会生成完全不同的加密图像。由此可知,该加密算法中任何一个密钥即使存在很细小的改变,也不能正确解密图像,这正是logistic混沌系统对初值的敏感性所致。
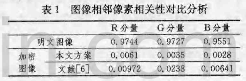
3、相邻像素相关性
以lena图像为例,从原图像和加密图像中分别随机选取2000对相邻像素,计算其相关性,测试对比,实验结果如表1所列。从表1中可以发现,原始明文图像相邻像索的相关性很强,而加密图像相邻像素相关性很低,几近于0。
小知识之Logistic函数
Logistic函数或Logistic曲线是一种常见的S形函数,它是皮埃尔·弗朗索瓦·韦吕勒在1844或1845年在研究它与人口增长的关系时命名的。