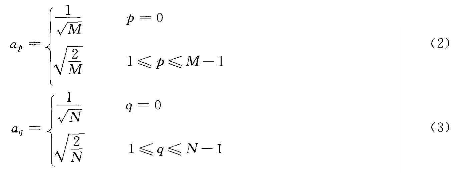彩色图像加密算法之单通道RGB分量 - 夏冰加密软件技术博客

为了保证图像在传输过程中的可靠性和安全性，针对传统多通道加密算法无法实现同步加密、传输负载大等不足，我们提出了一种基于单通道RGB分量的彩色图像加密算法。

一、单通道RGB分量

1、离散余弦变换(DCT)

离散余弦变换(Discrete Cosine Transform，DCT)是一种类似于离散傅里叶的变换方法，只适用于实数，DCT相当于一个长度大概是它2倍的离散傅里叶变换。DCT的特点：图像经DCT变换后，数值大的频谱系数主要集中在DCT系数比较小的范围，且其主要分布在频谱较小的左上角区域，这说明有用信息有集中区域，设一幅图像的大小为M×N，则DCT定义为：

式中，Bp,q称为矩阵A的DCT系数，m=0, 1, ... , M-1; n=0, 1, ... , N-1; p== 0, 1, ... , M-1,q=o，1，…，N-1; ap，aq分别定义如下：

2、离散余弦逆变换

离散余弦逆变换(IDCT)是DCT的一种可逆变换，利用IDCT可获得与原始图像相近的重建图像，重建图像与原图像存在一定的差异，但重要的信息都被保存了下来，离散余弦逆变换定义为：

式中，Bp,q称为矩阵A的IDCT系数。

3、ZigZag置换

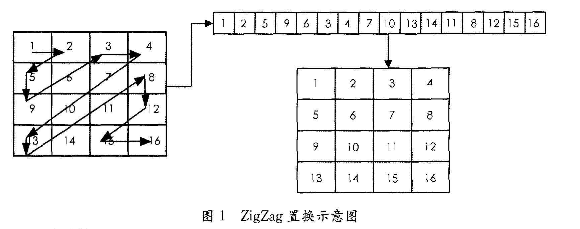
ZigZag置换具有实现简单，时间复杂度低等优点．ZigZag置换首先将扫描到的元素依次存放到—个一维数组中，然后再将此一维数组按一定的方式置换为二维矩阵，具体如图1所示。在数据传输和加密过程中，ZigZag置换可以描述为：设明文为一维数据C，采用一定的扫描顺序和放人顺序，得到密文数据C'，重复上述过程直到满足指定的迭代次数。

4、Logistic混沌映射

Logistic混沌映射是一种运算简单、应用广泛的一维离散时间非线性动力系统，可以快速产生混沌序列的时间，简化密钥流的产生过程，提高密钥生成效率。Logistic混沌映射的方程表达如下：

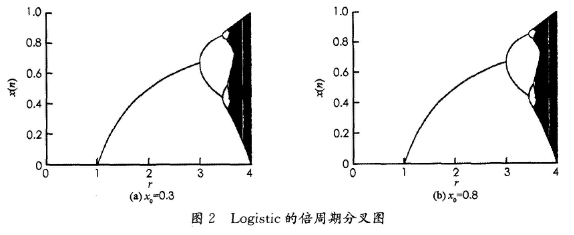
其中，xn是系统的状态变量；μ∈[O，4]是Logistic混沌映射的分岔参数，图2分别画出了x0=0.3，x0=0.8时Logistic映射的倍周期分叉图，从图2可知，x0取(0，1)区间内的任意值，Logistic映射均能够进入混沌状态。

二、本文彩色图像加密算法

1、工作原理

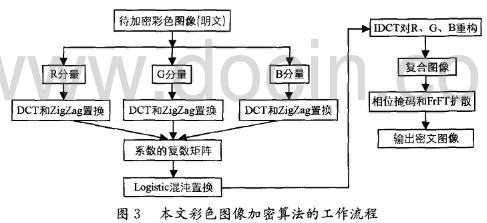
本文彩色图像加密算法的工作原理为：首先提取大小为M×N的明文RGB彩色图像的RGB 3个分量，并对它们进行离散余弦变换和ZigZag置换，产生复数矩阵；然后采用Logistic混沌映射对图像进行混沌置乱；最后采用混沌掩码和分数傅里叶变换(Fractional Fourier Transform，FrFT)对复合图像进行扩散，得到加密图像，具体工作流程如图3所示。

2、彩色图像加密算法的工作步骤

1)设待加密彩色图像I大小为M×N，分别提取它的RGB 3个分量）。

2)将彩色图像I分成多个大小一致的子块，然后通过离散余弦变换即式(1)对每一个子块进行变换，得到彩色图像I的系数矩阵IR，IG，IB。

3)采用ZigZag置换技术分别对IR，Ic，五矩阵进行扫描，实现矩阵中元素的置换，产生矩阵HR，HG，HB，并根据式(6)的迭代方式产生系数的复数矩阵。

其中Mi代表第i次迭代的复数矩阵；M代表复数参量．

4)通过Logistic映射产生随机序列x=（xl，X2，…，菇撸），并采用该随机序列对Mi、HB的位置进行置乱，具体如下：

5)采用离散余弦逆变换即式(3)对系数复合矩阵肱进行重构，产生第一次复合图像I'

6)输入初始值x0，根据式(5)产生Logistic混沌的相位掩码，并结合分数阶傅里叶变换，形成正则函数LCT：

其中，f(x，y)为复合图像I'；λ为一个常量。

7)根据相位掩码和正则函数LCT对复合图像，I'进行扩散，产生最终密文图像，I''，加密函数具体如下：

三、仿真实验

1、仿真环境

为了测试本文彩色图像加密算法的性能，在Intel酷睿2.85 GHz CPU，4 GRAM，Windows XP操作系统的个人计算机上，采用编程工具Maltab R2012进行仿真实验，采用标准测试图像lenna(256×256)作为仿真对象，具体如图4(a)所示，对其进行4×4大小的不重叠分块操作。

2、算法的实现

首先对图4(a)中的彩色图像lenna的RGB 3个彩色分量进行提取，结果如图4(b)～(d)所示，然后采用DCT分别对它们进行变换，得到彩色图像的系数矩阵如表1所示，最后采用上述步骤得到加密后的图像。

3、本文算法的性能分析

1）直方图分析

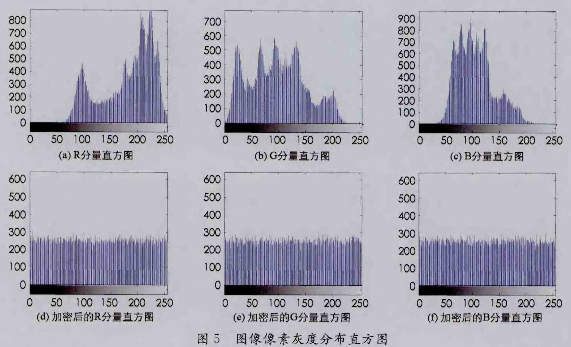
像素点的分布状况可通过直方图进行描述。图5(a)，(b)，(c)为原始图像像素的直方图，5(d)，(e)，(f)为本文算法加密后的直方图．从图5(a)，(b)，(c)可知，原始图像的像素点灰度分布极不均匀，波动范围比较大，这表明它们的伪随机性不高，很容易被攻击和破译；而从图5(d)，(e)，(f)可知，经过本文算法加密后的图像灰度直方图产生了根本性变化，像素点分布非常均匀，有效掩盖了原始图像各像素的分布情况，使攻击者通过直方图无法获取原始图像信息，拥有较高的抗统计分析攻击能力。

2）鲁棒性分析

首先利用算法对Lenna图像进行加密，然后对加密图像进行一定程度的剪切，最后对剪切图像进行解密，结果如图6所示，从图6可知，即使图像受到50%剪切，解密算法仍然能够恢复出原始图像，说明本文算法可有效抗剪切攻击，这主要由于本文加密算法可以保证被剪切掉部分具有最大的不相关性，从而可以很容易地恢复原始图像。

在加密后图像中加入均值为0，方差为6的高斯白噪声．图7为加入不同程度的高斯白噪声的加密图像与解密图像，其中第1排为加密图像，第2排为解密图像。从图7可知，当加密图像受到不同程度的高斯白噪声影响时，本文图像解密算法能基本恢复出原始图像，而且基本不会影响图像整体视觉效果，结果表明本文加密算法可以抵抗不同程度的高斯白噪声攻击，具有较强的鲁棒性。