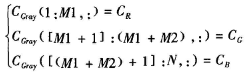针对当前彩色图像加密算法都是对RGB分量中所有像素加密,无法避免对次要像素的加密,使其加密效率较低,且加密后仍为彩色密文,增大了传输负载等不足。对此,本文提出了锯齿空间填充曲线耦合压缩感知的单通道彩图RGB分量灰度化实时同步加密算法。
一、锯齿空间填充曲线
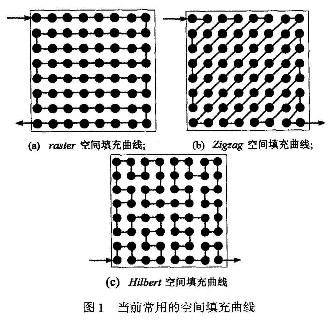
空间填充曲线是连续扫描技术,对整个图像所有像素进行遍历一次,能够有效置乱图像像素位置,主要有:raster、Zigzag以及Hilbertr,其结构见图1。raster空间填充曲线(见图l(a))虽然简单,但是该技术的置乱效果较差;而Zigzag以及Hilbert技术(见图l(b)、(c))虽然能得到较好的置乱图像,但是其结构复杂,且只能用于方形图像。
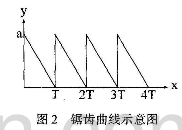
对此,有必要设计一种新的空间曲线,不仅其结构简单,还能用于矩形图像,故本文基于锯齿曲线(见图2)。
定义了锯齿空间填充曲线,见图3和图4。
锯齿曲线模型如下:
其中,a为曲线的高度,T代表曲线周期。
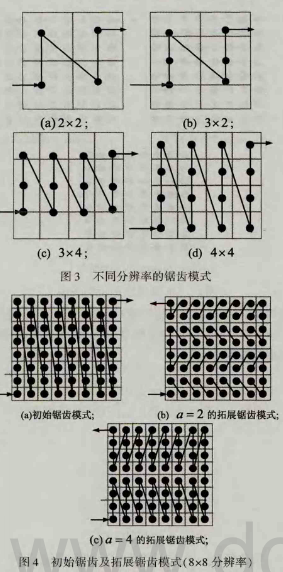
根据模型(1),定义锯齿空间填充曲线,其中,a、T则分别为图像分辨率的高度与宽度。根据图2可知,本文的锯齿空间填充曲线实质是由多个直角三角形构成。因此,锯齿空间填充曲线通过访问直角三角形上的每个点,并遍历这些点或者像素一次,完成图像置乱。不同的图像分辨率所对应的锯齿模式见图3,从图中可知,该锯齿空间填充曲线仍然可以用于矩形图像置乱。图3(a)、(b)、(c)、:(d)确保了a、T的值仅仅等于分辨率的高度与宽度。另外,还可对口强加附加条件:D的取值必须能被分辨率高度整除,根据该附加条件,来拓展原始锯齿空间填充曲线,见图4。图4(a)为初始的锯齿填充模式;而图4(b)、图4(c)代表a =2、a=4对应的拓展锯齿空间填充模式。
为了更直观的评估本文设计的锯齿空间填充曲线,利用该技术处理图5(a),结果见图5。从视觉上看,raster空间填充曲线的置乱效果不佳;而Zigzag、Hilbert以及本文的锯齿空间填充曲线的像素置乱率比较,显著打乱了图像像素位置;特别是本文设计的拓展锯齿填充曲线,在a= 32,16,8时,置乱效果较佳,能够有效破坏图像像素间的关系,可获取较佳的退化图像;而a取其他值,有部分信息泄露。故对于本文设计的锯齿空间填充曲线,取a= 32,16,8,可获得较理想的置乱图像。
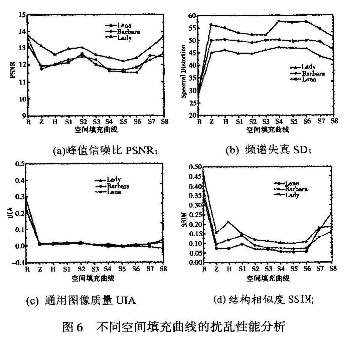
为了具体量化本文锯齿空间填充曲线与其他技术的置乱效果,本文借助峰值信噪比PSNR、频谱失真SD、通用图像质量UIA以及结构相似度SSIM来评估。令raster、Zigzag与Hilbert空间填充曲线记为R、Z、H;令本文设计的锯齿空间填充曲线分别为SI(初始)、S2(a=128拓展)、S3(a=64拓展)、S4(a=32拓展)、S5(a=16拓展)、S6(a=8拓展)、S7(a=4拓展)、S8(a=2拓展)、从图像库中择取常用的3幅图像,分别记为Lady,Lena以及Barbara为测试对象,尺寸为256×256的灰度图像,测试结果见图6。从图中可知,当a= 32,16,8,本文锯齿空间填充曲线的SD最小,SSIM最大(图6(b)、(d)),其性能要优于raster、Zigzag以及Hilbert等技术,这表明图像的置乱效果更好。
二、彩图灰度化实时加密算法设计
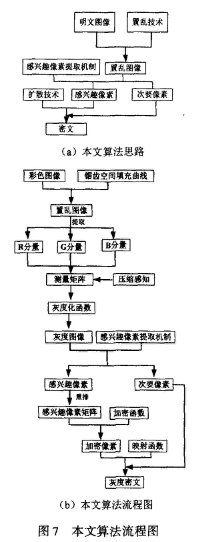
本文加密算法见图7。
从图7(a)可知,该算法为选择性加密,只扩散SP,不考虑次要像素;而当前算法是加密图像所有像素,属于全局扩散,其扩散像素数量非常大。由图7(b)可知,该算法的步骤有;
(1)基于锯齿空间填充曲线,高效扰乱彩图;
(2)根据压缩感知,对置乱感兴趣像素进行同步压缩;
(3)基于SP择取机制,形成SP矩阵;
(4)构造加密函数,获取灰度密文。
加密算法设计
(1)若彩色图像j的尺寸为NxN,利用本文设计的锯齿填充曲线,扰乱图像I,得到置乱图像I';
(2)再提取出置乱图像,7的RGB三分量,分别记为IR,IG,IB;
(3)给定密钥KR,Kc,KB,根据压缩感知,得到3个测量矩阵(PM1×m,cpM2×n,cpM3×n(g为感兴趣像素测量)。其中:
其中,M1、M2、M3分别代表彩图R、G、B分量像素矩阵行数。
(4)根据步骤(3)中的3个矩阵,测量对应的RGB三分量MR,Mc,MB,结果记为:CR,Cc,CB。
(5)根据模型(IO),可将CR,CG,CB合并成灰度图像Igray。
(6)利用SP提取方案,分离灰度图像IGruy的感兴趣像素与次要像素。
(7)由大到小,重排SP,形成SP矩阵M。
(8)构造加密函数,扩散矩阵M,得到加密矩阵M':
其中,mod为求余操作。
(9)根据位置映射,将M’映射到灰度图像矩阵M对应的位置,形成灰度密文I’:
其中:L为位置映射函数;RI'为加密像素矩阵M'中的第i个元素;ri为感兴趣像素矩阵M中的第i个元素。
压缩感知,又称压缩采样,压缩传感。它作为一个新的采样理论,它通过开发信号的稀疏特性,在远小于Nyquist 采样率的条件下,用随机采样获取信号的离散样本,然后通过非线性重建算法完美的重建信号。