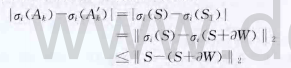Weyl定理在数字图像加密传输中的应用 - 夏冰加密软件技术博客

针对数字图像如何更好地在网络中进行安全传输的问题，需要研究一种高质量的加密和解密算法，使得加密图像以不可见隐藏方式嵌入叠加到非加密图像中，并且使得提取后的加密图像与原图像具有较好的一致性，为此，我们提出了一种基于Weyl定理的数字图像保密传输方法。

一、图像加密分析

图像是由像素组成的，图像的每一个像素都有自己的颜色、亮度和饱和度，对于一幅图像来说，可以根据其每一个像素的不同属性来描述它，从而把颜色信息量化为数值信息。对于真彩色图像，用记录红、绿、蓝三原色的三个矩阵描述。

加密图像隐藏的过程就是对非加密图像矩阵叠加加密图像信息的过程；而提取加密图像的过程，就是要从叠加有加密图像信息的矩阵中，分离出加密图像信息的过程，这里的关键问题在于信息的叠加。对于一幅图像通常用图像矩阵的范数来衡量图像的能量，根据矩阵范数的平方等于矩阵的所有奇异值的平方和可以知道图像的主要能量集中在数值较大的奇异值上。但在实际的应用中，图像总是带有一定的噪声的，也就是说待分解的图像矩阵一般都是被扰动的，因此要想建立稳定性好的模型算法就必须知道噪声对矩阵奇异值的影响。

Weyl定理：设A为一个大小为m×n的矩阵（m≥n），B=A+a，a是矩阵A的一个扰动，假设矩阵A、B的奇异值分别为σ1、σ2…σr(1)和σ1、σ2…σr(2)；σ*是矩阵B的最大奇异值。

由Weyl定理可知，当图像被施加小的扰动时图像矩阵的奇异值的变化不会超过扰动矩阵的最大奇异值，因此基于矩阵奇异值分解的图像隐藏算法具有很好的稳定性，能够有效地抵御噪声对加密图像信息的干扰。

下面即是根据矩阵奇异值的这种抗干扰能力，利用基于矩阵奇异分解的图像隐藏算法可以得到较好的合成图像的处理方法，并且提取后的加密图像与原图像具有较好的一致性。相反，提取图像时用加密图像嵌入时的逆过程就可以提取出加密图像矩阵信息。

二、图像加密模型的建立与求解

1、模型假设

1)假设图像在传输过程中图像信息不出现误码；

2)假设图像的微弱变化不影响图像的使用；

3)假设非加密图像可以在不失真的情况下被放大缩小。

2、符号说明

AK为图像①对应的矩阵；AK为图像②对应的矩阵AK'为合成图像对应的矩阵；w*为提取出的加密图像所对应的矩阵；Ak为A的某一个大小为m×娩的子块矩阵；S为Ak的奇异值矩阵；SK为嵌人加密图像AK后的新奇异值矩阵；σ1（I）为矩阵Ak的第亡个奇异值；Ak为受到干扰的图像矩阵；a为嵌入强度因子。

3、模型的建立与求解

（1）加密图像的嵌入

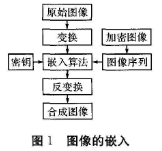
对于一幅图像来说，可以根据其每一个像素的不同属性来描述它，从而把颜色信息量化为数值信息。对于真彩色图像，用记录红、绿、蓝三原色的三个矩阵来描述。文中研究的图像都是真彩色的图像，所以其图像矩阵是三维矩阵，可以将一个三维矩阵分解为三个二维矩阵，这样我们就能充分利用图像信息进行数据处理，嵌人流程如图1所示。

非加密图像②对应的图像矩阵A为MXN，需要嵌入的加密图像①对应的图像矩阵W大小为m×n，A是是A某一个大小为m×n的子块，显然有M≥m；N>n。

文中研究的两幅图像并不是这种理想情况，所以在图像嵌入时有两种选择，一是将加密图像进行无损压缩；二是对非加密图像进行等比扩大（防止图像变形），然而实际上有用信息是加密图像，将加密图像压缩就会增加噪声的影响程度，所以必须将非加密图像等比扩大，然后得到相应的矩阵尊。

首先对A套进行奇异值分解，得到A一US Vr，其中S是A,的奇异值矩阵，目标就是将保密矩阵W嵌入到矩阵S中，在这里定义一个描述保密嵌入程度的参数a’，称为嵌入强度因子，则保密嵌入的过程表示为S7一S+aw。

可以看出，矩阵S7包含了所有保密信息，保密信息的能量反映在S7的奇异值当中。对S7进行奇异值分解，得到S7；S+ aw =U SIW，则S1反映了嵌入的加密图像全部信息，因此令S1为嵌入保密后的图像A：的新奇异值矩阵，南此可以得到嵌入保密后的图像子块A：=USi Vr，这样就完成了加密图像的嵌入。

上述保密嵌入算法的基本过程可以表示为：

在上面的公式中，矩阵U，V，U，V1都是正交矩阵。由于对一个矩阵进行正交变换后它的奇异值保持不变，因此矩阵Ak与S，ak'与S 7有相同的奇异值。设仍(A')为矩阵A。的第ak个奇异值()，通过Wey1定理可知原图像矩阵子块和嵌入加密网像矩阵子块的奇异值之间有如下关系：

上式中，嵌入强度因子a的意义在于其衡量了加密对原图像的扰动情况一在加密嵌入时，选择合适的强度因子是很重要的，小的嵌人强度因子有利于保护图像的透明性，但嵌入的加密信息容易受到外界噪声干扰，如果噪声干扰足够大，则加密信息可能被噪声淹没而完全消失，导致提取加密图像时无法得到加密图像的全部信息；大的嵌入因子有利于增加算法的稳定性，即使在噪声较强的情况下加密信息也不会受到很大影响，但是过大的嵌入强度因子可能对原矩阵的奇异值产生较大影响，有可能破坏加密图像的透明性，影响图像质量和保密性。因此，在加密嵌入时要选择适当的嵌入强度因子使保密的图像的不可察觉性与稳定性达到最佳。合成的图像如图2所示。

（2）加密图像的提取

加密图像的提取是上述嵌入过程的逆过程，通过提取可以把加密图像显示出来。在加密图像提取时我们得到的是受到干扰的图像矩阵Ak，首先对Ak进行奇异值分解：

由此得到包含有全部加密图像信息的奇异值矩阵s1*，然后利用加密图像嵌入时的矩阵U1，Vl得到：

根据上述加密图像嵌人的算法可得：

这样就得到了加密图像的信息w*，其中a为加密图像嵌入时所月j的嵌入强度因子，S为非加密图像②的奇异值矩阵a提取的图像如图3所示。

4、图像的比较和检验

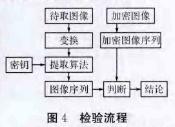
图像矩阵的元素表示图像在该像素点处的颜色强度，数值范围是从0～255。0表示该点颜色强度最低，表现在颜色上该点是黑色；255则表示该点颜色强度最高，表现在颜色上该点是白色。为了检验提取后的图像与原图像的差别并用数值表示出来，需要将提取后的图像与原图像的图像矩阵进行减法运算。减法带来的问题是负值的出现，由于图像矩阵的元素取值只能是0~255，在出现负值时矩阵的负值会自动调整为0，在取绝对值后再求矩阵所有元素的和，根据所有元素和的大小对建立模型的稳定性进行评价。检验流程如图4所示。